常见算法总结

[toc]

常见算法总结

Floyd 判圈算法

Floyd判圈算法(Floyd Cycle Detection Algorithm)，又称龟兔赛跑算法(Tortoise and Hare Algorithm)，是一个可以在有限状态机、迭代函数或者链表上判断是否存在环，求出该环的起点与长度的算法。该算法据高德纳称由美国科学家罗伯特·弗洛伊德发明，但这一算法并没有出现在罗伯特·弗洛伊德公开发表的著作中。 如果有限状态机、迭代函数或者链表上存在环，那么在某个环上以不同速度前进的2个指针必定会在某个时刻相遇。同时显然地，如果从同一个起点(即使这个起点不在某个环上)同时开始以不同速度前进的2个指针最终相遇，那么可以判定存在一个环，且可以求出二者相遇处所在的环的起点与长度。

算法描述

判断是否存在环路

如果有限状态机、迭代函数或者链表存在环，那么一定存在一个起点可以到达某个环的某处(这个起点也可以在某个环上)。 初始状态下，假设已知某个起点节点为节点S。现设两个指针t和h，将它们均指向S。接着，同时让t和h往前推进，但是二者的速度不同：t每前进1步，h前进2步。只要二者都可以前进而且没有相遇，就如此保持二者的推进。当h无法前进，即到达某个没有后继的节点时，就可以确定从S出发不会遇到环。反之当t与h再次相遇时，就可以确定从S出发一定会进入某个环，设其为环C。如果确定了存在某个环，就可以求此环的起点与长度。

求解环路的长度

上述算法刚判断出存在环C时，显然t和h位于同一节点，设其为节点M。显然，仅需令h不动，而t不断推进，最终又会返回节点M，统计这一次t推进的步数，显然这就是环C的长度。

求解环路的起点

为了求出环C的起点，只要令h仍均位于节点M，而令t移动至起点节点S，此时h与t之间距为环C长度的整数倍。随后，同时让t和h往前推进，且保持二者的速度相同：t每前进1步，h前进1步。持续该过程直至t与h再一次相遇，设此次相遇时位于同一节点P，则节点P即为从节点S出发所到达的环C的第一个节点，即环C的一个起点。

对于环路起点算法的解释：

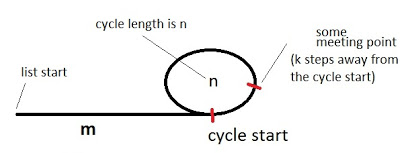
假设出发起点到环起点的距离为m，已经确定有环，环的周长为n，（第一次）相遇点距离环的起点的距离是k。那么当两者相遇时，慢指针（t）移动的总距离i = m + a * n + k，快指针（h）的移动距离为2i，2i = m + b * n + k。其中，a和b分别为t和h在第一次相遇时转过的圈数。让两者相减（快减慢），那么有i = (b - a) * n。即i是圈长度的倍数，b*n和a*n都是环长度的倍数。

​ i=(b-a)*n = m+a*n+k ==> 3i = b*n+i+m+k = m+k+i ==> 2i = m+k，所以得出m+k是环长的整数倍

将一个指针移到出发起点S，另一个指针仍呆在相遇节点M处，两者同时移动，每次移动一步。当第一个指针前进了m，即到达环起点时，另一个指针距离链表起点为m+k 。考虑到m+k为圈长度的倍数，可以理解为指针从链表起点出发，走到环起点，然后绕环转了几圈，所以第二个指针也必然在环的起点。即两者相遇点就是环的起点。

伪代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

t := &S
h := &S                                        //令指针t和h均指向起点节点S。
repeat
    t := t->next
    h := h->next
    if h is not NULL                                //要注意这一判断一般不能省略
            h := h->next
until t = h or h = NULL
if h != NULL                                       //如果存在环的话
    n := 0
    repeat                                              //求环的长度
            t := t->next
            n := n+1
    until t = h
    t := &S                                     //求环的一个起点
    while t != h
            t := t->next
            h := h->next
    P := *t

算法复杂度

• **时间复杂度：**注意到当指针t到达环C的一个起点节点P时(此时指针h显然在环C上)，之后指针t最多仅可能走1圈。若设节点S到P距离为 m，环C的长度为 n，则时间复杂度为 O(m+n)，是线性时间的算法。

• **空间复杂度：**仅需要创立指针t、指针h，保存环长n、环的一个起点P。空间复杂度为 O(1)，是常数空间的算法

KMP算法

博客参考 => 很详尽的KMP算法&详解KMP中next数组求解

暴力匹配算法

假设现在我们面7899临这样一个问题：有一个0410文本串S，和一个模式串P，现在要查找P在S中的位置，怎么查找呢？

如果用暴力匹配的思路，并假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置，则有：

• 如果当前字符匹配成功（即S[i] == P[j]），则i++，j++，继续匹配下一个字符；
• 如果失配（即S[i]! = P[j]），令i = i - (j - 1)，j = 0。相当于每次匹配失败时，i回溯到下一个字符，j被置为0。

暴力匹配算法咋一看好像也没啥，能解决问题。但是如果需要匹配的字符串重复字符太多的话会发生什么呢？

例如，文本串txt=BBC ABCDAB ABCDABCDABDE，子串p=ABCDABD。

KMP算法

在上面那个例子里，如果采用暴力匹配时，每次子串p匹配失败时，都会使得文本串txt回溯到下一个字符，显然这样回溯时间复杂度很高，而且可以发现其实我们没必要回溯到下一个字符，也就是要减少匹配的趟数。

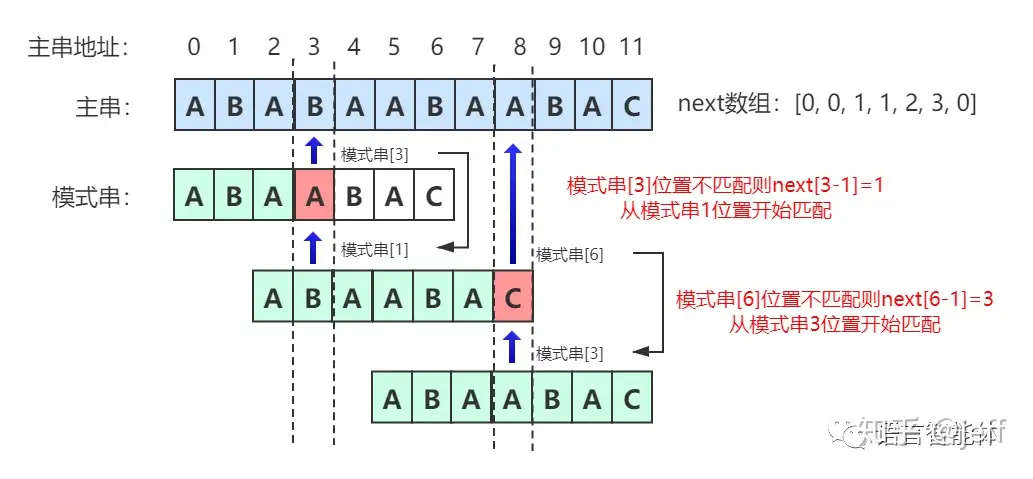
那么，如何减少匹配的趟数呢？其实在每一次匹配过程中，我们就能够判断后续几次匹配是否会成功，算法的核心就是每次匹配过程中推断出后续完全不可能匹配成功的匹配过程，从而减少比较的趟数，如图所示：

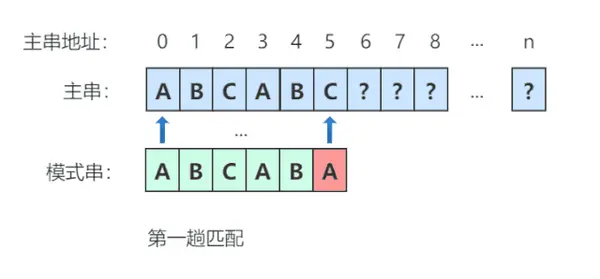
因此，第一次匹配过之后，就可以得出可以直接跳到第四趟再进行判断的结论了。因为第一次匹配的时候，前5个序列和主串相同，只需要对模式串进行分析，模式串出现了重复单元(即AB)，在第一次匹配失败后就可以直接跳跃到出现重复单元的位置。

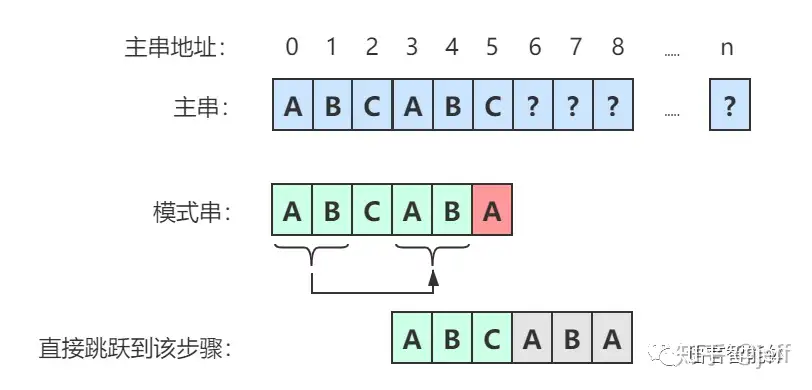
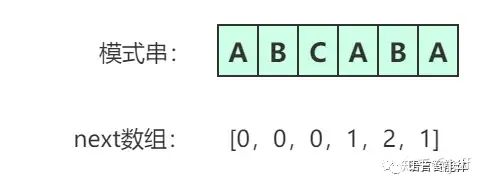
next数组

next数组实质上就是找出模式串中前后字符重复出现的个数，为了能够跳跃不可能匹配的步骤。 next数组的定义为：next[i]表示模式串A[0]至A[i]这个字串，使得前k个字符等于后k个字符的最大值，特别的k不能取i+i,因为字串一共才i+1个字符，自己跟自己相等毫无意义。

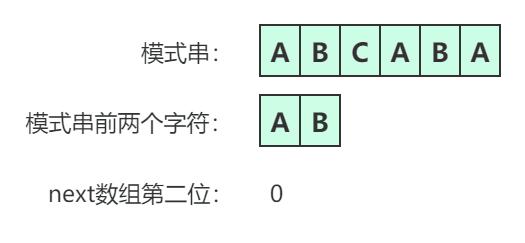
最终得到next数组为：

如何确定在移动过程中需要跳过多少步呢？下图更直观的体现了跳跃的过程：

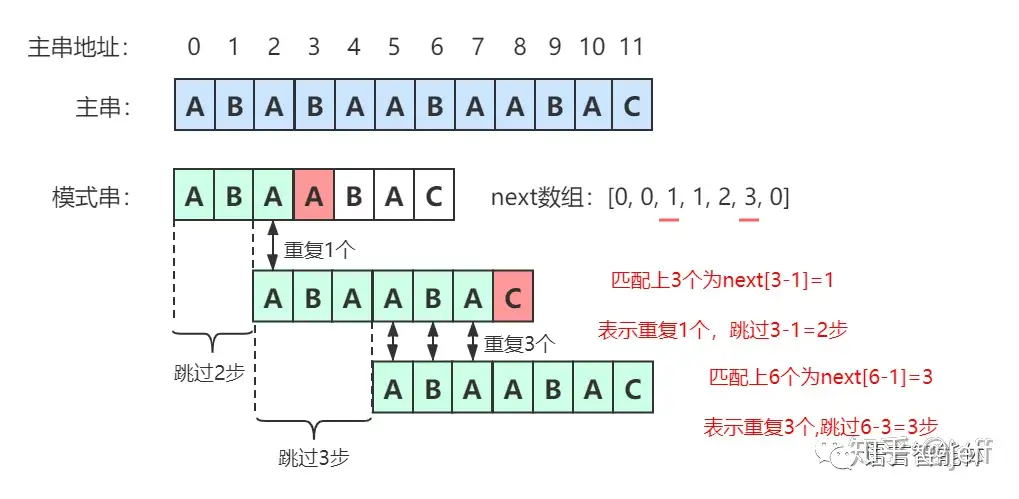
对于上述红色部分的计算跳过长度的公式为跳过的趟数=匹配上字符串中间字符长度-重复字符串长度

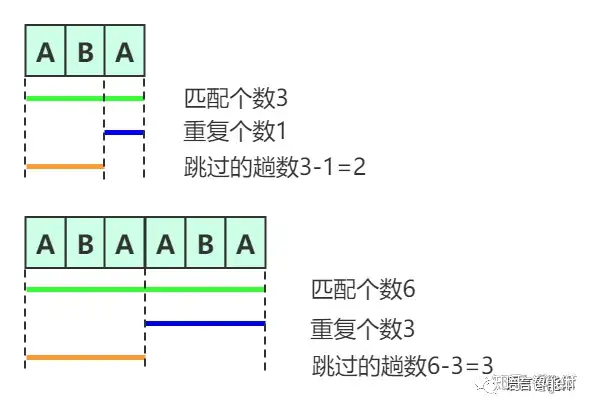
跳过这些步骤后并非再从头开始匹配，而是从重复位置开始匹配：

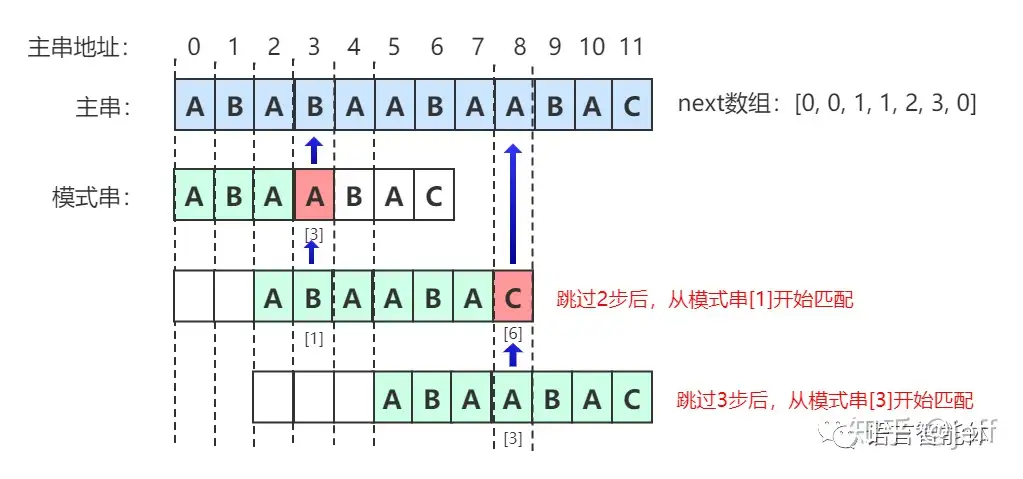
最终，我们不难得出如下结论：

快速幂算法

递归思想

「快速幂算法」的本质是分治算法。举个例子，如果我们要计算 x^64^，我们可以按照： $$ x \to x^2 \to x^4 \to x^8 \to x^{16} \to x^{32} \to x^{64} $$ 的顺序，从 x 开始，每次直接把上一次的结果进行平方，计算 66 次就可以得到 x^64^ 的值，而不需要对 x 乘 63 次 x。

再举一个例子，如果我们要计算 x^77^，我们可以按照： $$ x \to x^2 \to x^4 \to x^9 \to x^{19} \to x^{38} \to x^{77} $$ 的顺序，在 $$x \to x^2，x^2 \to x^4，x^{19} \to x^{38}$$ 这些步骤中，我们直接把上一次的结果进行平方，而在 $$x^4 \to x^9，x^9 \to x^{19}，x^{38} \to x^{77}$$ 这些步骤中，我们把上一次的结果进行平方后，还要额外乘一个 x。

直接从左到右进行推导看上去很困难，因为在每一步中，我们不知道在将上一次的结果平方之后，还需不需要额外乘 x。但如果我们从右往左看，分治的思想就十分明显了：

• 当我们要计算 x^n^ 时，我们可以先递归地计算出 $$y = x^{\lfloor n/2 \rfloor}$$，其中 $$\lfloor a \rfloor$$ 表示对 a 进行下取整；
• 根据递归计算的结果，如果 n 为偶数，那么 x^n^ = y^2^；如果 n 为奇数，那么 x^n^ = y^2^ ；
• 递归的边界为 n = 0，任意数的 0 次方均为 1。

由于每次递归都会使得指数减少一半，因此递归的层数为 O(log n)，算法可以在很快的时间内得到结果。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

class Solution {
    public double myPow(double x, int n) {
        long N = n;
        return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
    }

    public double quickMul(double x, long N) {
        if (N == 0) {
            return 1.0;
        }
        double y = quickMul(x, N / 2);
        return N % 2 == 0 ? y * y : y * y * x;
    }
}

复杂度分析

• 时间复杂度：O(log n)，即为递归的层数。
• 空间复杂度：O(log n)，即为递归的层数。这是由于递归的函数调用会使用栈空间。

迭代思想

由于递归需要使用额外的栈空间，我们试着将递归转写为迭代。在方法一中，我们也提到过，从左到右进行推导是不容易的，因为我们不知道是否需要额外乘 x。但我们不妨找一找规律，看看哪些地方额外乘了 x，并且它们对答案产生了什么影响。

我们还是以 x^77^ 作为例子： $$ x \to x^2 \to x^4 \to^+ x^9 \to^+ x^{19} \to x^{38} \to^+ x^{77} $$ 并且把需要额外乘 x 的步骤打上了 + 标记。可以发现：

• $$x^{38} \to^+ x^{77}$$ 中额外乘的 x 在 x^77^ 中贡献了 x；
• $$x^9 \to^+ x^{19}$$ 中额外乘的 x 在之后被平方了 2 次，因此在 x^77^ 中贡献了 $$x^{2^2} = x^4$$；
• $$x^4 \to^+ x^9$$ 中额外乘的 x 在之后被平方了 3 次，因此在 x^77^ 中贡献了 $$x^{2^3} = x^8$$；
• 最初的 x 在之后被平方了 6 次，因此在 x^77^ 中贡献了 $$x^{2^6} = x^{64}$$。

我们把这些贡献相乘，$$x \times x^4 \times x^8 \times x^{64}$$ 恰好等于 x^77^。而这些贡献的指数部分又是什么呢？它们都是 2 的幂次，这是因为每个额外乘的 x 在之后都会被平方若干次。而这些指数 1，4，8 和 64，**恰好就对应了 77 的二进制表示 (1001101)~2~ 中的每个 1！

因此我们借助整数的二进制拆分，就可以得到迭代计算的方法，一般地，如果整数 n 的二进制拆分为 $$ n = 2^{i_0} + 2^{i_1} + \cdots + 2^{i_k} $$ 那么 $$ x^n = x^{2^{i_0}} \times x^{2^{i_1}} \times \cdots \times x^{2^{i_k}} $$ 这样以来，我们从 x 开始不断地进行平方，得到 $$x^2, x^4, x^8, x^{16}, \cdots$$，如果 n 的第 k 个（从右往左，从 0 开始计数）二进制位为 1，那么我们就将对应的贡献 $$x^{2^k}$$计入答案。

下面的代码给出了详细的注释。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
    public double myPow(double x, int n) {
        long N = n;
        return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
    }

    public double quickMul(double x, long N) {
        double ans = 1.0;
        // 贡献的初始值为 x
        double x_contribute = x;
        // 在对 N 进行二进制拆分的同时计算答案
        while (N > 0) {
            if (N % 2 == 1) {
                // 如果 N 二进制表示的最低位为 1，那么需要计入贡献
                ans *= x_contribute;
            }
            // 将贡献不断地平方
            x_contribute *= x_contribute;
            // 舍弃 N 二进制表示的最低位，这样我们每次只要判断最低位即可
            N /= 2;
        }
        return ans;
    }
}

贪心算法

转载 => https://mp.weixin.qq.com/s?__biz=MzI0NjAxMDU5NA==&mid=2475930307&idx=1&sn=243c7b43b5aa3919129d0ac40a1b2fab&chksm=ff22d54ec8555c586a07dbcfe671bdf6d79278ebcf42c706008211f54361a4556149ad911681&token=1439040973&lang=zh_CN#rd

大家好呀，我是帅蛋。

今天我们来学习贪心算法，它和我之前带大家玩儿的【递归算法】、【分治算法】类似，带着算法的名儿，但实际上是一种解决问题的思想策略。

在正式开始之前，我想先说几句题外话：

我知道贪心算法对很多同学来说有点难，这个难不是难在对概念的理解上，而是一看就会，一做题就废，接着半途而废。

这个我想说很正常，因为贪心算法是一种算法【思想】，但凡是这种的，就没什么套路可讲，不像我们在上个专题学二叉树的时候，解题就是递归 + 迭代，可以由上到下、由下到上、由左到右的整，套路明显。

更不用说，后面碰到动态规划的时候，更容易贪心算法和动态规划用哪个傻傻分不清楚。

碰到这些问题怎么办？就是干，唯做题 + 总结。

写这篇文章应该篇幅不会很多，我会带你了解一下什么是贪心算法，重头戏是会在后面的实战题板块，我来带你做题和做总结，所以跟着搞就完事了。

R u ready？gogogo！

贪心算法

学习贪心算法，首先我们得从它的概念学起。

贪心算法（greedy algorithm）是指从问题初始转状态出发，通过在每一步选择中都采取最好或者最优（最有利）的选择，从而得到结果的最优值（或较优值）。

通过概念我们能知道贪心算法的 2 个关键点：

• 贪心算法在对问题进行求解时，总是做出当前看来最好的选择。
• 通过贪心算法所得到的结果不一定是最优的结果，但肯定都是相对接近最优解的结果。

看起来这 2 点可能不好理解，我用两个例子你就懂了。

例 1：我们现在有 20、10、5、1 这 4 种数额的钱币，如果想要凑齐 36 元，那我最少需要几张钱币？

如果根据贪心算法的话，我们上来肯定是看需要几张 20 的，这道题需要 1 张，那还剩 36 - 20 = 16。

看完 20 的我们再来看 10 元的，需要 1 张 10 元，现在还剩 16 - 10 = 6。

下面继续是看 5 和 1，分别就需要 1 张。

最后我们得到的答案是，如果想要凑齐 36 元我们最少需要 4 张纸币。

这个例子，每次都是用最大的纸币去匹配，剩下的余额再用较小点的面额去匹配，这个就是第 1 点我们说的，在对问题进行求解时，每次都是做出当前看来最好的选择。

例 2：我们还是以撒币为例，现在我们有 10、9、1 这 3 种金额的钱币，如果想要凑齐 18 元，咱最少需要几张钱币？

在这个例子，如果我们还是用上面的贪心策略，那就完蛋了。

我上来就看需要几张 10 元，那这道题需要 1 张，剩余金额是 8 元，那我无法用 9 的纸币，只能用 8 张 1 元的纸币，那这最后的结果是用了 9 张纸币。

而通过小学知识，我们肉眼就能看出用 2 张 9 元的纸币就 ok 了。

通过这个例子就是说明了第 2 点：通过贪心算法所得到的结果不一定是最优的结过。

看到这是不是懵了？懵了就对了。

你现在就先记住一点：贪心算法只是在部分情况下有用。至于什么是部分情况，这个就得靠多做题了~

诶诶诶，你先别动手，那你看嘛，就比如上面的 2 个例子，你要看看数之间的规律，例 1 的中的币互相成倍数，例 2 中就没啥规律。

这个就得是靠多做题多总结好伐~

什么时候用贪心？

说实话，这就是贪心算法对我们来说”难“的地方，即没有模式化的东西直接了当的告诉我们”这样就是用贪心“。

如果硬要说的话，绝大多数用在像上一节中举的例子那种【组合优化】问题，求解的过程涉及到多步判断。

碰到这样的题，你的想法可以往贪心算法上靠一靠，但也只是”可以“而已。

因为你看到类似这种问题，你想到贪心算法，首先就要自己先搞出个贪心策略，之后你要验证你所用的贪心策略产生的结果是不是最优的，如果不是最优的，那可能就要用到我们下一个专题要学的【动态规划】。

大家估计会问如何验证，直接就举几个靠谱的例子验证就好了。

当然这里我说的是”靠谱“，就是一些特例，不然你随便整了几个例子，发现都对，这个时候你就觉得你做的就是对的，恰恰也可能你举的这几个例子正好巧了。

这里我还想多说几句：

其实按照正常来说呢，像这种验证贪心算法的正确性，最靠谱的就是通过数学推导来弄，一般像什么数学归纳法、反正法这种方法。

但是怎么说呢，数学推导虽然很对，结果也很正确，但是对于我们来说完全没有必要，且不说很多人根本不会推导，就算会，对我们来说意义也不大，毕竟目的性不一样，这样搞就走远了。

从我们刷题的角度来看，我们完全就可以靠举一些特例就能验证绝大多数问题。

当然像这种举特例的能力，你要问我怎么举，我只能告诉你：多做题就有了。

贪心法解题步骤

贪心算法的解题步骤，其实和分治算法很像的。

我在之前讲分治算法的时候讲过分治算法的 3 个步骤：

划分（Divide）：将原问题划分为规模较小的子问题，子问题相互独立，与原问题形式相同。

求解（Conquer）：递归的求解划分之后的子问题。

合并（Combine）：这一步非必须。有些问题涉及合并子问题的解，将子问题的解合并成原问题的解。有的问题则不需要，只是求出子问题的解即可。

贪心算法的步骤也类似，如果你确定是贪心算法可解，也是 3 个步骤：

(1) 将问题分解为多个子问题。

(2) 选择合适的贪心策略，得到每一个子问题的局部最优解。

(3) 将子问题的局部最优解合并成原问题的最优解。

是不是这么看觉得还挺简单的？嘿嘿嘿嘿，等做题的时候你就知道有时候看到的并不就是真实的感受~

贪心算法的内容到这就说的差不多了，单纯理论上的东西确实不多，看完了也只是让你有个印象。

关于理论上的东西你只要了解就行，你想学好贪心别无他法。就是要多做题多练习，见的多了就有感觉了。

其实一连套的动作就是：诶，这道题看着能用贪心，试试，得出个结果，找几个特例验一验，是最优解万事大吉，不是最优解，就再想想是不是动态规划啥的可以解。

最后再说一句，贪心算法不用慌，退一万步讲，贪心就算学的不好，问题也不大，面试的时候贪心考的一般比较少。

毕竟生活啊，总归是要全局考虑，哪能只盯着眼前~

我是帅蛋，我们下次见！

动态规划算法

转载 => https://mp.weixin.qq.com/s?__biz=MzI0NjAxMDU5NA==&mid=2475932264&idx=1&sn=465412392bab644f2391c62148fcac2c&chksm=ff22dde5c85554f3b66668a590b63c6ed27859ca83cf4018ede7653d25adf24764574adde5fc&token=239743856&lang=zh_CN#rd

大家好呀，我是帅蛋！

很多同学在动态规划和贪心算法上有些傻傻分不清楚，今天我就来解决动态规划和贪心算法的比较分析，当作加餐。

前面我先比较概念，后面我会用两个例子带大家一步步分析。

我尽量以我的理解给大家讲清楚！

动态规划 vs 贪心算法

我在【动态规划】的文章中写过：

动态规划将一个大的复杂的问题，拆成一个个的子问题，子问题再拆成更小的子问题，直至拆到到子问题可以用确定的条件解答，之后通过这些子问题的解反向得到原问题的解。

它可以解决的问题包含 4 个特点：

• 求最优性质问题
• 有重叠子问题
• 最优子结构
• 无后效性

同样，我在【贪心算法】的文章中也解释过贪心的概念：

**贪心算法（greedy algorithm）**是指从问题初始转状态出发，通过在每一步选择中都采取最好或者最优（最有利）的选择，从而得到结果的最优值（或较优值）。

通过概念我们能知道贪心算法的 2 个关键点：

• 贪心算法在对问题进行求解时，总是做出当前看来最好的选择。
• 通过贪心算法所得到的结果不一定是最优的结果，但肯定都是相对接近最优解的结果。

从贪心的概念提炼一下，其实贪心能解决的问题也包含 4 个特点：

• 求最优性质问题
• 贪心选择
• 最优子结构
• 无后效性：无后向性是指 以前出现状态 和 以前状态的变化过程 不会影响 将来的变化。

综合可以看出，贪心和动态规划：

相似之处在于，都是求最优性质问题，问题具有”无后效性“，解决办法都是将问题拆成子问题，都有“最优子结构”。

但区别是，贪心算法独有的”贪心选择“，它选的是当前最优解，而动态规划是通过子问题的最优解推出当前的最优解。

又是说了一堆概念上的东西，可能你看了还是觉得有点抽象很难解释。

’ fill=’%23FFFFFF’%3E%3Crect x=‘249’ y=‘126’ width=‘1’ height=‘1’%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)

诶诶诶，别动手，下面讲具体的了！我就用两个例子来解释一下~

’ fill=’%23FFFFFF’%3E%3Crect x=‘249’ y=‘126’ width=‘1’ height=‘1’%3E%3C/rect%3E%3C/g%3E%3C/g%3E%3C/svg%3E)

**问题：**我们现在有 20、10、5、1 这 4 种数额的钱币，如果想要凑齐 36 元，那我最少需要几张钱币？

如果根据贪心算法的话，我们上来肯定是看需要几张 20 的，这道题需要 1 张，那还剩 36 - 20 = 16。

看完 20 的我们再来看 10 元的，需要 1 张 10 元，现在还剩 16 - 10 = 6。

下面继续是看 5 和 1，分别就需要 1 张。

最后我们得到的答案是，如果想要凑齐 36 元我们最少需要 4 张纸币。

这个例子，每次都是用最大的纸币去匹配，剩下的余额再用较小点的面额去匹配，这个就是贪心算法中我们说的，在对问题进行求解时，每次都是做出当前看来最好的选择。

上面这个问题你看贪心可以，还挺得瑟，那你看我换一下。

**问题：**还是以撒币为例，现在我们有 10、9、1 这 3 种金额的钱币，如果想要凑齐 18 元，咱最少需要几张钱币？

如果用贪心的话，我上来就看需要几张 10 元，那这道题需要 1 张，剩余金额是 8 元，那我无法用 9 的纸币，只能用 8 张 1 元的纸币，那这最后的结果是用了 9 张纸币。

但是明明我们一眼就能看出用 2 张 9 元的纸币就 ok 了。

这就是贪心算法”贪心选择“局限的地方，只考虑眼前的情况。

我们重新分析这个例子。

想要凑齐 18 元，如果我们取的金额钱币为 10，下面我们就要凑齐 18 - 10 = 8 元；如果取得金额钱币为 9，下面我们就要凑齐 18 - 9 = 9 元。

这些问题其实都有一个相同的形式：为了凑齐 xx 元，最少需要几张钱币。这里我用 dp[n] 表示“凑出 n 元需要的最少钱币数”。

对于凑齐 18 元，如果我们选了 10 元金额，那：

dp[18] = dp[8] + 1 = 8 + 1 = 9。

意思是利用 10 元凑出 18，相当于是“凑齐 8 元需要的纸币数 + 这一张 10 元钱币”。至于 dp[8] 怎么求出来的我们先不管。

同理：

选 9 元钱币，dp[18] = dp[9] + 1 = 1 + 1 = 2。

选 1 元钱币，dp[18] = dp[17] + 1 = 8 + 1 = 9。

显而易见的是，凑出 18 需要的最小钱币数是 2，是选取 9 这张钱币的方案。

我们通过上面三个公式做出了正确的决策。

可以看出 dp[18] 是与 dp[18 - 10]、dp[18 - 9]、dp[18 - 1] 有关，放大来看，即 dp[n] 与 dp[n - 10]、dp[n - 9]、dp[n - 1] 有关：

dp[n] = min(dp[n - 10], dp[n - 9], dp[n - 1]) + 1。

你看，我们想要求出 dp[n]，只需要管 dp[n - 10]、dp[n - 9]、dp[n - 1] ，至于更小的值是怎么求的，和我 dp[n] 就没关系了。

这也是动态规划的“无后效性”的完美解释。

动态规划保证了我们解决问题的结果的正确性，比起贪心只关心眼前，动态规划会分别算出每种情况的最优解，从而得出自己的最优解。

现在你再看这句话：

贪心算法选的是当前最优解，而动态规划****是通过子问题的最优解推出当前的最优解。

是不是就突然理解了呢，这就是最关键的地方，下次再有人问你，别和他扯别的，就说这句话！

背包问题

原文地址： https://zhuanlan.zhihu.com/p/93857890

背包问题是一类经典的动态规划问题，它非常灵活，需要仔细琢磨体会，本文先对背包问题的几种常见类型作一个总结，然后再看看LeetCode上几个相关题目。

本文首发于我的博客，传送门

根据维基百科，背包问题（Knapsack problem）是一种组合优化的NP完全（NP-Complete，NPC）问题。问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。NPC问题是没有多项式时间复杂度的解法的，但是利用动态规划，我们可以以伪多项式时间复杂度求解背包问题。一般来讲，背包问题有以下几种分类：

1. 01背包问题
2. 完全背包问题
3. 多重背包问题

此外，还存在一些其他考法，例如恰好装满、求方案总数、求所有的方案等。本文接下来就分别讨论一下这些问题。

1. 01背包

1.1 题目

最基本的背包问题就是01背包问题（01 knapsack problem）：一共有N件物品，第i（i从1开始）件物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够装入背包的最大价值是多少？

1.2 分析

如果采用暴力穷举的方式，每件物品都存在装入和不装入两种情况，所以总的时间复杂度是O(2^N)，这是不可接受的。而使用动态规划可以将复杂度降至O(NW)。我们的目标是书包内物品的总价值，而变量是物品和书包的限重，所以我们可定义状态dp:

1

dp[i][j]表示将前i件物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W

那么我们可以将dp[0][0…W]初始化为0，表示将前0个物品（即没有物品）装入书包的最大价值为0。那么当 i > 0 时dp[i][j]有两种情况：

1. 不装入第i件物品，即dp[i−1][j]；
2. 装入第i件物品（前提是能装下），即dp[i−1][j−w[i]] + v[i]。

即状态转移方程为

1

dp[i][j] = max(dp[i−1][j], dp[i−1][j−w[i]]+v[i]) // j >= w[i]

由上述状态转移方程可知，dp[i][j]的值只与dp[i-1][0,...,j-1]有关，所以我们可以采用动态规划常用的方法（滚动数组）对空间进行优化（即去掉dp的第一维）。需要注意的是，为了防止上一层循环的dp[0,...,j-1]被覆盖，循环的时候 j 只能逆向枚举（空间优化前没有这个限制），伪代码为：

1
2
3
4
5

// 01背包问题伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
    for j = W,...,w[i] // 必须逆向枚举!!!
        dp[j] = max(dp[j], dp[j−w[i]]+v[i])

时间复杂度为O(NW), 空间复杂度为O(W)。由于W的值是W的位数的幂，所以这个时间复杂度是伪多项式时间。

动态规划的核心思想避免重复计算在01背包问题中体现得淋漓尽致。第i件物品装入或者不装入而获得的最大价值完全可以由前面i-1件物品的最大价值决定，暴力枚举忽略了这个事实。

2. 完全背包

2.1 题目

完全背包（unbounded knapsack problem）与01背包不同就是每种物品可以有无限多个：一共有N种物品，每种物品有无限多个，第i（i从1开始）种物品的重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够装入背包的最大价值是多少？

2.2 分析一

我们的目标和变量和01背包没有区别，所以我们可定义与01背包问题几乎完全相同的状态dp:

1

dp[i][j]表示将前i种物品装进限重为j的背包可以获得的最大价值, 0<=i<=N, 0<=j<=W

初始状态也是一样的，我们将dp[0][0…W]初始化为0，表示将前0种物品（即没有物品）装入书包的最大价值为0。那么当 i > 0 时dp[i][j]也有两种情况：

1. 不装入第i种物品，即dp[i−1][j]，同01背包；
2. 装入第i种物品，此时和01背包不太一样，因为每种物品有无限个（但注意书包限重是有限的），所以此时不应该转移到dp[i−1][j−w[i]]而应该转移到dp[i][j−w[i]]，即装入第i种商品后还可以再继续装入第种商品。

所以状态转移方程为

1

dp[i][j] = max(dp[i−1][j], dp[i][j−w[i]]+v[i]) // j >= w[i]

这个状态转移方程与01背包问题唯一不同就是max第二项不是dp[i-1]而是dp[i]。

和01背包问题类似，也可进行空间优化，优化后不同点在于这里的 j 只能正向枚举而01背包只能逆向枚举，因为这里的max第二项是dp[i]而01背包是dp[i-1]，即这里就是需要覆盖而01背包需要避免覆盖。所以伪代码如下：

1
2
3
4
5

// 完全背包问题思路一伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
    for j = w[i],...,W // 必须正向枚举!!!
        dp[j] = max(dp[j], dp[j−w[i]]+v[i])

由上述伪代码看出，01背包和完全背包问题此解法的空间优化版解法唯一不同就是前者的 j 只能逆向枚举而后者的 j 只能正向枚举，这是由二者的状态转移方程决定的。此解法时间复杂度为O(NW), 空间复杂度为O(W)。

2.3 分析二

除了分析一的思路外，完全背包还有一种常见的思路，但是复杂度高一些。我们从装入第 i 种物品多少件出发，01背包只有两种情况即取0件和取1件，而这里是取0件、1件、2件…直到超过限重（k > j/w[i]），所以状态转移方程为：

1
2

# k为装入第i种物品的件数, k <= j/w[i]
dp[i][j] = max{(dp[i-1][j − k*w[i]] + k*v[i]) for every k}

同理也可以进行空间优化，需要注意的是，这里max里面是dp[i-1]，和01背包一样，所以 j 必须逆向枚举，优化后伪代码为

1
2
3
4
5
6

// 完全背包问题思路二伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
    for j = W,...,w[i] // 必须逆向枚举!!!
        for k = [0, 1,..., j/w[i]]
            dp[j] = max(dp[j], dp[j−k*w[i]]+k*v[i])

相比于分析一，此种方法不是在O(1)时间求得dp[i][j]，所以总的时间复杂度就比分析一大些了，为 �(����¯)级别。

2.4 分析三、转换成01背包

01背包问题是最基本的背包问题，我们可以考虑把完全背包问题转化为01背包问题来解：将一种物品转换成若干件只能装入0件或者1件的01背包中的物品。

最简单的想法是，考虑到第 i 种物品最多装入 W/w[i] 件，于是可以把第 i 种物品转化为 W/w[i] 件费用及价值均不变的物品，然后求解这个01背包问题。

更高效的转化方法是采用二进制的思想：把第 i 种物品拆成重量为 ��2� 、价值为 ��2� 的若干件物品，其中 k 取遍满足 ��2�≤� 的非负整数。这是因为不管最优策略选几件第 i 种物品，总可以表示成若干个刚才这些物品的和（例：13 = 1 + 4 + 8）。这样就将转换后的物品数目降成了对数级别。

3. 多重背包

3.1 题目

多重背包（bounded knapsack problem）与前面不同就是每种物品是有限个：一共有N种物品，第i（i从1开始）种物品的数量为n[i]，重量为w[i]，价值为v[i]。在总重量不超过背包承载上限W的情况下，能够装入背包的最大价值是多少？

3.2 分析一

此时的分析和完全背包的分析二差不多，也是从装入第 i 种物品多少件出发：装入第i种物品0件、1件、…n[i]件（还要满足不超过限重）。所以状态方程为：

1
2

# k为装入第i种物品的件数, k <= min(n[i], j/w[i])
dp[i][j] = max{(dp[i-1][j − k*w[i]] + k*v[i]) for every k}

同理也可以进行空间优化，而且 j 也必须逆向枚举，优化后伪代码为

1
2
3
4
5
6

// 完全背包问题思路二伪代码(空间优化版)
dp[0,...,W] = 0
for i = 1,...,N
    for j = W,...,w[i] // 必须逆向枚举!!!
        for k = [0, 1,..., min(n[i], j/w[i])]
            dp[j] = max(dp[j], dp[j−k*w[i]]+k*v[i])

3.3 分析二、转换成01背包

采用2.4节类似的思路可以将多重背包转换成01背包问题，采用二进制思路将第 i 种物品分成了 �(�����) 件物品，将原问题转化为了复杂度为 �(�∑������) 的 01 背包问题，相对于分析一是很大的改进。

4. 其他情形

除了上述三种基本的背包问题外，还有一些其他的变种，如下图所示（图片来源）。

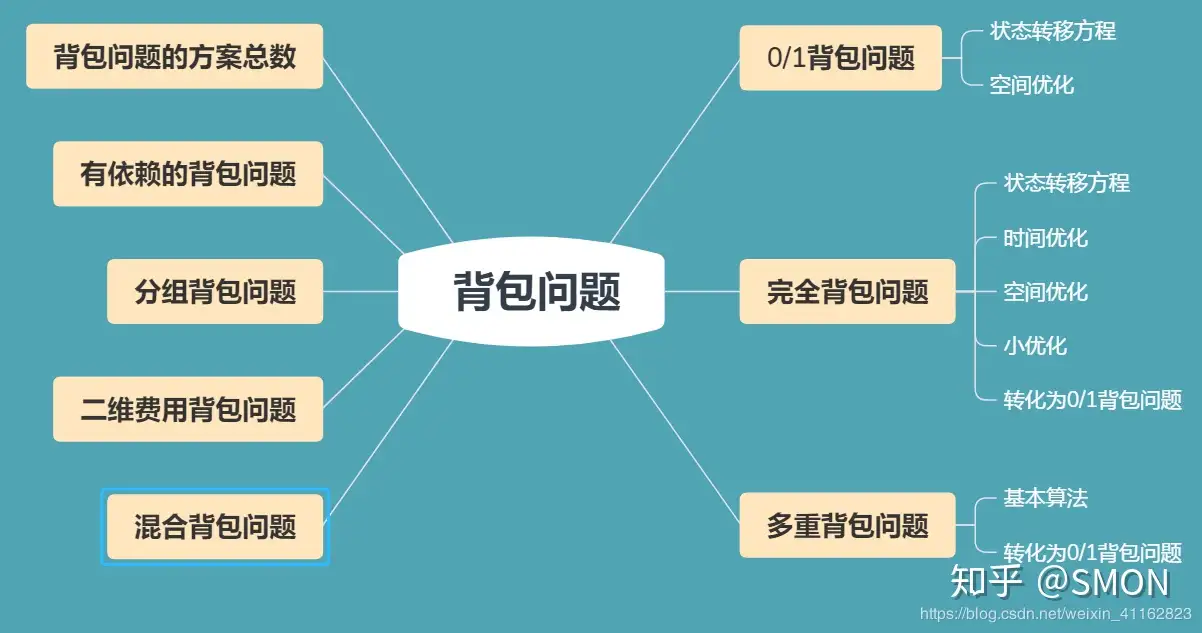
本节列举几种比较常见的。

4.1 恰好装满

背包问题有时候还有一个限制就是必须恰好装满背包，此时基本思路没有区别，只是在初始化的时候有所不同。

如果没有恰好装满背包的限制，我们将dp全部初始化成0就可以了。因为任何容量的背包都有一个合法解“什么都不装”，这个解的价值为0，所以初始时状态的值也就全部为0了。如果有恰好装满的限制，那只应该将dp[0,…,N][0]初始为0，其它dp值均初始化为-inf，因为此时只有容量为0的背包可以在什么也不装情况下被“恰好装满”，其它容量的背包初始均没有合法的解，应该被初始化为-inf。

4.2 求方案总数

除了在给定每个物品的价值后求可得到的最大价值外，还有一类问题是问装满背包或将背包装至某一指定容量的方案总数。对于这类问题，需要将状态转移方程中的 max 改成 sum ，大体思路是不变的。例如若每件物品均是完全背包中的物品，转移方程即为

1

dp[i][j] = sum(dp[i−1][j], dp[i][j−w[i]]) // j >= w[i]

4.3 二维背包

前面讨论的背包容量都是一个量：重量。二维背包问题是指每个背包有两个限制条件（比如重量和体积限制），选择物品必须要满足这两个条件。此类问题的解法和一维背包问题不同就是dp数组要多开一维，其他和一维背包完全一样，例如5.4节。

4.4 求最优方案

一般而言，背包问题是要求一个最优值，如果要求输出这个最优值的方案，可以参照一般动态规划问题输出方案的方法：记录下每个状态的最优值是由哪一个策略推出来的，这样便可根据这条策略找到上一个状态，从上一个状态接着向前推即可。

以01背包为例，我们可以再用一个数组G[i][j]来记录方案，设 G[i][j] = 0表示计算 dp[i][j] 的值时是采用了max中的前一项(也即dp[i−1][j])，G[i][j] = 1 表示采用了方程的后一项。即分别表示了两种策略: 未装入第 i 个物品及装了第 i 个物品。其实我们也可以直接从求好的dp[i][j]反推方案：若 dp[i][j] = dp[i−1][j] 说明未选第i个物品，反之说明选了。

5. LeetCode相关题目

本节对LeetCode上面的背包问题进行讨论。

5.1 Partition Equal Subset Sum（分割等和子集）

Loading…leetcode.com/problems/partition-equal-subset-sum/

题目给定一个只包含正整数的非空数组。问是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

由于所有元素的和sum已知，所以两个子集的和都应该是sum/2（所以前提是sum不能是奇数），即题目转换成从这个数组里面选取一些元素使这些元素和为sum/2。如果我们将所有元素的值看做是物品的重量，每件物品价值都为1，所以这就是一个恰好装满的01背包问题。

我们定义空间优化后的状态数组dp，由于是恰好装满，所以应该将dp[0]初始化为0而将其他全部初始化为INT_MIN，然后按照类似1.2节的伪代码更新dp：

1
2
3
4
5
6

int capacity = sum / 2;
vector<int>dp(capacity + 1, INT_MIN);
dp[0] = 0;
for(int i = 1; i <= n; i++)
    for(int j = capacity; j >= nums[i-1]; j--)
        dp[j] = max(dp[j], 1 + dp[j - nums[i-1]]);

更新完毕后，如果dp[sum/2]大于0说明满足题意。

由于此题最后求的是能不能进行划分，所以dp的每个元素定义成bool型就可以了，然后将dp[0]初始为true其他初始化为false，而转移方程就应该是用或操作而不是max操作。完整代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

bool canPartition(vector<int>& nums) {
    int sum = 0, n = nums.size();
    for(int &num: nums) sum += num;
    if(sum % 2) return false;

    int capacity = sum / 2;
    vector<bool>dp(capacity + 1, false);
    dp[0] = true;
    for(int i = 1; i <= n; i++)
        for(int j = capacity; j >= nums[i-1]; j--)
            dp[j] = dp[j] || dp[j - nums[i-1]];

    return dp[capacity];
}

另外此题还有一个更巧妙更快的解法，基本思路是用一个bisets来记录所有可能子集的和，详见我的Github。

5.2 Coin Change（零钱兑换）

Loading…leetcode.com/problems/coin-change/

题目给定一个价值amount和一些面值，假设每个面值的硬币数都是无限的，问我们最少能用几个硬币组成给定的价值。

如果我们将面值看作是物品，面值金额看成是物品的重量，每件物品的价值均为1，这样此题就是是一个恰好装满的完全背包问题了。不过这里不是求最多装入多少物品而是求最少，我们只需要将2.2节的转态转移方程中的max改成min即可，又由于是恰好装满，所以除了dp[0]，其他都应初始化为INT_MAX。完整代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

int coinChange(vector<int>& coins, int amount) {
    vector<int>dp(amount + 1, INT_MAX);
    dp[0] = 0;

    for(int i = 1; i <= coins.size(); i++)
        for(int j = coins[i-1]; j <= amount; j++){
            // 下行代码会在 1+INT_MAX 时溢出
            // dp[j] = min(dp[j], 1 + dp[j - coins[i-1]]); 
            if(dp[j] - 1 > dp[j - coins[i-1]])
                dp[j] = 1 + dp[j - coins[i-1]];   
        }
    return dp[amount] == INT_MAX ? -1 : dp[amount];   
}

注意上面1 + dp[j - coins[i-1]]会存在溢出的风险，所以我们换了个写法。

另外此题还可以进行搜索所有可能然后保持一个全局的结果res，但是直接搜索会超时，所以需要进行精心剪枝，剪枝后可击败99%。详见我的Github。

5.3 Target Sum（目标和）

Loading…leetcode.com/problems/target-sum/

这道题给了我们一个数组（元素非负），和一个目标值，要求给数组中每个数字前添加正号或负号所组成的表达式结果与目标值S相等，求有多少种情况。

假设所有元素和为sum，所有添加正号的元素的和为A，所有添加负号的元素和为B，则有sum = A + B 且 S = A - B，解方程得A = (sum + S)/2。即题目转换成：从数组中选取一些元素使和恰好为(sum + S) / 2。可见这是一个恰好装满的01背包问题，要求所有方案数，将1.2节状态转移方程中的max改成求和即可。需要注意的是，虽然这里是恰好装满，但是dp初始值不应该是inf，因为这里求的不是总价值而是方案数，应该全部初始为0（除了dp[0]初始化为1）。所以代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

int findTargetSumWays(vector<int>& nums, int S) {
    int sum = 0;
    // for(int &num: nums) sum += num;
    sum = accumulate(nums.begin(), nums.end(), 0);
    if(S > sum || sum < -S) return 0; // 肯定不行
    if((S + sum) & 1) return 0; // 奇数
    int target = (S + sum) >> 1;

    vector<int>dp(target + 1, 0);

    dp[0] = 1;
    for(int i = 1; i <= nums.size(); i++)
        for(int j = target; j >= nums[i-1]; j--)
            dp[j] = dp[j] + dp[j - nums[i-1]];

    return dp[target];
}

5.4 Ones and Zeros（一和零）

Loading…leetcode.com/problems/ones-and-zeroes/

题目给定一个仅包含 0 和 1 字符串的数组。任务是从数组中选取尽可能多的字符串，使这些字符串包含的0和1的数目分别不超过m和n。

我们把每个字符串看做是一件物品，把字符串中0的数目和1的数目看做是两种“重量”，所以就变成了一个二维01背包问题，书包的两个限重分别是 m 和 n，要求书包能装下的物品的最大数目（也相当于价值最大，设每个物品价值为1）。

我们可以提前把每个字符串的两个“重量” w0和w1算出来用数组存放，但是注意到只需要用一次这两个值，所以我们只需在用到的时候计算w0和w1就行了，这样就不用额外的数组存放。完整代码如下：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

int findMaxForm(vector<string>& strs, int m, int n) {
    int num = strs.size();
    int w0, w1;

    vector<vector<int>>dp(m+1, vector<int>(n+1, 0));

    for(int i = 1; i <= num; i++){
        w0 = 0; w1 = 0;
        // 计算第i-1个字符串的两个重量
        for(char &c: strs[i - 1]){
            if(c == '0') w0 += 1;
            else w1 += 1;
        }

        // 01背包, 逆向迭代更新dp
        for(int j = m; j >= w0; j--)
            for(int k = n; k >= w1; k--)
                dp[j][k] = max(dp[j][k], 1+dp[j-w0][k-w1]);
    }

    return dp[m][n];
}

6. 总结

本文讨论了几类背包问题及LeetCode相关题目，其中01背包问题和完全背包问题是最常考的，另外还需要注意一些其他变种例如恰好装满、二维背包、求方案总数等等。除了本文讨论的这些背包问题之外，还存在一些其他的变种，但只要深刻领会本文所列的背包问题的思路和状态转移方程，遇到其它的变形问题，应该也不难想出算法。如果想更加详细地理解背包问题，推荐阅读经典的背包问题九讲。