Leetcode刷题笔记

[toc]

day01

移除元素

• 题目

  给你一个数组 nums 和一个值val，你需要 原地 移除所有数值等于val的元素，并返回移除后数组的新长度。

  不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

  元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

  • 暴力题解

    这个题目暴力的解法就是两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

    class Solution { public int removeElement(int[] nums, int val) { int j=0; int i=0; int len=nums.length; for(i=0;i<len;i++){ if(val==nums[i]){ //将之后的元素全部往前挪移覆盖一位 for(j=i+1;j<len;j++){ nums[j-1]=nums[j]; } //将数组索引也往前挪 i--; len--; } } return len; } }

  • 双指针法求解

    由于题目要求删除数组中等于val的元素，因此输出数组的长度一定小于等于输入数组的长度，我们可以把输出的数组直接写在输入数组上。可以使用双指针：右指针right 指向当前将要处理的元素，左指针 left 指向下一个将要赋值的位置。

    如果右指针指向的元素不等于 val，它一定是输出数组的一个元素，我们就将右指针指向的元素复制到左指针位置，然后将左右指针同时右移；

    如果右指针指向的元素等于 val，它不能在输出数组里，此时左指针不动，右指针右移一位。

    整个过程保持不变的性质是：区间 [0,left)中的元素都不等于 val。当左右指针遍历完输入数组以后，left 的值就是输出数组的长度。

    1 2 3 4 5 6 7 8 9 10 11 12 13 14

    class Solution { public int removeElement(int[] nums, int val) { int n = nums.length; int left = 0;//指输出元素索引 for (int right = 0; right < n; right++){ if (nums[right] != val) { //不等于删除值，则将这个元素添加至输出元素 nums[left] = nums[right]; left++; } } return left; } }

day02

最大子数组和

• 题目

  给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。子数组 是数组中的一个连续部分。

• 暴力破解

• 找规律

  对于含有正数的序列而言,最大子序列肯定是正数,所以头尾肯定都是正数.我们可以从第一个正数开始算起,每往后加一个数便更新一次和的最大值;当当前和成为负数时,则表明此前序列无法为后面提供最大子序列和,因此必须重新确定序列首项

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public int maxSubArray(int[] nums) { int maxSum = Integer.MIN_VALUE;//最大和 int thisSum = 0;//当前和 int len = nums.length; for(int i = 0; i < len; i++) { thisSum += nums[i]; if(maxSum < thisSum) { maxSum = thisSum; } //如果当前和小于0则归零，因为对于后面的元素来说这些是减小的。于是归零，意即从此处算开始最大和 if(thisSum < 0) { thisSum = 0; } } return maxSum; } }

加一

• 题目

  给定一个由 整数 组成的 非空 数组所表示的非负整数，在该数的基础上加一。最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。你可以假设除了整数 0 之外，这个整数不会以零开头。

• 找规律

  将这个看作是两个数组相加，辅助数组始终要比给定数组多一位，用来承载可能两数之和比给定数组多一位。两数相加，先从末尾相加，依次往前，满十进一

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  class Solution { public int[] plusOne(int[] digits) { int len1=digits.length; int len2=len1+1; int i,j; int[] arr=new int[len2]; arr[len2-1]=1; for(i=len1-1,j=len2-1;;i--,j--){ int sum=digits[i]+arr[j]; if(sum>9){ //进1 arr[j-1]++; //取余 arr[j]=(sum)%10; }else{ arr[j]=sum; } //跳出条件放到此处，防止少算一次 if (i==0){ break; } } //根据首位判断是否输出首位 if (arr[0]==0){ for (i=1,j=0;i<len2;){ digits[j++]=arr[i++]; } return digits; } return arr; } }

day03

合并两个有序数组

• 题目

  给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

  注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

• 方法一：先合并再排序（缺点，没有利用两数组已经排序的条件）

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public void merge(int[] nums1, int m, int[] nums2, int n) { //先合并末尾数据 for (int i = m, j = 0; i < nums1.length && j < n; i++, j++) { nums1[i] = nums2[j]; } //按递增排序(希尔排序) for (int gap = nums1.length / 2; gap > 0; gap /= 2) {//步长 //对每组进行直接插入排序 for (int i = gap; i < nums1.length; i++) { int index = i; int value = nums1[i]; while (index - gap >= 0 && nums1[index - gap] > value) { nums1[index] = nums1[index - gap]; index -= gap; } nums1[index] = value; } } } }

• 方法二：双指针

  方法一没有利用数组nums1与 nums2已经被排序的性质。为了利用这一性质，我们可以使用双指针方法。这一方法将两个数组看作队列，每次从两个数组头部取出比较小的数字放到结果中。如下面的动画所示：

  

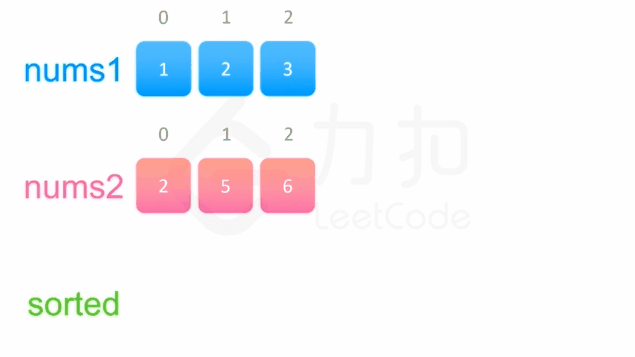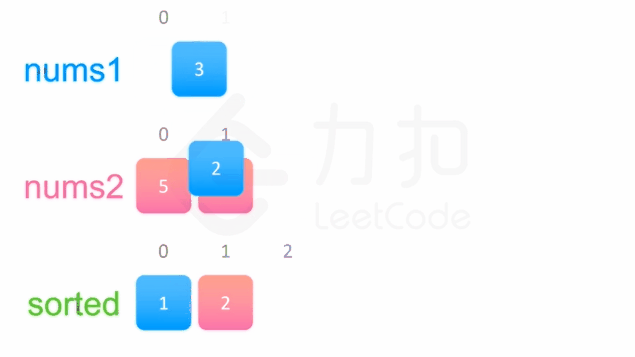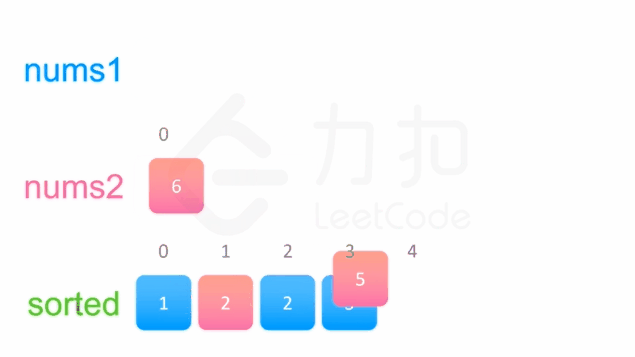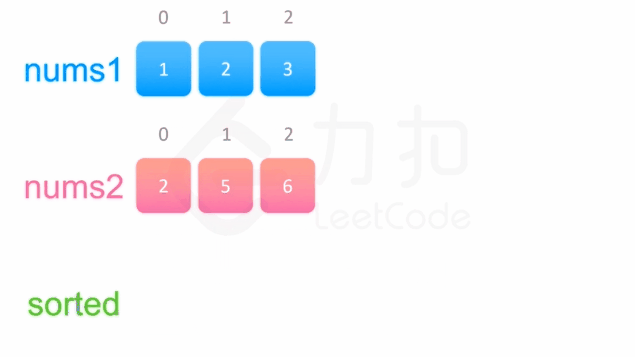
  我们为两个数组分别设置一个指针p1与p2来作为队列的头部指针。代码实现如下：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public void merge(int[] nums1, int m, int[] nums2, int n) { int p1 = 0, p2 = 0; int[] sorted = new int[m + n]; int cur; while (p1 < m || p2 < n) { if (p1 == m) { cur = nums2[p2++]; } else if (p2 == n) { cur = nums1[p1++]; } else if (nums1[p1] < nums2[p2]) { cur = nums1[p1++]; } else { cur = nums2[p2++]; } sorted[p1 + p2 - 1] = cur; } for (int i = 0; i != m + n; ++i) { nums1[i] = sorted[i]; } } }

day04

59. 螺旋矩阵 II

• 题目

  给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

  示例 1：

  

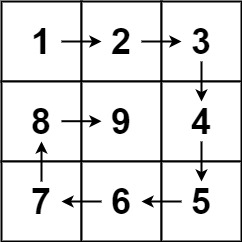
  1 2	输入：n = 3 输出：[[1,2,3],[8,9,4],[7,6,5]]

  示例 2：

  1 2	输入：n = 1 输出：[[1]]

  提示：

  • 1 <= n <= 20

• 方法一：暴力破解，环形遍历–>也即按层模拟

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  package other; import java.util.Arrays; class Solution5 { public static void main(String[] args) { System.out.println(Arrays.deepToString(generateMatrix(4))); } public static int[][] generateMatrix(int n) { int[][] arr = new int[n][n]; int val = 1;//表示填入值 int i = 0, j = 0;//arr数组索引，i为行标，j列标 int tempN1 = n;//表示每列或每行在某环的行走最大值 int tempN2 = 0;//表示每列或每行在某环的行走最小值 for (int l = 0; l < n - n / 2; l++) {//环数 while (j < tempN1) { arr[i][j] = val++; j++; } j--;//还原j值 i++;//下一个数 while (i < tempN1) { arr[i][j] = val++; i++; } i--;//还原i值 j--;//下一个数 while (j >= tempN2) { arr[i][j] = val++; j--; } j++;//还原j值 i--;//下一个数 while (i > tempN2) { arr[i][j] = val++; i--; } i++;//还原i数 j++;//指向下一个数字 tempN1--; tempN2++; } return arr; } }

day05

209. 长度最小的子数组

• 题目

  给定一个含有 n 个正整数的数组和一个正整数 target 。

  找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

• 方法一：暴力破解（超时）

  题目要求求出和大于等于target的长度最小的连续子数组，于是乎，就使用一个“窗口”从长度最小的1开始到整个数组的长度遍历，每次遍历都要“框出”子数组的和并比较，满足要求就返回。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

  public int minSubArrayLen(int target, int[] nums) { int left=0;//每个窗口的左索引 int sum=0; for(int cap=1;cap<=nums.length;cap++){//滑动窗口大小 for(left=0;left<nums.length-cap+1;left++){//左索引位置 sum=0; //计算窗口内的和 for(int i=left;i<left+cap;i++){ sum+=nums[i]; } if (sum>=target) return cap; } } return 0; }

• 方法二：滑动窗口

  使用左右指针 left 和 right，left 和 right 之间的长度即为滑动窗口的大小（即连续数组的大小）。如果滑动窗口内的值 sum >= target，维护连续数组最短长度，left 向右移动，缩小滑动窗口。如果滑动窗口内的值 sum < target，则 right 向有移动，扩大滑动窗口。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  public int minSubArrayLen(int target, int[] nums) { int left=0; int right=0; int sum=0; int len=Integer.MAX_VALUE; while(right<nums.length){ sum+=nums[right]; while(sum>=target){ if(len>right-left+1) len=right-left+1;//与上次的进行比较，保留最短结果 sum-=nums[left++]; } right++; } if (len==Integer.MAX_VALUE) return 0; return len; }

day06

977. 有序数组的平方

• 题目

  给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

  示例 1：

  1 2 3 4

  输入：nums = [-4,-1,0,3,10] 输出：[0,1,9,16,100] 解释：平方后，数组变为 [16,1,0,9,100] 排序后，数组变为 [0,1,9,16,100]

  示例2：

  1 2	输入：nums = [-7,-3,2,3,11] 输出：[4,9,9,49,121]

• 方法一：直接排序

  最简单的方法就是将数组nums中的数平方后直接排序。

  1 2 3 4 5 6 7 8 9 10

  class Solution { public int[] sortedSquares(int[] nums) { int[] ans = new int[nums.length]; for (int i = 0; i < nums.length; ++i) { ans[i] = nums[i] * nums[i]; } Arrays.sort(ans); return ans; } }

• 方法二：双指针

  同样地，我们可以使用两个指针分别指向位置 0 和 n-1，每次比较两个指针对应的数，选择较大的那个逆序放入答案并移动指针。这种方法无需处理某一指针移动至边界的情况，读者可以仔细思考其精髓所在。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  class Solution { public int[] sortedSquares(int[] nums) { int n = nums.length; int[] ans = new int[n]; for (int i = 0, j = n - 1, pos = n - 1; i <= j;) { if (nums[i] * nums[i] > nums[j] * nums[j]) { ans[pos] = nums[i] * nums[i]; ++i; } else { ans[pos] = nums[j] * nums[j]; --j; } --pos; } return ans; } }

day07

19. 删除链表的倒数第 N 个结点

• 题目

  给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

  示例 1：

  

  1 2	输入：head = [1,2,3,4,5], n = 2 输出：[1,2,3,5]

  示例 2：

  1 2	输入：head = [1], n = 1 输出：[]

  示例 3：

  1 2	输入：head = [1,2], n = 1 输出：[1]

  提示：

  • 链表中结点的数目为 sz
  • 1 <= sz <= 30
  • 0 <= Node.val <= 100
  • 1 <= n <= sz

  **进阶：**你能尝试使用一趟扫描实现吗？

• 解决思路

  前言

  在对链表进行操作时，一种常用的技巧是添加一个哑节点（dummy node），它的 next 指针指向链表的头节点。这样一来，我们就不需要对头节点进行特殊的判断了。

  例如，在本题中，如果我们要删除节点 y，我们需要知道节点 y 的前驱节点 x，并将 x 的指针指向 y 的后继节点。但由于头节点不存在前驱节点，因此我们需要在删除头节点时进行特殊判断。但如果我们添加了哑节点，那么头节点的前驱节点就是哑节点本身，此时我们就只需要考虑通用的情况即可。（注意：此处头节点存放了有意义的数据）

  特别地，在某些语言中，由于需要自行对内存进行管理。因此在实际的面试中，对于「是否需要释放被删除节点对应的空间」这一问题，我们需要和面试官进行积极的沟通以达成一致。下面的代码中默认不释放空间。

  方法一：计算链表长度

  思路与算法

  一种容易想到的方法是，我们首先从头节点开始对链表进行一次遍历，得到链表的长度 LL。随后我们再从头节点开始对链表进行一次遍历，当遍历到第 L-n+1个节点时，它就是我们需要删除的节点。

  为了与题目中的 n 保持一致，节点的编号从 1 开始，头节点为编号 1 的节点。

  为了方便删除操作，我们可以从哑节点开始遍历 L-n+1个节点。当遍历到第 L-n+1 个节点时，它的下一个节点就是我们需要删除的节点，这样我们只需要修改一次指针，就能完成删除操作。

  

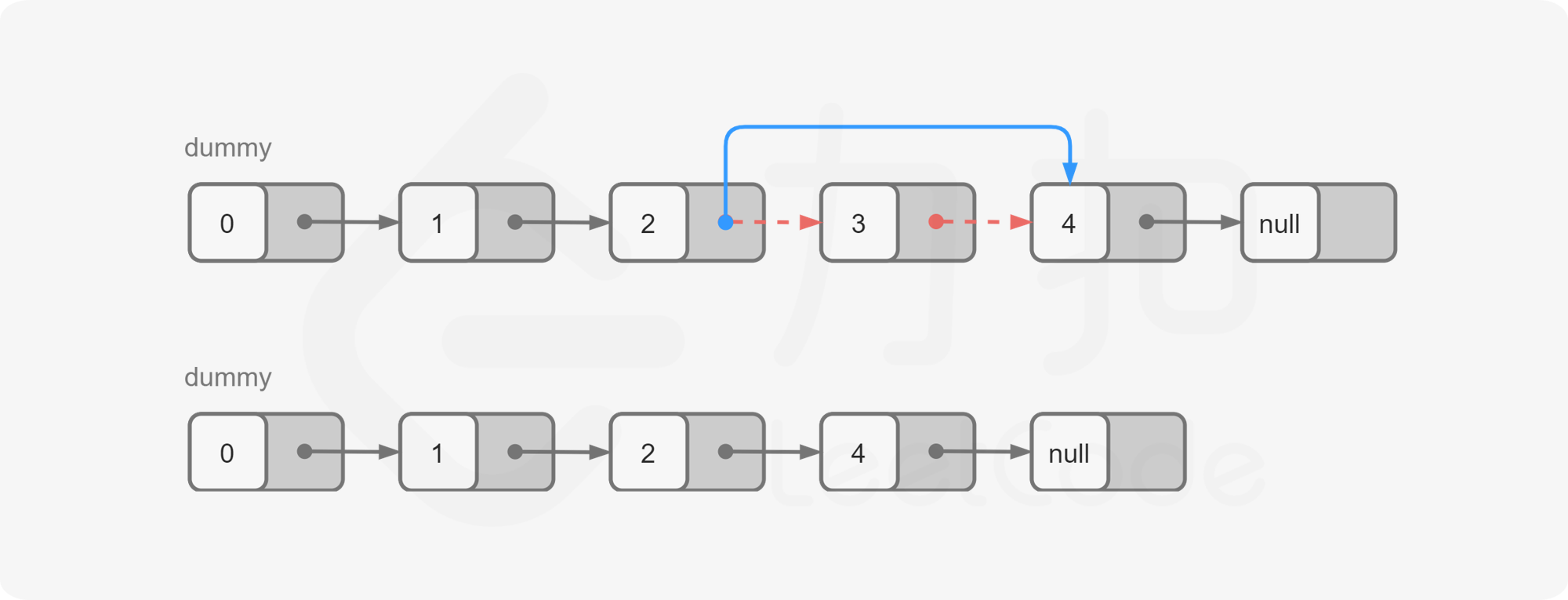
  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public ListNode removeNthFromEnd(ListNode head, int n) { ListNode dummy = new ListNode(0, head); int length = getLength(head); ListNode cur = dummy; for (int i = 1; i < length - n + 1; ++i) { cur = cur.next; } cur.next = cur.next.next; ListNode ans = dummy.next; return ans; } public int getLength(ListNode head) { int length = 0; while (head != null) { ++length; head = head.next; } return length; } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  /** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func removeNthFromEnd(head *ListNode, n int) *ListNode { l:=0 heads:=&ListNode{Next:head} tmp:=heads for tmp!=nil{ l++ tmp=tmp.Next } tmp = heads no:=0 for tmp!=nil { // 找到了n节点 if no==l-n-1 { if tmp.Next!=nil{ tmp.Next = tmp.Next.Next }else{ tmp.Next = nil } } no++ tmp=tmp.Next } return heads.Next }

  复杂度分析

  • 时间复杂度：O(L)，其中 L是链表的长度。
  • 空间复杂度：O(1)。

  方法二：栈

  思路与算法

  我们也可以在遍历链表的同时将所有节点依次入栈。根据栈「先进后出」的原则，我们弹出栈的第 n 个节点就是需要删除的节点，并且目前栈顶的节点就是待删除节点的前驱节点。这样一来，删除操作就变得十分方便了。

  

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public ListNode removeNthFromEnd(ListNode head, int n) { ListNode dummy = new ListNode(0, head); Deque<ListNode> stack = new LinkedList<ListNode>(); ListNode cur = dummy; while (cur != null) { stack.push(cur); cur = cur.next; } for (int i = 0; i < n; ++i) { stack.pop(); } ListNode prev = stack.peek(); prev.next = prev.next.next; ListNode ans = dummy.next; return ans; } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  /** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func removeNthFromEnd(head *ListNode, n int) *ListNode { heads:=&ListNode{Next:head} stack := []*ListNode{} // 先所有节点入栈 tmp:=heads for tmp!=nil { stack = append(stack,tmp) tmp = tmp.Next } var lastN *ListNode for n>0{ lastN = stack[len(stack)-1] stack = stack[:len(stack)-1] n-- } stack[len(stack)-1].Next = lastN.Next return heads.Next }

  复杂度分析

  • 时间复杂度：O(L)，其中 L 是链表的长度。
  • 空间复杂度：O(L)，其中 L 是链表的长度。主要为栈的开销。

  方法三：双指针

  思路与算法

  我们也可以在不预处理出链表的长度，以及使用常数空间的前提下解决本题。

  由于我们需要找到倒数第 n 个节点，因此我们可以使用两个指针first 和 second 同时对链表进行遍历，并且 first 比 second 超前 n 个节点。当 first 遍历到链表的末尾时，second 就恰好处于倒数第 n 个节点。

  具体地，初始时 first 和second 均指向头节点。我们首先使用first 对链表进行遍历，遍历的次数为 n。此时，first 和 second 之间间隔了 n-1个节点，即first 比 second 超前了 n个节点。

  在这之后，我们同时使用 first和 second 对链表进行遍历。当first 遍历到链表的末尾（即first 为空指针）时，second 恰好指向倒数第 n 个节点。

  根据方法一和方法二，如果我们能够得到的是倒数第 n 个节点的前驱节点而不是倒数第 n 个节点的话，删除操作会更加方便。因此我们可以考虑在初始时将 second 指向哑节点，其余的操作步骤不变。这样一来，当 first 遍历到链表的末尾时，second 的下一个节点就是我们需要删除的节点。

  

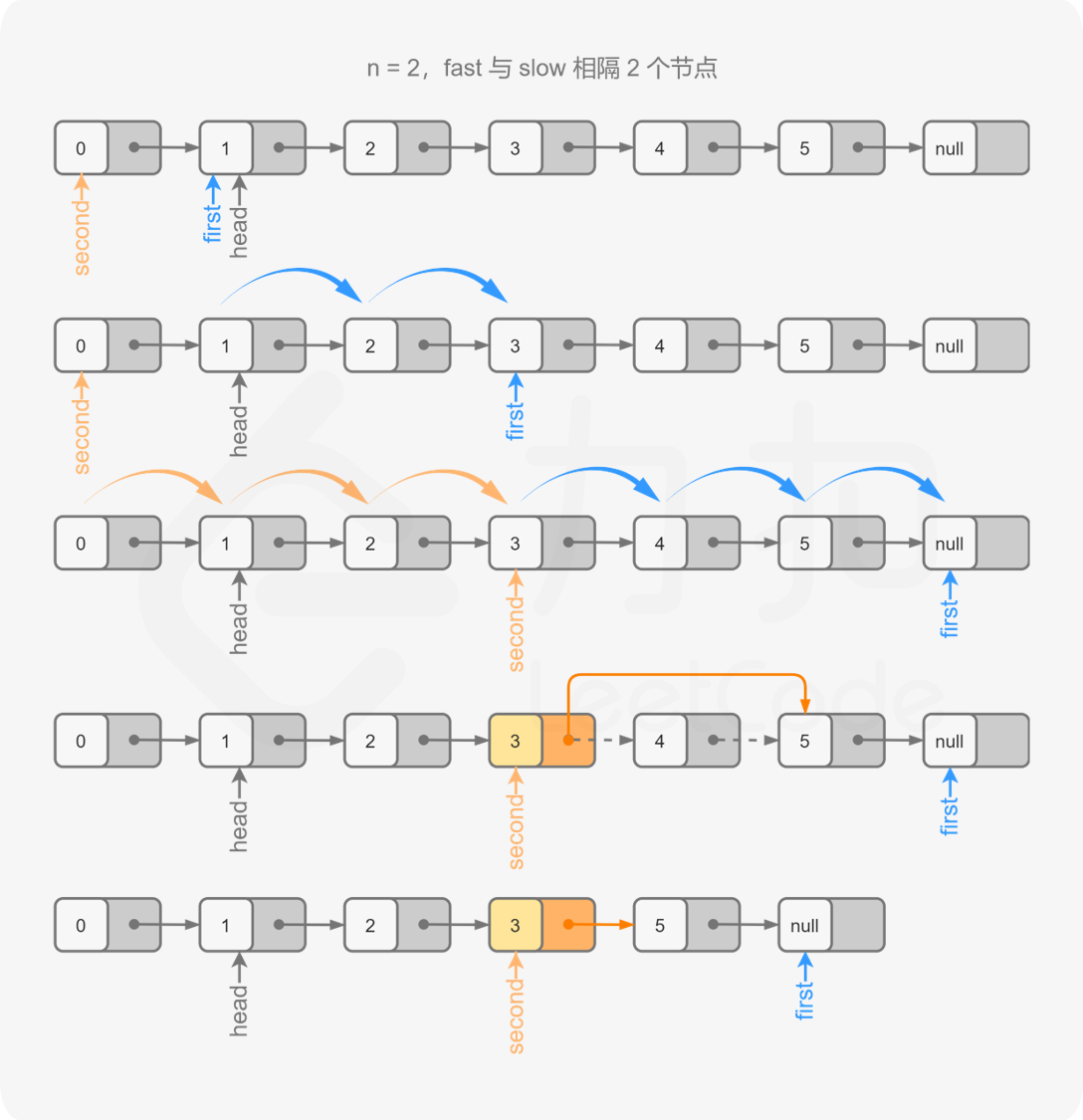
  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  class Solution { public ListNode removeNthFromEnd(ListNode head, int n) { ListNode dummy = new ListNode(0, head); ListNode first = head; ListNode second = dummy; for (int i = 0; i < n; ++i) { first = first.next; } while (first != null) { first = first.next; second = second.next; } second.next = second.next.next; ListNode ans = dummy.next; return ans; } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  /** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func removeNthFromEnd(head *ListNode, n int) *ListNode { heads:=&ListNode{Next:head} first:=heads second:=heads for n>0 { first = first.Next n-- } for first.Next!=nil{ first=first.Next second = second.Next } // fmt.Println(second.Val) second.Next = second.Next.Next return heads.Next }

  复杂度分析

  • 时间复杂度：O(L)，其中 L 是链表的长度。
  • 空间复杂度：O(1)。

day08

24. 两两交换链表中的节点

• 题目

  给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

  示例 1：

  

  1 2	输入：head = [1,2,3,4] 输出：[2,1,4,3]

  示例 2：

  1 2	输入：head = [] 输出：[]

  示例 3：

  1 2	输入：head = [1] 输出：[1]

  提示：

  • 链表中节点的数目在范围 [0, 100] 内
  • 0 <= Node.val <= 100

• 方法

  方法一：递归

  思路与算法

  可以通过递归的方式实现两两交换链表中的节点。

  递归的终止条件是链表中没有节点，或者链表中只有一个节点，此时无法进行交换。

  如果链表中至少有两个节点，则在两两交换链表中的节点之后，原始链表的头节点变成新的链表的第二个节点，原始链表的第二个节点变成新的链表的头节点。链表中的其余节点的两两交换可以递归地实现。在对链表中的其余节点递归地两两交换之后，更新节点之间的指针关系，即可完成整个链表的两两交换。

  用 head 表示原始链表的头节点，新的链表的第二个节点，用 newHead 表示新的链表的头节点，原始链表的第二个节点，则原始链表中的其余节点的头节点是 newHead.next。令 head.next = swapPairs(newHead.next)，表示将其余节点进行两两交换，交换后的新的头节点为 head 的下一个节点。然后令 newHead.next = head，即完成了所有节点的交换。最后返回新的链表的头节点 newHead。

  代码

  1 2 3 4 5 6 7 8 9 10 11

  class Solution { public ListNode swapPairs(ListNode head) { if (head == null || head.next == null) { return head; } ListNode newHead = head.next; head.next = swapPairs(newHead.next); newHead.next = head; return newHead; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是链表的节点数量。需要对每个节点进行更新指针的操作。
  • 空间复杂度：O(n)，其中 n 是链表的节点数量。空间复杂度主要取决于递归调用的栈空间。

  方法二：迭代

  思路与算法

  也可以通过迭代的方式实现两两交换链表中的节点。

  创建哑结点 dummyHead，令 dummyHead.next = head。令 temp 表示当前到达的节点，初始时 temp = dummyHead。每次需要交换 temp 后面的两个节点。

  如果 temp 的后面没有节点或者只有一个节点，则没有更多的节点需要交换，因此结束交换。否则，获得 temp 后面的两个节点 node1 和 node2，通过更新节点的指针关系实现两两交换节点。

  具体而言，交换之前的节点关系是 temp -> node1 -> node2，交换之后的节点关系要变成 temp -> node2 -> node1，因此需要进行如下操作。

  1 2 3

  temp.next = node2 node1.next = node2.next node2.next = node1

  完成上述操作之后，节点关系即变成 temp -> node2 -> node1。再令 temp = node1，对链表中的其余节点进行两两交换，直到全部节点都被两两交换。

  两两交换链表中的节点之后，新的链表的头节点是 dummyHead.next，返回新的链表的头节点即可。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52

  class Solution { public ListNode swapPairs(ListNode head) { ListNode dummyHead = new ListNode(0); dummyHead.next = head; ListNode temp = dummyHead; while (temp.next != null && temp.next.next != null) { ListNode node1 = temp.next; ListNode node2 = temp.next.next; temp.next = node2; node1.next = node2.next; node2.next = node1; temp = node1; } return dummyHead.next; } } //the other /** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode() {} * ListNode(int val) { this.val = val; } * ListNode(int val, ListNode next) { this.val = val; this.next = next; } * } */ class Solution { public ListNode swapPairs(ListNode head) { //哑节点 ListNode dummyNode = new ListNode(-1,head); //每两个节点的遍历链表，当不足两个时则不交换 ListNode temp=dummyNode; ListNode pre=temp.next; if(temp.next==null){ return dummyNode.next; } ListNode post=temp.next.next; while(pre!=null&&post!=null){ temp.next=post; pre.next=post.next; post.next=pre; //移动指针 temp=pre; pre=temp.next; if(temp.next!=null){ post=temp.next.next; } } return dummyNode.next; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是链表的节点数量。需要对每个节点进行更新指针的操作。
  • 空间复杂度：O(1)。

day09

25. K 个一组翻转链表

• 题目

  给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

  k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

  你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

  示例 1：

  

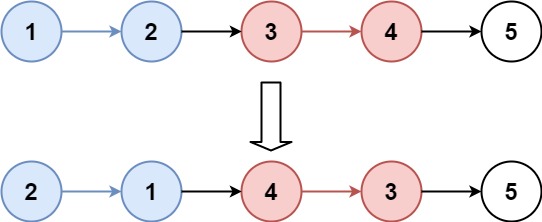
  1 2	输入：head = [1,2,3,4,5], k = 2 输出：[2,1,4,3,5]

  示例 2：

  

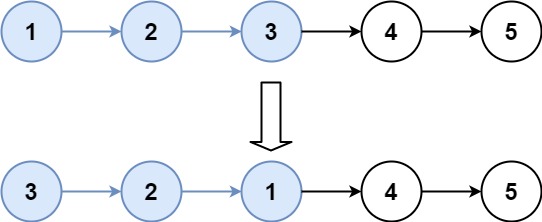
  1 2	输入：head = [1,2,3,4,5], k = 3 输出：[3,2,1,4,5]

  提示：

  • 链表中的节点数目为 n
  • 1 <= k <= n <= 5000
  • 0 <= Node.val <= 1000

  **进阶：**你可以设计一个只用 O(1) 额外内存空间的算法解决此问题吗？

• 方法

  方法一：模拟

  思路与算法

  本题的目标非常清晰易懂，不涉及复杂的算法，但是实现过程中需要考虑的细节比较多，容易写出冗长的代码。主要考查面试者设计的能力。

  我们需要把链表节点按照 k 个一组分组，所以可以使用一个指针 head 依次指向每组的头节点。这个指针每次向前移动 k 步，直至链表结尾。对于每个分组，我们先判断它的长度是否大于等于 k。若是，我们就翻转这部分链表，否则不需要翻转。

  接下来的问题就是如何翻转一个分组内的子链表。翻转一个链表并不难，过程可以参考「206. 反转链表」。但是对于一个子链表，除了翻转其本身之外，还需要将子链表的头部与上一个子链表连接，以及子链表的尾部与下一个子链表连接。如下图所示：

  

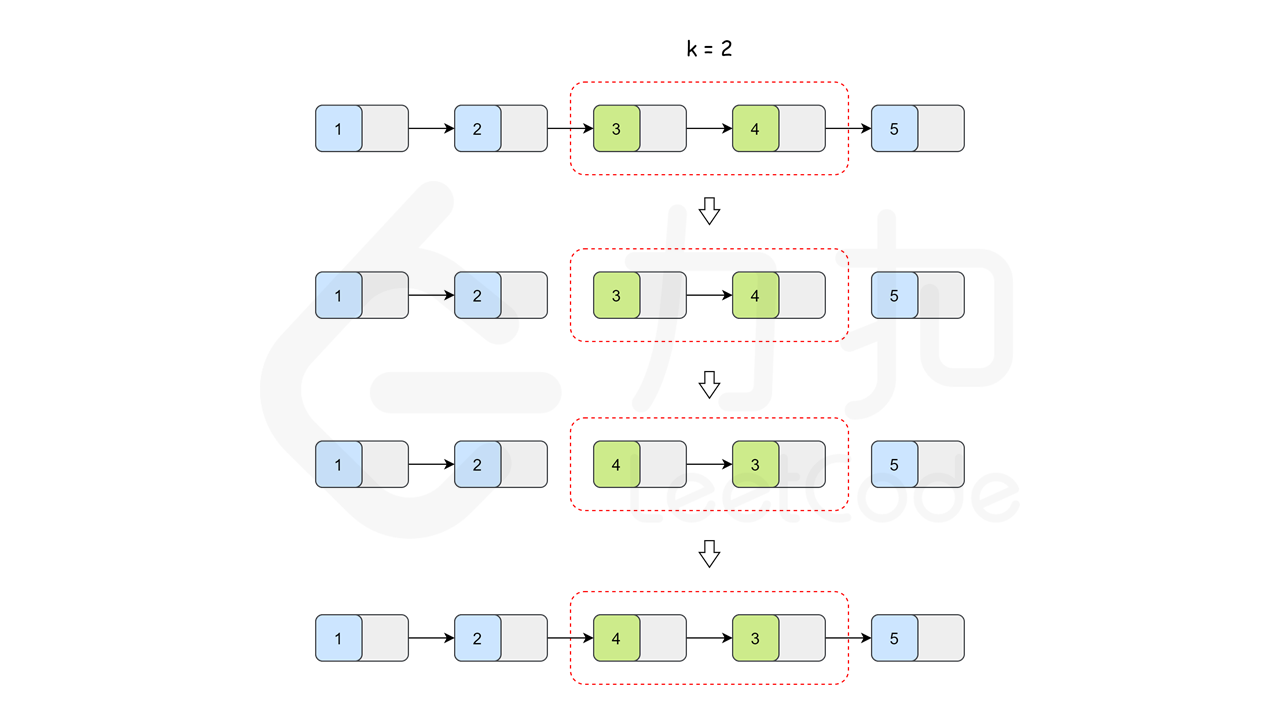
  因此，在翻转子链表的时候，我们不仅需要子链表头节点 head，还需要有 head 的上一个节点 pre，以便翻转完后把子链表再接回 pre。

  但是对于第一个子链表，它的头节点 head 前面是没有节点 pre 的。太麻烦了！难道只能特判了吗？答案是否定的。没有条件，我们就创造条件；没有节点，我们就创建一个节点。我们新建一个节点（哑节点），把它接到链表的头部，让它作为 pre 的初始值，这样 head 前面就有了一个节点，我们就可以避开链表头部的边界条件。这么做还有一个好处，下面我们会看到。

  反复移动指针 head 与 pre，对 head 所指向的子链表进行翻转，直到结尾，我们就得到了答案。下面我们该返回函数值了。

  有的同学可能发现这又是一件麻烦事：链表翻转之后，链表的头节点发生了变化，那么应该返回哪个节点呢？照理来说，前 k 个节点翻转之后，链表的头节点应该是第 k 个节点。那么要在遍历过程中记录第 k 个节点吗？但是如果链表里面没有 k 个节点，答案又还是原来的头节点。我们又多了一大堆循环和判断要写，太崩溃了！

  等等！还记得我们创建了节点 pre 吗？这个节点一开始被连接到了头节点的前面，而无论之后链表有没有翻转，它的 next 指针都会指向正确的头节点。那么我们只要返回它的下一个节点就好了。至此，问题解决。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41

  class Solution { public ListNode reverseKGroup(ListNode head, int k) { ListNode hair = new ListNode(0); hair.next = head; ListNode pre = hair; while (head != null) { ListNode tail = pre; // 查看剩余部分长度是否大于等于 k for (int i = 0; i < k; ++i) { tail = tail.next; if (tail == null) { return hair.next; } } ListNode nex = tail.next; ListNode[] reverse = myReverse(head, tail); head = reverse[0]; tail = reverse[1]; // 把子链表重新接回原链表 pre.next = head; tail.next = nex; pre = tail; head = tail.next; } return hair.next; } public ListNode[] myReverse(ListNode head, ListNode tail) { ListNode prev = tail.next; ListNode p = head; while (prev != tail) { ListNode nex = p.next; p.next = prev; prev = p; p = nex; } return new ListNode[]{tail, head}; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为链表的长度。head 指针会在 $O(\lfloor \frac{n}{k} \rfloor) $个节点上停留，每次停留需要进行一次 O(k) 的翻转操作。
  • 空间复杂度：O(1)，我们只需要建立常数个变量。

day10

141. 环形链表

• 题目

  给你一个链表的头节点 head ，判断链表中是否有环。

  如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

  如果链表中存在环 ，则返回 true 。 否则，返回 false 。

  示例 1：

  

  1 2 3

  输入：head = [3,2,0,-4], pos = 1 输出：true 解释：链表中有一个环，其尾部连接到第二个节点。

  示例 2：

  

  1 2 3

  输入：head = [1,2], pos = 0 输出：true 解释：链表中有一个环，其尾部连接到第一个节点。

  示例 3：

  

  1 2 3

  输入：head = [1], pos = -1 输出：false 解释：链表中没有环。

  提示：

  • 链表中节点的数目范围是 [0, 104]
  • -105 <= Node.val <= 105
  • pos 为 -1 或者链表中的一个 有效索引 。

  **进阶：**你能用 O(1)（即，常量）内存解决此问题吗？

• 解法

  方法一：哈希表

  思路及算法

  最容易想到的方法是遍历所有节点，每次遍历到一个节点时，判断该节点此前是否被访问过。

  具体地，我们可以使用哈希表来存储所有已经访问过的节点。每次我们到达一个节点，如果该节点已经存在于哈希表中，则说明该链表是环形链表，否则就将该节点加入哈希表中。重复这一过程，直到我们遍历完整个链表即可。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12

  public class Solution { public boolean hasCycle(ListNode head) { Set<ListNode> seen = new HashSet<ListNode>(); while (head != null) { if (!seen.add(head)) { return true; } head = head.next; } return false; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 是链表中的节点数。最坏情况下我们需要遍历每个节点一次。
  • 空间复杂度：O(N)，其中 N 是链表中的节点数。主要为哈希表的开销，最坏情况下我们需要将每个节点插入到哈希表中一次。

  方法二：快慢指针

  思路及算法

  本方法需要读者对「Floyd 判圈算法」（又称龟兔赛跑算法）有所了解。

  假想「乌龟」和「兔子」在链表上移动，「兔子」跑得快，「乌龟」跑得慢。当「乌龟」和「兔子」从链表上的同一个节点开始移动时，如果该链表中没有环，那么「兔子」将一直处于「乌龟」的前方；如果该链表中有环，那么「兔子」会先于「乌龟」进入环，并且一直在环内移动。等到「乌龟」进入环时，由于「兔子」的速度快，它一定会在某个时刻与乌龟相遇，即套了「乌龟」若干圈。

  我们可以根据上述思路来解决本题。具体地，我们定义两个指针，一快一满。慢指针每次只移动一步，而快指针每次移动两步。初始时，慢指针在位置 head，而快指针在位置 head.next。这样一来，如果在移动的过程中，快指针反过来追上慢指针，就说明该链表为环形链表。否则快指针将到达链表尾部，该链表不为环形链表。

  细节

  为什么我们要规定初始时慢指针在位置 head，快指针在位置 head.next，而不是两个指针都在位置 head（即与「乌龟」和「兔子」中的叙述相同）？

  • 观察下面的代码，我们使用的是 while 循环，循环条件先于循环体。由于循环条件一定是判断快慢指针是否重合，如果我们将两个指针初始都置于 head，那么 while 循环就不会执行。因此，我们可以假想一个在 head 之前的虚拟节点，慢指针从虚拟节点移动一步到达 head，快指针从虚拟节点移动两步到达 head.next，这样我们就可以使用 while 循环了。
  • 当然，我们也可以使用 do-while 循环。此时，我们就可以把快慢指针的初始值都置为 head。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  public class Solution { public boolean hasCycle(ListNode head) { if (head == null || head.next == null) { return false; } ListNode slow = head; ListNode fast = head.next; while (slow != fast) { if (fast == null || fast.next == null) { return false; } slow = slow.next; fast = fast.next.next; } return true; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 是链表中的节点数。
    • 当链表中不存在环时，快指针将先于慢指针到达链表尾部，链表中每个节点至多被访问两次。
    • 当链表中存在环时，每一轮移动后，快慢指针的距离将减小一。而初始距离为环的长度，因此至多移动 N 轮。
  • 空间复杂度：O(1)。我们只使用了两个指针的额外空间。

day11

142. 环形链表 II

• 题目

  给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

  如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

  不允许修改 链表。

  示例 1：

  

  1 2 3

  输入：head = [3,2,0,-4], pos = 1 输出：返回索引为 1 的链表节点 解释：链表中有一个环，其尾部连接到第二个节点。

  示例 2：

  

  1 2 3

  输入：head = [1,2], pos = 0 输出：返回索引为 0 的链表节点 解释：链表中有一个环，其尾部连接到第一个节点。

  示例 3：

  

  1 2 3

  输入：head = [1], pos = -1 输出：返回 null 解释：链表中没有环。

  提示：

  • 链表中节点的数目范围在范围 [0, 104] 内
  • -105 <= Node.val <= 105
  • pos 的值为 -1 或者链表中的一个有效索引

  **进阶：**你是否可以使用 O(1) 空间解决此题？

• 方法

  方法一：哈希表

  思路与算法

  一个非常直观的思路是：我们遍历链表中的每个节点，并将它记录下来；一旦遇到了此前遍历过的节点，就可以判定链表中存在环。借助哈希表可以很方便地实现。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

  public class Solution { public ListNode detectCycle(ListNode head) { ListNode pos = head; Set<ListNode> visited = new HashSet<ListNode>(); while (pos != null) { if (visited.contains(pos)) { return pos; } else { visited.add(pos); } pos = pos.next; } return null; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 为链表中节点的数目。我们恰好需要访问链表中的每一个节点。

    空间复杂度：O(N)，其中 N 为链表中节点的数目。我们需要将链表中的每个节点都保存在哈希表当中。

  方法二：快慢指针

  思路与算法

  我们使用两个指针，fast 与 slow。它们起始都位于链表的头部。随后，slow 指针每次向后移动一个位置，而 fast 指针向后移动两个位置。如果链表中存在环，则 fast 指针最终将再次与 slow 指针在环中相遇。

  如下图所示，设链表中环外部分的长度为 a。slow 指针进入环后，又走了 b 的距离与 fast 相遇。此时，fast 指针已经走完了环的 n 圈，因此它走过的总距离为 a+n*(b+c)+b = a+(n+1)*b+n*c。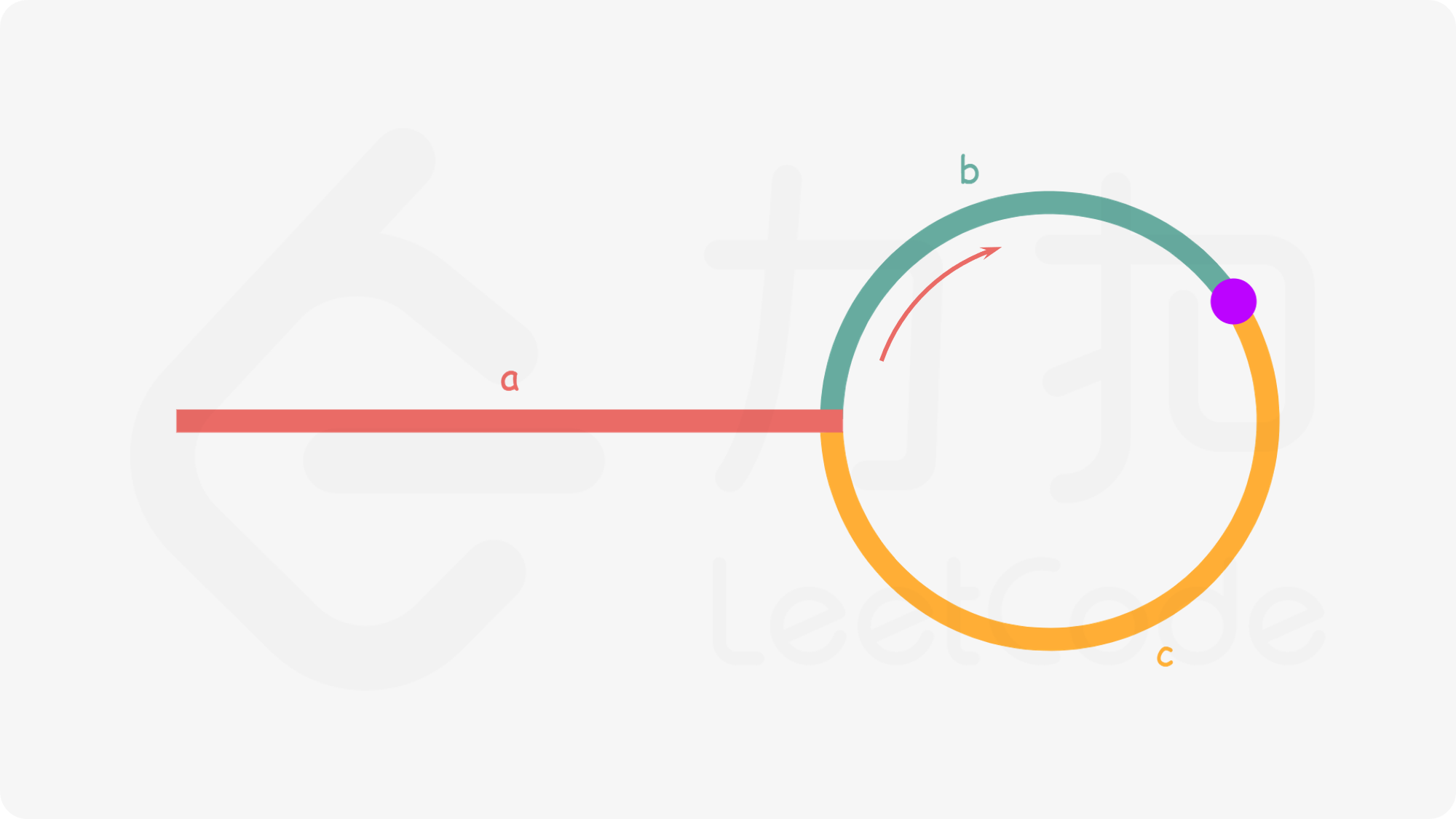

  

  根据题意，任意时刻，fast 指针走过的距离都为 slow 指针的 2 倍。因此，我们有

    						`a+(n+1)*b+n*c = 2*(a+b) ==> a = c+(n-1)*(b+c)`
  

  有了 a=c+(n-1)(b+c) 的等量关系，我们会发现：从相遇点到入环点的距离加上 n-1 圈的环长，恰好等于从链表头部到入环点的距离。

  因此，当发现 slow 与 fast 相遇时，我们再额外使用一个指针 ptr。起始，它指向链表头部；随后，它和 slow 每次向后移动一个位置。最终，它们会在入环点相遇。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  public class Solution { public ListNode detectCycle(ListNode head) { if (head == null) { return null; } ListNode slow = head, fast = head; while (fast != null) { slow = slow.next; if (fast.next != null) { fast = fast.next.next; } else { return null; } if (fast == slow) { ListNode ptr = head; while (ptr != slow) { ptr = ptr.next; slow = slow.next; } return ptr; } } return null; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 为链表中节点的数目。在最初判断快慢指针是否相遇时，slow 指针走过的距离不会超过链表的总长度；随后寻找入环点时，走过的距离也不会超过链表的总长度。因此，总的执行时间为 O(N)+O(N)=O(N)。
  • 空间复杂度：O(1)。我们只使用了 slow,fast,ptr 三个指针。

day12

160. 相交链表

• 题目

  给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

  图示两个链表在节点 c1 开始相交**：**

  

  题目数据 保证 整个链式结构中不存在环。

  注意，函数返回结果后，链表必须 保持其原始结构 。

  自定义评测：

  评测系统 的输入如下（你设计的程序 不适用 此输入）：

  • intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
  • listA - 第一个链表
  • listB - 第二个链表
  • skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
  • skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

  评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

  示例 1：

  

  1 2 3 4 5

  输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 输出：Intersected at '8' 解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。 从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。 在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。

  示例 2：

  

  1 2 3 4 5

  输入：intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出：Intersected at '2' 解释：相交节点的值为 2 （注意，如果两个链表相交则不能为 0）。 从各自的表头开始算起，链表 A 为 [1,9,1,2,4]，链表 B 为 [3,2,4]。 在 A 中，相交节点前有 3 个节点；在 B 中，相交节点前有 1 个节点。

  示例 3：

  

  1 2 3 4 5

  输入：intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出：null 解释：从各自的表头开始算起，链表 A 为 [2,6,4]，链表 B 为 [1,5]。 由于这两个链表不相交，所以 intersectVal 必须为 0，而 skipA 和 skipB 可以是任意值。 这两个链表不相交，因此返回 null 。

  提示：

  • listA 中节点数目为 m
  • listB 中节点数目为 n
  • 1 <= m, n <= 3 * 104
  • 1 <= Node.val <= 105
  • 0 <= skipA <= m
  • 0 <= skipB <= n
  • 如果 listA 和 listB 没有交点，intersectVal 为 0
  • 如果 listA 和 listB 有交点，intersectVal == listA[skipA] == listB[skipB]

  **进阶：**你能否设计一个时间复杂度 O(m + n) 、仅用 O(1) 内存的解决方案？

• 方法

  方法一：哈希集合

  思路和算法

  判断两个链表是否相交，可以使用哈希集合存储链表节点。

  首先遍历链表 headA，并将链表 headA 中的每个节点加入哈希集合中。然后遍历链表 headB，对于遍历到的每个节点，判断该节点是否在哈希集合中：

  • 如果当前节点不在哈希集合中，则继续遍历下一个节点；
  • 如果当前节点在哈希集合中，则后面的节点都在哈希集合中，即从当前节点开始的所有节点都在两个链表的相交部分，因此在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点，返回该节点。

  如果链表 headB 中的所有节点都不在哈希集合中，则两个链表不相交，返回 null。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  public class Solution { public ListNode getIntersectionNode(ListNode headA, ListNode headB) { Set<ListNode> visited = new HashSet<ListNode>(); ListNode temp = headA; while (temp != null) { visited.add(temp); temp = temp.next; } temp = headB; while (temp != null) { if (visited.contains(temp)) { return temp; } temp = temp.next; } return null; } }

  复杂度分析

  • 时间复杂度：O(m+n)，其中 m 和 n 是分别是链表 headA 和 headB 的长度。需要遍历两个链表各一次。
  • 空间复杂度：O(m)，其中 m 是链表 headA 的长度。需要使用哈希集合存储链表 headA 中的全部节点。

  方法二：双指针

  思路和算法

  使用双指针的方法，可以将空间复杂度降至 O(1)O(1)。

  只有当链表 headA 和 headB 都不为空时，两个链表才可能相交。因此首先判断链表 headA 和 headB 是否为空，如果其中至少有一个链表为空，则两个链表一定不相交，返回 null。

  当链表 headA 和 headB 都不为空时，创建两个指针 pA 和 pB*，初始时分别指向两个链表的头节点 headA 和 headB，然后将两个指针依次遍历两个链表的每个节点。具体做法如下：

  • 每步操作需要同时更新指针 pA 和 pB。
  • 如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针 pB 不为空，则将指针 pB 移到下一个节点。
  • 如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。
  • 当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 null。

  证明

  下面提供双指针方法的正确性证明。考虑两种情况，第一种情况是两个链表相交，第二种情况是两个链表不相交。

  情况一：两个链表相交

  链表 headA 和 headB 的长度分别是 m 和 n*。假设链表 headA 的不相交部分有 a 个节点，链表 headB 的不相交部分有 b 个节点，两个链表相交的部分有 c 个节点，则有 a+c=m，b+c=n。

  • 如果 a=b，则两个指针会同时到达两个链表相交的节点，此时返回相交的节点；
  • 如果 a!=b，则指针 pA 会遍历完链表 headA，指针 pB 会遍历完链表 headB，两个指针不会同时到达链表的尾节点，然后指针 pA 移到链表 headB 的头节点，指针 pB 移到链表 headA 的头节点，然后两个指针继续移动，在指针 pA 移动了 a+c+b 次、指针 pB 移动了 b+c+a 次之后，两个指针会同时到达两个链表相交的节点，该节点也是两个指针第一次同时指向的节点，此时返回相交的节点。

  情况二：两个链表不相交

  链表 headA 和 headB 的长度分别是 m 和 n。考虑当 m=n 和 m != n 时，两个指针分别会如何移动：

  • 如果 m=n，则两个指针会同时到达两个链表的尾节点，然后同时变成空值 null，此时返回 null；
  • 如果 m != n，则由于两个链表没有公共节点，两个指针也不会同时到达两个链表的尾节点，因此两个指针都会遍历完两个链表，在指针 pA 移动了 m+n 次、指针 pB 移动了 n+m 次之后，两个指针会同时变成空值 null，此时返回 null。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13

  public class Solution { public ListNode getIntersectionNode(ListNode headA, ListNode headB) { if (headA == null || headB == null) { return null; } ListNode pA = headA, pB = headB; while (pA != pB) { pA = pA == null ? headB : pA.next; pB = pB == null ? headA : pB.next; } return pA; } }

  复杂度分析

  • 时间复杂度：O(m+n)，其中 m 和 n 是分别是链表 headA 和 headB 的长度。两个指针同时遍历两个链表，每个指针遍历两个链表各一次。
  • 空间复杂度：O(1)。

day13

206. 反转链表

• 题目

  给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

  示例 1：

  

  1 2	输入：head = [1,2,3,4,5] 输出：[5,4,3,2,1]

  示例 2：

  

  1 2	输入：head = [1,2] 输出：[2,1]

  示例 3：

  1 2	输入：head = [] 输出：[]

  提示：

  • 链表中节点的数目范围是 [0, 5000]
  • -5000 <= Node.val <= 5000

• 解法

  方法一：迭代

  假设存在链表 1–>2–>3–>∅，我们想要把它改成 ∅<–1<–2<–3。

  在遍历列表时，将当前节点的 next 指针改为指向前一个元素。由于节点没有引用其上一个节点，因此必须事先存储其前一个元素。在更改引用之前，还需要另一个指针来存储下一个节点。不要忘记在最后返回新的头引用！

  1 2 3 4 5 6 7 8 9 10 11 12 13

  class Solution { public ListNode reverseList(ListNode head) { ListNode prev = null; ListNode curr = head; while (curr != null) { ListNode nextTemp = curr.next; curr.next = prev; prev = curr; curr = nextTemp; } return prev; } }

  复杂度分析

  • 时间复杂度：O(n)，假设 n 是列表的长度，时间复杂度是 O(n)。
  • 空间复杂度：O(1)。

  方法二：递归

  递归版本稍微复杂一些，其关键在于反向工作。假设列表的其余部分已经被反转，现在我们应该如何反转它前面的部分？

  假设列表为：

    					n~1~-->…-->n~k−1~-->n~k~-->n~k+1~-->…-->n~m~-->∅
  

  若从节点 n~k+1~ 到 n~k~

    					n~1~-->…-->n~k−1~-->n~k~-->n~k+1~<--…<--n~m~
  

  我们希望 n~k+1~ 的下一个节点指向 n~k~

  所以，n~k~.next.next*=*n~k~

  要小心的是 n~1~ 的下一个必须指向 ∅ 。如果你忽略了这一点，你的链表中可能会产生循环。如果使用大小为 22 的链表测试代码，则可能会捕获此错误。

  1 2 3 4 5 6 7 8 9 10 11

  class Solution { public ListNode reverseList(ListNode head) { if (head == null || head.next == null) { return head; } ListNode p = reverseList(head.next); head.next.next = head; head.next = null; return p; } }

  复杂度分析

  • 时间复杂度：O(n)，假设 n 是列表的长度，那么时间复杂度为 O(n)。
  • 空间复杂度：O(n)，由于使用递归，将会使用隐式栈空间。递归深度可能会达到 n 层。

day14

20. 有效的括号

• 题目

  给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串 s ，判断字符串是否有效。

  有效字符串需满足：

  1. 左括号必须用相同类型的右括号闭合。
  2. 左括号必须以正确的顺序闭合。

  示例 1：

  1 2	输入：s = "()" 输出：true

  示例 2：

  1 2	输入：s = "()[]{}" 输出：true

  示例 3：

  1 2	输入：s = "(]" 输出：false

  示例 4：

  1 2	输入：s = "([)]" 输出：false

  示例 5：

  1 2	输入：s = "{[]}" 输出：true

  提示：

  • 1 <= s.length <= 104
  • s 仅由括号 '()[]{}' 组成

• 题解

  方法一：栈

  判断括号的有效性可以使用「栈」这一数据结构来解决。

  我们遍历给定的字符串 s。当我们遇到一个左括号时，我们会期望在后续的遍历中，有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合，因此我们可以将这个左括号放入栈顶。

  当我们遇到一个右括号时，我们需要将一个相同类型的左括号闭合。此时，我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型，或者栈中并没有左括号，那么字符串 s 无效，返回 False。为了快速判断括号的类型，我们可以使用哈希表存储每一种括号。哈希表的键为右括号，值为相同类型的左括号。

  在遍历结束后，如果栈中没有左括号，说明我们将字符串 s 中的所有左括号闭合，返回 True，否则返回 False。

  注意到有效字符串的长度一定为偶数，因此如果字符串的长度为奇数，我们可以直接返回 False，省去后续的遍历判断过程。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public boolean isValid(String s) { int n = s.length(); if (n % 2 == 1) { return false; } Map<Character, Character> pairs = new HashMap<Character, Character>() {{ put(')', '('); put(']', '['); put('}', '{'); }}; Deque<Character> stack = new LinkedList<Character>(); for (int i = 0; i < n; i++) { char ch = s.charAt(i); if (pairs.containsKey(ch)) { if (stack.isEmpty() || stack.peek() != pairs.get(ch)) { return false; } stack.pop(); } else { stack.push(ch); } } return stack.isEmpty(); } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  func isValid(s string) bool { stack := []byte{} leftOk:=func(ch byte) bool{ return ch=='('||ch=='['||ch=='{' } check :=func(topc,c byte) bool { return (c==')'&&topc=='(')||(c==']'&&topc=='[')||(c=='}'&&topc=='{') } // 遇到左括号就压入栈中，遇到右括号就从栈顶取出括号是否配对，如果不配对就返回false，配对继续遍历 for i:=0;i<len(s);i++{ if leftOk(s[i]){ stack = append(stack,s[i]) }else{ if len(stack)!=0&&check(stack[len(stack)-1],s[i]){ stack = stack[:len(stack)-1] }else{ return false } } } // fmt.Println(string(stack)) return len(stack)==0 }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串 s 的长度。
  • 空间复杂度：O*(*n+∣Σ∣)，其中 Σ 表示字符集，本题中字符串只包含 66 种括号，∣Σ∣=6。栈中的字符数量为 O(n)，而哈希表使用的空间为 O(∣Σ∣)，相加即可得到总空间复杂度。

day15

225. 用队列实现栈

• 题目

  请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

  实现 MyStack 类：

  • void push(int x) 将元素 x 压入栈顶。
  • int pop() 移除并返回栈顶元素。
  • int top() 返回栈顶元素。
  • boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

  注意：

  • 你只能使用队列的基本操作 —— 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
  • 你所使用的语言也许不支持队列。 你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

  示例：

  1 2 3 4 5 6 7 8 9 10 11 12 13

  输入： ["MyStack", "push", "push", "top", "pop", "empty"] [[], [1], [2], [], [], []] 输出： [null, null, null, 2, 2, false] 解释： MyStack myStack = new MyStack(); myStack.push(1); myStack.push(2); myStack.top(); // 返回 2 myStack.pop(); // 返回 2 myStack.empty(); // 返回 False

  提示：

  • 1 <= x <= 9
  • 最多调用100 次 push、pop、top 和 empty
  • 每次调用 pop 和 top 都保证栈不为空

  **进阶：**你能否仅用一个队列来实现栈。

• 方法

  方法一：两个队列

  为了满足栈的特性，即最后入栈的元素最先出栈，在使用队列实现栈时，应满足队列前端的元素是最后入栈的元素。可以使用两个队列实现栈的操作，其中 queue1 用于存储栈内的元素，queue2 作为入栈操作的辅助队列。

  入栈操作时，首先将元素入队到 queue2，然后将 queue1 的全部元素依次出队并入队到 queue2，此时 queue2 的前端的元素即为新入栈的元素，再将 queue1 和 queue2 互换，则 queue1 的元素即为栈内的元素，queue1 的前端和后端分别对应栈顶和栈底。

  由于每次入栈操作都确保 queue1 的前端元素为栈顶元素，因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除 queue1 的前端元素并返回即可，获得栈顶元素操作只需要获得 queue1 的前端元素并返回即可（不移除元素）。

  由于 queue1 用于存储栈内的元素，判断栈是否为空时，只需要判断 queue1 是否为空即可。

  

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

  class MyStack { Queue<Integer> queue1; Queue<Integer> queue2; /** Initialize your data structure here. */ public MyStack() { queue1 = new LinkedList<Integer>(); queue2 = new LinkedList<Integer>(); } /** Push element x onto stack. */ public void push(int x) { queue2.offer(x); while (!queue1.isEmpty()) { queue2.offer(queue1.poll()); } Queue<Integer> temp = queue1; queue1 = queue2; queue2 = temp; } /** Removes the element on top of the stack and returns that element. */ public int pop() { return queue1.poll(); } /** Get the top element. */ public int top() { return queue1.peek(); } /** Returns whether the stack is empty. */ public boolean empty() { return queue1.isEmpty(); } }

  复杂度分析

  • 时间复杂度：入栈操作 O(n)，其余操作都是 O(1)，其中 n 是栈内的元素个数。 入栈操作需要将 queue1 中的 n 个元素出队，并入队 n+1 个元素到 queue2，共有 2n+1 次操作，每次出队和入队操作的时间复杂度都是 O(1)，因此入栈操作的时间复杂度是 O(n)。 出栈操作对应将 queue1 的前端元素出队，时间复杂度是 O(1)。 获得栈顶元素操作对应获得 queue1 的前端元素，时间复杂度是 O(1)。 判断栈是否为空操作只需要判断 queue1 是否为空，时间复杂度是 O(1)。
  • 空间复杂度：O(n)，其中 n 是栈内的元素个数。需要使用两个队列存储栈内的元素。

  方法二：一个队列

  方法一使用了两个队列实现栈的操作，也可以使用一个队列实现栈的操作。

  使用一个队列时，为了满足栈的特性，即最后入栈的元素最先出栈，同样需要满足队列前端的元素是最后入栈的元素。

  入栈操作时，首先获得入栈前的元素个数 n，然后将元素入队到队列，再将队列中的前 n 个元素（即除了新入栈的元素之外的全部元素）依次出队并入队到队列，此时队列的前端的元素即为新入栈的元素，且队列的前端和后端分别对应栈顶和栈底。

  由于每次入栈操作都确保队列的前端元素为栈顶元素，因此出栈操作和获得栈顶元素操作都可以简单实现。出栈操作只需要移除队列的前端元素并返回即可，获得栈顶元素操作只需要获得队列的前端元素并返回即可（不移除元素）。

  由于队列用于存储栈内的元素，判断栈是否为空时，只需要判断队列是否为空即可。

  

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  class MyStack { Queue<Integer> queue; /** Initialize your data structure here. */ public MyStack() { queue = new LinkedList<Integer>(); } /** Push element x onto stack. */ public void push(int x) { int n = queue.size(); queue.offer(x); for (int i = 0; i < n; i++) { queue.offer(queue.poll()); } } /** Removes the element on top of the stack and returns that element. */ public int pop() { return queue.poll(); } /** Get the top element. */ public int top() { return queue.peek(); } /** Returns whether the stack is empty. */ public boolean empty() { return queue.isEmpty(); } }

  复杂度分析

  • 时间复杂度：入栈操作 O(n)，其余操作都是 O(1)，其中 n 是栈内的元素个数。 入栈操作需要将队列中的 n 个元素出队，并入队 n+1 个元素到队列，共有 2n+1 次操作，每次出队和入队操作的时间复杂度都是 O(1)，因此入栈操作的时间复杂度是 O(n)。 出栈操作对应将队列的前端元素出队，时间复杂度是 O(1)。 获得栈顶元素操作对应获得队列的前端元素，时间复杂度是 O(1)。 判断栈是否为空操作只需要判断队列是否为空，时间复杂度是 O(1)。
  • 空间复杂度：O(n)，其中 n 是栈内的元素个数。需要使用一个队列存储栈内的元素。

day16

232. 用栈实现队列

• 题目

  请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）：

  实现 MyQueue 类：

  • void push(int x) 将元素 x 推到队列的末尾
  • int pop() 从队列的开头移除并返回元素
  • int peek() 返回队列开头的元素
  • boolean empty() 如果队列为空，返回 true ；否则，返回 false

  说明：

  • 你 只能 使用标准的栈操作 —— 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
  • 你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。

  示例 1：

  1 2 3 4 5 6 7 8 9 10 11 12 13

  输入： ["MyQueue", "push", "push", "peek", "pop", "empty"] [[], [1], [2], [], [], []] 输出： [null, null, null, 1, 1, false] 解释： MyQueue myQueue = new MyQueue(); myQueue.push(1); // queue is: [1] myQueue.push(2); // queue is: [1, 2] (leftmost is front of the queue) myQueue.peek(); // return 1 myQueue.pop(); // return 1, queue is [2] myQueue.empty(); // return false

  提示：

  • 1 <= x <= 9
  • 最多调用 100 次 push、pop、peek 和 empty
  • 假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）

  进阶：

  • 你能否实现每个操作均摊时间复杂度为 O(1) 的队列？换句话说，执行 n 个操作的总时间复杂度为 O(n) ，即使其中一个操作可能花费较长时间。

• 方法

  https://leetcode.cn/problems/implement-queue-using-stacks/solution/yong-zhan-shi-xian-dui-lie-by-leetcode/

• 代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  class MyQueue { Stack<Integer> s1; Stack<Integer> s2; public MyQueue() { this.s1=new Stack<>(); this.s2=new Stack<>(); } public void push(int x) { s1.push(x); } public int pop() { while(s1.size()!=0){ s2.push(s1.pop()); } int res=s2.pop(); while(s2.size()!=0){ s1.push(s2.pop()); } return res; } public int peek() { while(s1.size()!=0){ s2.push(s1.pop()); } int res=s2.peek(); while(s2.size()!=0){ s1.push(s2.pop()); } return res; } public boolean empty() { return s1.empty(); } }

day17

239. 滑动窗口最大值

• 题目

  给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

  返回 滑动窗口中的最大值 。

  示例 1：

  1 2 3 4 5 6 7 8 9 10 11

  输入：nums = [1,3,-1,-3,5,3,6,7], k = 3 输出：[3,3,5,5,6,7] 解释： 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 3 1 [3 -1 -3] 5 3 6 7 3 1 3 [-1 -3 5] 3 6 7 5 1 3 -1 [-3 5 3] 6 7 5 1 3 -1 -3 [5 3 6] 7 6 1 3 -1 -3 5 [3 6 7] 7

  示例 2：

  1 2	输入：nums = [1], k = 1 输出：[1]

  提示：

  • 1 <= nums.length <= 105
  • -104 <= nums[i] <= 104
  • 1 <= k <= nums.length

• 方法一（超时）

  暴力解法，依次移动窗口，不断寻找最大值，当然可以取巧：每一次只滑动一个索引位置，因此，每一次滑动窗口内的数已经知道了最大的数。如果最大的数还在下一次滑动窗口内，那么就可以利用这个属性，只需要比较上次滑动窗口的最大值和这次滑动窗口的末尾索引处的值，就可以得出下一次滑动窗口的最大值了，而不用傻乎乎的重复比较。当然，还是超时了…

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  class Solution { public int[] maxSlidingWindow(int[] nums, int k) { int len=nums.length; int max=Integer.MIN_VALUE; int index=-1; int[] arr = new int[len-k+1]; for(int i=0;i<len-k+1;i++){ if(index!=0){ if(max<nums[i+k-1]){ max=nums[i+k-1]; } } max=Integer.MIN_VALUE; index=-1; for(int j=i;j<i+k;j++){ if(max<nums[j]){ max=nums[j]; index=j; } } arr[i]=max; } return arr; } } /** 已经知道上一个最大的数了， 记录这个最大的数的位置如果不是窗口的第一位，显然具有利用价值： 无需比较上次窗口的最后一位，只需要比较窗口的下一位即可。 */

• 其他方法

  优先队列、单调队列（双端队列的特殊情况）

  https://leetcode.cn/problems/sliding-window-maximum/solution/hua-dong-chuang-kou-zui-da-zhi-by-leetco-ki6m/

day18

1047. 删除字符串中的所有相邻重复项

• 题目

  给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

  在 S 上反复执行重复项删除操作，直到无法继续删除。

  在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

  示例：

  1 2 3 4

  输入："abbaca" 输出："ca" 解释： 例如，在 "abbaca" 中，我们可以删除 "bb" 由于两字母相邻且相同，这是此时唯一可以执行删除操作的重复项。之后我们得到字符串 "aaca"，其中又只有 "aa" 可以执行重复项删除操作，所以最后的字符串为 "ca"。

  提示：

  1. 1 <= S.length <= 20000
  2. S 仅由小写英文字母组成。

• 解法

  方法一：栈

  充分理解题意后，我们可以发现，当字符串中同时有多组相邻重复项时，我们无论是先删除哪一个，都不会影响最终的结果。因此我们可以从左向右顺次处理该字符串。

  而消除一对相邻重复项可能会导致新的相邻重复项出现，如从字符串 abba 中删除 bb 会导致出现新的相邻重复项 aa 出现。因此我们需要保存当前还未被删除的字符。一种显而易见的数据结构呼之欲出：栈。我们只需要遍历该字符串，如果当前字符和栈顶字符相同，我们就贪心地将其消去，否则就将其入栈即可。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  class Solution { public String removeDuplicates(String s) { StringBuffer stack = new StringBuffer(); int top = -1; for (int i = 0; i < s.length(); ++i) { char ch = s.charAt(i); if (top >= 0 && stack.charAt(top) == ch) { stack.deleteCharAt(top); --top; } else { stack.append(ch); ++top; } } return stack.toString(); } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串的长度。我们只需要遍历该字符串一次。
  • 空间复杂度：O(n) 或 O(1))，取决于使用的语言提供的字符串类是否提供了类似「入栈」和「出栈」的接口。注意返回值不计入空间复杂度。

day19

151. 颠倒字符串中的单词

• 题目

  给你一个字符串 s ，颠倒字符串中 单词 的顺序。

  单词 是由非空格字符组成的字符串。s 中使用至少一个空格将字符串中的 单词 分隔开。

  返回 单词 顺序颠倒且 单词 之间用单个空格连接的结果字符串。

  **注意：**输入字符串 s中可能会存在前导空格、尾随空格或者单词间的多个空格。返回的结果字符串中，单词间应当仅用单个空格分隔，且不包含任何额外的空格。

  示例 1：

  1 2	输入：s = "the sky is blue" 输出："blue is sky the"

  示例 2：

  1 2 3

  输入：s = " hello world " 输出："world hello" 解释：颠倒后的字符串中不能存在前导空格和尾随空格。

  示例 3：

  1 2 3

  输入：s = "a good example" 输出："example good a" 解释：如果两个单词间有多余的空格，颠倒后的字符串需要将单词间的空格减少到仅有一个。

  提示：

  • 1 <= s.length <= 104
  • s 包含英文大小写字母、数字和空格 ' '
  • s 中 至少存在一个 单词

• 方法一

  思路：

  1. 去除首部空格
  2. 将空格之间的子串追加到字符串累加器并附带一个空格
  3. 追加完过后，再以空格分隔字符串
  4. 倒序数组，追加空格即可

  代码：（空间复杂度较高）

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  class Solution { public String reverseWords(String s) { char[] chs = s.toCharArray(); char prev = 0; StringBuilder stringBuilder = new StringBuilder(); int index=-1; for (int i = 0; i < s.length(); i++) { if (chs[i]!=' '){ index=i; break; } } for (int i = index; i < chs.length; i++) { if (chs[i] == ' ' && prev == ' ') {//如果当前字符和上一个字符为' ', continue; } stringBuilder.append(chs[i]); prev = chs[i]; } String str = stringBuilder.toString(); String[] split = str.split(" "); stringBuilder = new StringBuilder(); for (int i = split.length - 1; i > 0; i--) { stringBuilder.append(split[i]).append(' '); } stringBuilder.append(split[0]); return stringBuilder.toString(); } }

• 方法二

  https://leetcode.cn/problems/reverse-words-in-a-string/solution/fan-zhuan-zi-fu-chuan-li-de-dan-ci-by-leetcode-sol/

day20

541. 反转字符串 II

• 题目

  给定一个字符串 s 和一个整数 k，从字符串开头算起，每计数至 2k 个字符，就反转这 2k 字符中的前 k 个字符。

  • 如果剩余字符少于 k 个，则将剩余字符全部反转。
  • 如果剩余字符小于 2k 但大于或等于 k 个，则反转前 k 个字符，其余字符保持原样。

  示例 1：

  1 2	输入：s = "abcdefg", k = 2 输出："bacdfeg"

  示例 2：

  1 2	输入：s = "abcd", k = 2 输出："bacd"

  提示：

  • 1 <= s.length <= 104
  • s 仅由小写英文组成
  • 1 <= k <= 104

• 方法

  方法一：模拟

  我们直接按题意进行模拟：反转每个下标从 2k2k 的倍数开始的，长度为 kk 的子串。若该子串长度不足 kk，则反转整个子串。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class Solution { public String reverseStr(String s, int k) { int n = s.length(); char[] arr = s.toCharArray(); for (int i = 0; i < n; i += 2 * k) { reverse(arr, i, Math.min(i + k, n) - 1); } return new String(arr); } public void reverse(char[] arr, int left, int right) { while (left < right) { char temp = arr[left]; arr[left] = arr[right]; arr[right] = temp; left++; right--; } } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是字符串 s 的长度。
  • 空间复杂度：O(1) 或 O(n)，取决于使用的语言中字符串类型的性质。如果字符串是可修改的，那么我们可以直接在原字符串上修改，空间复杂度为 O(1)，否则需要使用 O(n) 的空间将字符串临时转换为可以修改的数据结构（例如数组），空间复杂度为 O(n)。

day21

1. 两数之和

• 题目

  给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

  你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

  你可以按任意顺序返回答案。

  示例 1：

  1 2 3

  输入：nums = [2,7,11,15], target = 9 输出：[0,1] 解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

  示例 2：

  1 2	输入：nums = [3,2,4], target = 6 输出：[1,2]

  示例 3：

  1 2	输入：nums = [3,3], target = 6 输出：[0,1]

  提示：

  • 2 <= nums.length <= 104
  • -109 <= nums[i] <= 109
  • -109 <= target <= 109
  • 只会存在一个有效答案

  **进阶：**你可以想出一个时间复杂度小于 O(n2) 的算法吗？

• 方法

  方法一：暴力枚举

  思路及算法

  最容易想到的方法是枚举数组中的每一个数 x，寻找数组中是否存在 target - x。当我们使用遍历整个数组的方式寻找 target - x 时，需要注意到每一个位于 x 之前的元素都已经和 x 匹配过，因此不需要再进行匹配。而每一个元素不能被使用两次，所以我们只需要在 x 后面的元素中寻找 target - x。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13

  class Solution { public int[] twoSum(int[] nums, int target) { int n = nums.length; for (int i = 0; i < n; ++i) { for (int j = i + 1; j < n; ++j) { if (nums[i] + nums[j] == target) { return new int[]{i, j}; } } } return new int[0]; } }

  复杂度分析

  • 时间复杂度：O(N^2^)，其中 N 是数组中的元素数量。最坏情况下数组中任意两个数都要被匹配一次。
  • 空间复杂度：O(1)。

  方法二：哈希表

  思路及算法

  此题，如果使用方法一，显然时间复杂度过高。结合题意：在一堆值里找一个值，应该考虑转化为hash的数据结构，hash的时间复杂度为O(1)

  注意到方法一的时间复杂度较高的原因是寻找 target - x 的时间复杂度过高。因此，我们需要一种更优秀的方法，能够快速寻找数组中是否存在目标元素。如果存在，我们需要找出它的索引。使用哈希表，可以将寻找 target - x 的时间复杂度降低到从 O(N) 降低到 O(1)。这样我们创建一个哈希表，对于每一个 x，我们首先查询哈希表中是否存在 target - x，然后将 x 插入到哈希表中，即可保证不会让 x 和自己匹配。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13

  class Solution { public int[] twoSum(int[] nums, int target) { Map<Integer, Integer> hashtable = new HashMap<Integer, Integer>(); for (int i = 0; i < nums.length; ++i) { // 将此处的n次循环变为1次即可得到结果，这就是hash的好处 if (hashtable.containsKey(target - nums[i])) { return new int[]{hashtable.get(target - nums[i]), i}; } hashtable.put(nums[i], i); } return new int[0]; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 是数组中的元素数量。对于每一个元素 x，我们可以 O(1) 地寻找 target - x。
  • 空间复杂度：O(N)，其中 N 是数组中的元素数量。主要为哈希表的开销。

day22

15. 三数之和

• 题目

  给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 *a，b，c ，*使得 a + b + c = 0 ？请你找出所有和为 0 且不重复的三元组。

  **注意：**答案中不可以包含重复的三元组。

  示例 1：

  1 2	输入：nums = [-1,0,1,2,-1,-4] 输出：[[-1,-1,2],[-1,0,1]]

  示例 2：

  1 2	输入：nums = [] 输出：[]

  示例 3：

  1 2	输入：nums = [0] 输出：[]

  提示：

  • 0 <= nums.length <= 3000
  • -105 <= nums[i] <= 105

• 解法

  方法一：排序 + 双指针

  题目中要求找到所有「不重复」且和为 0 的三元组，这个「不重复」的要求使得我们无法简单地使用三重循环枚举所有的三元组。这是因为在最坏的情况下，数组中的元素全部为 0，即

  1	[0, 0, 0, 0, 0, ..., 0, 0, 0]

  任意一个三元组的和都为 00。如果我直接使用三重循环枚举三元组，会得到 O(N^3^) 个满足题目要求的三元组（其中 N 是数组的长度）时间复杂度至少为 O(N^3^)。在这之后，我们还需要使用哈希表进行去重操作，得到不包含重复三元组的最终答案，又消耗了大量的空间。这个做法的时间复杂度和空间复杂度都很高，因此我们要换一种思路来考虑这个问题。

  「不重复」的本质是什么？我们保持三重循环的大框架不变，只需要保证：

  • 第二重循环枚举到的元素不小于当前第一重循环枚举到的元素；
  • 第三重循环枚举到的元素不小于当前第二重循环枚举到的元素。

  也就是说，我们枚举的三元组 (a, b, c) 满足 a≤b≤c，保证了只有 (a, b, c) 这个顺序会被枚举到，而 (b, a, c)、(c, b, a) 等等这些不会，这样就减少了重复。要实现这一点，我们可以将数组中的元素从小到大进行排序，随后使用普通的三重循环就可以满足上面的要求。

  同时，对于每一重循环而言，相邻两次枚举的元素不能相同，否则也会造成重复。举个例子，如果排完序的数组为

  1 2	[0, 1, 2, 2, 2, 3] ^ ^ ^

  我们使用三重循环枚举到的第一个三元组为 (0, 1, 2)，如果第三重循环继续枚举下一个元素，那么仍然是三元组 (0, 1, 2)，产生了重复。因此我们需要将第三重循环「跳到」下一个不相同的元素，即数组中的最后一个元素 3，枚举三元组 (0, 1, 3)。

  下面给出了改进的方法的伪代码实现：

  1 2 3 4 5 6 7 8 9 10

  nums.sort() for first = 0 .. n-1 // 只有和上一次枚举的元素不相同，我们才会进行枚举 if first == 0 or nums[first] != nums[first-1] then for second = first+1 .. n-1 if second == first+1 or nums[second] != nums[second-1] then for third = second+1 .. n-1 if third == second+1 or nums[third] != nums[third-1] then // 判断是否有 a+b+c==0 check(first, second, third)

  这种方法的时间复杂度仍然为 O(N^3^)，毕竟我们还是没有跳出三重循环的大框架。然而它是很容易继续优化的，可以发现，如果我们固定了前两重循环枚举到的元素 a 和 b，那么只有唯一的 c 满足 a+b+c=0。当第二重循环往后枚举一个元素 b’ 时，由于 b’ > b，那么满足 a+b’+c’=0 的 c’ 一定有 c’ < c，即 c’ 在数组中一定出现在 c 的左侧。也就是说，我们可以从小到大枚举 b，同时从大到小枚举 c，即第二重循环和第三重循环实际上是并列的关系。

  有了这样的发现，我们就可以保持第二重循环不变，而将第三重循环变成一个从数组最右端开始向左移动的指针，从而得到下面的伪代码：

  1 2 3 4 5 6 7 8 9 10 11 12

  nums.sort() for first = 0 .. n-1 if first == 0 or nums[first] != nums[first-1] then // 第三重循环对应的指针 third = n-1 for second = first+1 .. n-1 if second == first+1 or nums[second] != nums[second-1] then // 向左移动指针，直到 a+b+c 不大于 0 while nums[first]+nums[second]+nums[third] > 0 third = third-1 // 判断是否有 a+b+c==0 check(first, second, third)

  这个方法就是我们常说的「双指针」，当我们需要枚举数组中的两个元素时，如果我们发现随着第一个元素的递增，第二个元素是递减的，那么就可以使用双指针的方法，将枚举的时间复杂度从 O(N^2)O(N2) 减少至 O(N)。为什么是 O(N) 呢？这是因为在枚举的过程每一步中，「左指针」会向右移动一个位置（也就是题目中的 b），而「右指针」会向左移动若干个位置，这个与数组的元素有关，但我们知道它一共会移动的位置数为 O(N)，均摊下来，每次也向左移动一个位置，因此时间复杂度为 O(N)。

  注意到我们的伪代码中还有第一重循环，时间复杂度为 O(N)O(N)，因此枚举的总时间复杂度为 O(N^2^)。由于排序的时间复杂度为 O(NlogN)，在渐进意义下小于前者，因此算法的总时间复杂度为 O(N^2^)。

  上述的伪代码中还有一些细节需要补充，例如我们需要保持左指针一直在右指针的左侧（即满足 b≤c），具体可以参考下面的代码，均给出了详细的注释。

  代码：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41

  class Solution { public List<List<Integer>> threeSum(int[] nums) { int n = nums.length; Arrays.sort(nums); List<List<Integer>> ans = new ArrayList<List<Integer>>(); // 枚举 a for (int first = 0; first < n; ++first) { // 需要和上一次枚举的数不相同 if (first > 0 && nums[first] == nums[first - 1]) { continue; } // c 对应的指针初始指向数组的最右端 int third = n - 1; int target = -nums[first]; // 枚举 b for (int second = first + 1; second < n; ++second) { // 需要和上一次枚举的数不相同 if (second > first + 1 && nums[second] == nums[second - 1]) { continue; } // 需要保证 b 的指针在 c 的指针的左侧 while (second < third && nums[second] + nums[third] > target) { --third; } // 如果指针重合，随着 b 后续的增加 // 就不会有满足 a+b+c=0 并且 b<c 的 c 了，可以退出循环 if (second == third) { break; } if (nums[second] + nums[third] == target) { List<Integer> list = new ArrayList<Integer>(); list.add(nums[first]); list.add(nums[second]); list.add(nums[third]); ans.add(list); } } } return ans; } }

  复杂度分析

  • 时间复杂度：O(N^2^)，其中 N 是数组 nums 的长度。
  • 空间复杂度：O(logN)。我们忽略存储答案的空间，额外的排序的空间复杂度为 O(logN)。然而我们修改了输入的数组 nums，在实际情况下不一定允许，因此也可以看成使用了一个额外的数组存储了 nums 的副本并进行排序，空间复杂度为 O(N)。

day23

202. 快乐数

• 题目

  编写一个算法来判断一个数 n 是不是快乐数。

  「快乐数」 定义为：

  • 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
  • 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
  • 如果这个过程 结果为 1，那么这个数就是快乐数。

  如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

  示例 1：

  1 2 3 4 5 6 7

  输入：n = 19 输出：true 解释： 12 + 92 = 82 82 + 22 = 68 62 + 82 = 100 12 + 02 + 02 = 1

  示例 2：

  1 2	输入：n = 2 输出：false

  提示：

  • 1 <= n <= 231 - 1

• 解法

  暴力错误且超时

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public boolean isHappy(int n) { int tmp=n; while(true){ tmp=get(tmp); if(tmp==n) return false; else if(tmp==1) return true; } } public int get(int n) { int tmp=n; int sum=0; int r=0; while(tmp!=0){ r = tmp%10; sum = r*r+sum; tmp = tmp/10; } return sum; } }

  超时的原因在于：条件判断错误，不是一定要出现到初始数字才会陷入死循环，有可能是中途的某个节点出现循环，例如：数字116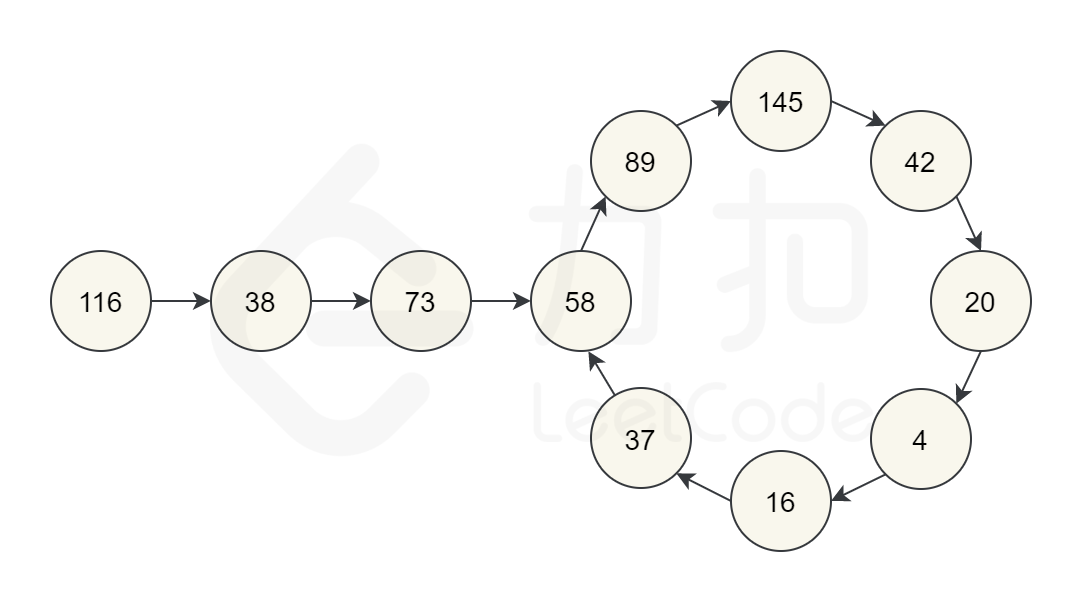

  

  显然，需要使用弗洛伊德判圈算法（龟兔赛跑算法）–> 快慢指针法：一个快指针和一个慢指针同时出发，如果快指针追上了慢指针说明是一个死循环，就返回false

  快慢指针法

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { public boolean isHappy(int n) { int slowRunner = n; int fastRunner = getNext(n); while (fastRunner != 1 && slowRunner != fastRunner) { slowRunner = getNext(slowRunner); fastRunner = getNext(getNext(fastRunner)); } return fastRunner == 1; } public int getNext(int n) { int tmp=n; int sum=0; int r=0; while(tmp!=0){ r = tmp%10; sum = r*r+sum; tmp = tmp/10; } return sum; } }

day24

454. 四数相加 II

• 题目

  给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：

  • 0 <= i, j, k, l < n
  • nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0

  示例 1：

  1 2 3 4 5 6

  输入：nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2] 输出：2 解释： 两个元组如下： 1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0 2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0

  示例 2：

  1 2	输入：nums1 = [0], nums2 = [0], nums3 = [0], nums4 = [0] 输出：1

  提示：

  • n == nums1.length
  • n == nums2.length
  • n == nums3.length
  • n == nums4.length
  • 1 <= n <= 200
  • -228 <= nums1[i], nums2[i], nums3[i], nums4[i] <= 228

• 解法：分组+hash表

  思路与算法

  我们可以将四个数组分成两部分，A 和 B 为一组，C 和 D 为另外一组。

  对于 A 和 B，我们使用二重循环对它们进行遍历，得到所有 A[i]+B[j] 的值并存入哈希映射中。对于哈希映射中的每个键值对，每个键表示一种 A[i]+B[j]，对应的值为 A[i]+B[j] 出现的次数。

  对于 CC 和 DD，我们同样使用二重循环对它们进行遍历。当遍历到 C[k]+D[l] 时，如果 -(C[k]+D[l]) 出现在哈希映射中，那么将 -(C[k]+D[l]) 对应的值累加进答案中。

  最终即可得到满足 A[i]+B[j]+C[k]+D[l]=0 的四元组数目。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  class Solution { public int fourSumCount(int[] A, int[] B, int[] C, int[] D) { Map<Integer, Integer> countAB = new HashMap<Integer, Integer>(); for (int u : A) { for (int v : B) { countAB.put(u + v, countAB.getOrDefault(u + v, 0) + 1); } } int ans = 0; for (int u : C) { for (int v : D) { if (countAB.containsKey(-u - v)) { ans += countAB.get(-u - v); } } } return ans; } }

  复杂度分析

  • 时间复杂度：O(n^2^)。我们使用了两次二重循环，时间复杂度均为 O(n^2^)。在循环中对哈希映射进行的修改以及查询操作的期望时间复杂度均为 O(1)，因此总时间复杂度为 O(n^2^)。
  • 空间复杂度：O(n^2^)，即为哈希映射需要使用的空间。在最坏的情况下，A[i]+B[j] 的值均不相同，因此值的个数为 n^2^，也就需要 O(n^2^) 的空间。

day25

100. 相同的树

• 题目

  给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

  如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

  示例 1：

  

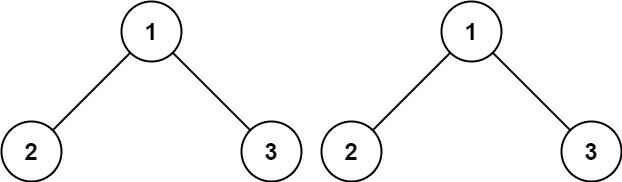
  1 2	输入：p = [1,2,3], q = [1,2,3] 输出：true

  示例 2：

  

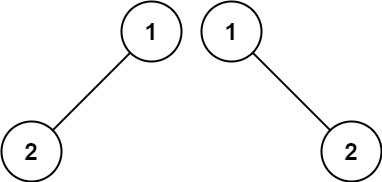
  1 2	输入：p = [1,2], q = [1,null,2] 输出：false

  示例 3：

  

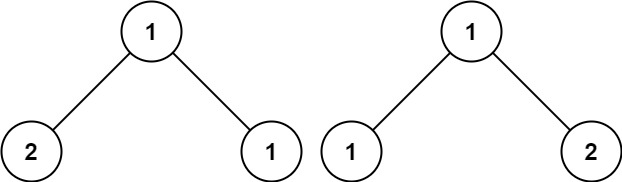
  1 2	输入：p = [1,2,1], q = [1,1,2] 输出：false

  提示：

  • 两棵树上的节点数目都在范围 [0, 100] 内
  • -104 <= Node.val <= 104

• 解法

  两个二叉树相同，当且仅当两个二叉树的结构完全相同，且所有对应节点的值相同。因此，可以通过搜索的方式判断两个二叉树是否相同。

  方法一：深度优先搜索

  如果两个二叉树都为空，则两个二叉树相同。如果两个二叉树中有且只有一个为空，则两个二叉树一定不相同。

  如果两个二叉树都不为空，那么首先判断它们的根节点的值是否相同，若不相同则两个二叉树一定不同，若相同，再分别判断两个二叉树的左子树是否相同以及右子树是否相同。这是一个递归的过程，因此可以使用深度优先搜索，递归地判断两个二叉树是否相同。

  1 2 3 4 5 6 7 8 9 10 11 12 13

  class Solution { public boolean isSameTree(TreeNode p, TreeNode q) { if (p == null && q == null) { return true; } else if (p == null || q == null) { return false; } else if (p.val != q.val) { return false; } else { return isSameTree(p.left, q.left) && isSameTree(p.right, q.right); } } }

  复杂度分析

  • 时间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会访问到该节点，因此被访问到的节点数不会超过较小的二叉树的节点数。
  • 空间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点数。空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数。

  方法二：广度优先搜索

  也可以通过广度优先搜索判断两个二叉树是否相同。同样首先判断两个二叉树是否为空，如果两个二叉树都不为空，则从两个二叉树的根节点开始广度优先搜索。

  使用两个队列分别存储两个二叉树的节点。初始时将两个二叉树的根节点分别加入两个队列。每次从两个队列各取出一个节点，进行如下比较操作。

  1. 比较两个节点的值，如果两个节点的值不相同则两个二叉树一定不同；
  2. 如果两个节点的值相同，则判断两个节点的子节点是否为空，如果只有一个节点的左子节点为空，或者只有一个节点的右子节点为空，则两个二叉树的结构不同，因此两个二叉树一定不同；
  3. 如果两个节点的子节点的结构相同，则将两个节点的非空子节点分别加入两个队列，子节点加入队列时需要注意顺序，如果左右子节点都不为空，则先加入左子节点，后加入右子节点。

  如果搜索结束时两个队列同时为空，则两个二叉树相同。如果只有一个队列为空，则两个二叉树的结构不同，因此两个二叉树不同。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

  class Solution { public boolean isSameTree(TreeNode p, TreeNode q) { if (p == null && q == null) { return true; } else if (p == null || q == null) { return false; } Queue<TreeNode> queue1 = new LinkedList<TreeNode>(); Queue<TreeNode> queue2 = new LinkedList<TreeNode>(); queue1.offer(p); queue2.offer(q); while (!queue1.isEmpty() && !queue2.isEmpty()) { TreeNode node1 = queue1.poll(); TreeNode node2 = queue2.poll(); if (node1.val != node2.val) { return false; } TreeNode left1 = node1.left, right1 = node1.right, left2 = node2.left, right2 = node2.right; if (left1 == null ^ left2 == null) { return false; } if (right1 == null ^ right2 == null) { return false; } if (left1 != null) { queue1.offer(left1); } if (right1 != null) { queue1.offer(right1); } if (left2 != null) { queue2.offer(left2); } if (right2 != null) { queue2.offer(right2); } } return queue1.isEmpty() && queue2.isEmpty(); } }

  复杂度分析

  • 时间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点数。对两个二叉树同时进行广度优先搜索，只有当两个二叉树中的对应节点都不为空时才会访问到该节点，因此被访问到的节点数不会超过较小的二叉树的节点数。
  • 空间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点数。空间复杂度取决于队列中的元素个数，队列中的元素个数不会超过较小的二叉树的节点数。

day26

101. 对称二叉树

• 题目

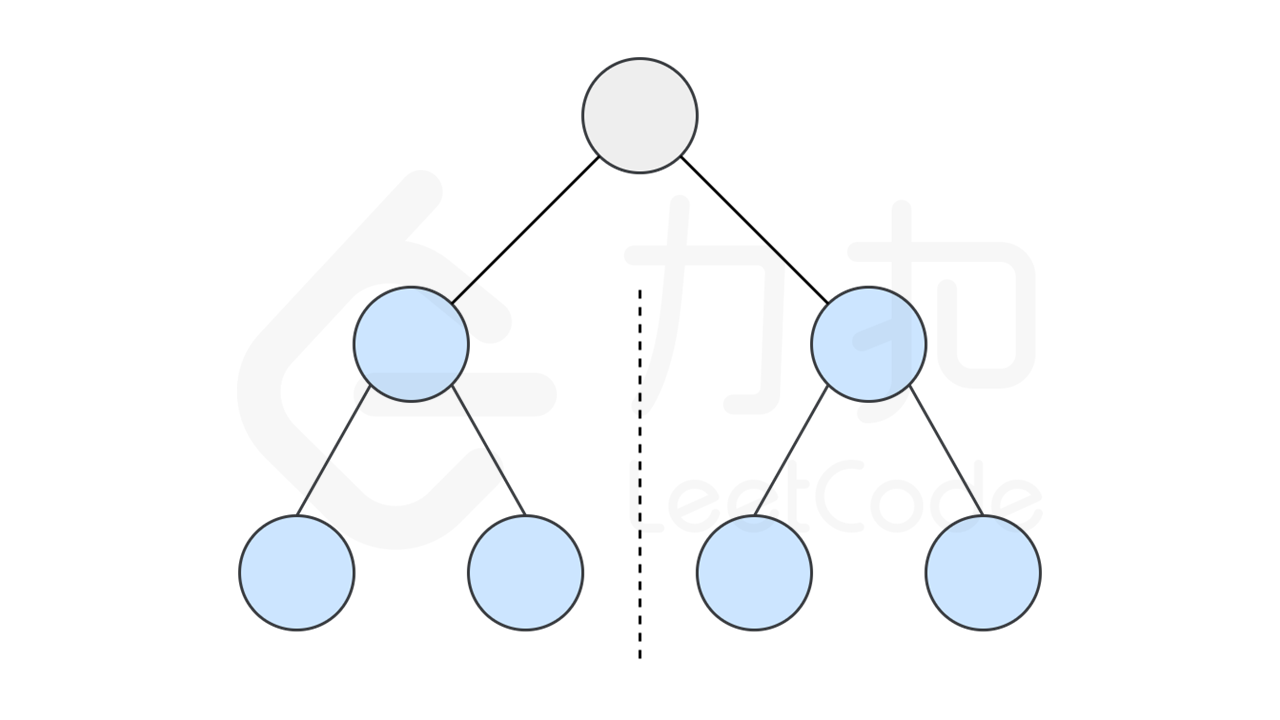
  给你一个二叉树的根节点 root ， 检查它是否轴对称。

  示例 1：

  

  1 2	输入：root = [1,2,2,3,4,4,3] 输出：true

  示例 2：

  

  1 2	输入：root = [1,2,2,null,3,null,3] 输出：false

  提示：

  • 树中节点数目在范围 [1, 1000] 内
  • -100 <= Node.val <= 100

  **进阶：**你可以运用递归和迭代两种方法解决这个问题吗？

• 解法

  方法一：递归

  思路和算法

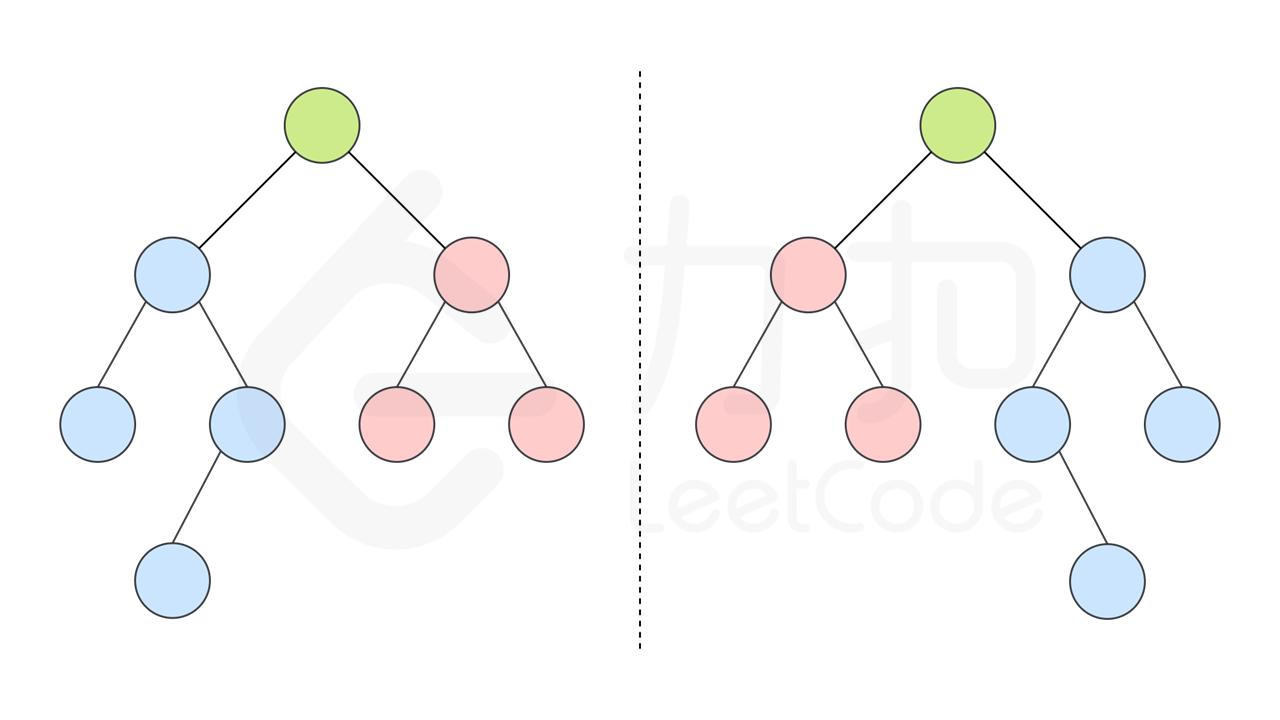
  如果一个树的左子树与右子树镜像对称，那么这个树是对称的。

  

  因此，该问题可以转化为：两个树在什么情况下互为镜像？

  如果同时满足下面的条件，两个树互为镜像：

  • 它们的两个根结点具有相同的值
  • 每个树的右子树都与另一个树的左子树镜像对称

  

  我们可以实现这样一个递归函数，通过「同步移动」两个指针的方法来遍历这棵树，p 指针和 q 指针一开始都指向这棵树的根，随后 p 右移时，q 左移，p 左移时，q 右移。每次检查当前 p 和 q 节点的值是否相等，如果相等再判断左右子树是否对称。

  代码如下：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public boolean isSymmetric(TreeNode root) { return check(root.left, root.right); } public boolean check(TreeNode p, TreeNode q) { if (p == null && q == null) { return true; }else if (p == null || q == null) { return false; }else if (p.val != q.val ){ return false; } return check(p.left, q.right) && check(p.right, q.left); // 就是看左子树和右子树节点是否相同 } }

  复杂度分析

  假设树上一共 n 个节点。

  • 时间复杂度：这里遍历了这棵树，渐进时间复杂度为 O(n)。
  • 空间复杂度：这里的空间复杂度和递归使用的栈空间有关，这里递归层数不超过 n，故渐进空间复杂度为 O(n)。

  方法二：迭代

  思路和算法

  「方法一」中我们用递归的方法实现了对称性的判断，那么如何用迭代的方法实现呢？首先我们引入一个队列，这是把递归程序改写成迭代程序的常用方法。初始化时我们把根节点入队两次。每次提取两个结点并比较它们的值（队列中每两个连续的结点应该是相等的，而且它们的子树互为镜像），然后将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时，或者我们检测到树不对称（即从队列中取出两个不相等的连续结点）时，该算法结束。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public boolean isSymmetric(TreeNode root) { return check(root, root); } public boolean check(TreeNode u, TreeNode v) { Queue<TreeNode> q = new LinkedList<TreeNode>(); q.offer(u); q.offer(v); while (!q.isEmpty()) { u = q.poll(); v = q.poll(); if (u == null && v == null) { continue; } if ((u == null || v == null) || (u.val != v.val)) { return false; } // 核心代码 q.offer(u.left); q.offer(v.right); q.offer(u.right); q.offer(v.left); } return true; } }

  复杂度分析

  • 时间复杂度：O(n)，同「方法一」。
  • 空间复杂度：这里需要用一个队列来维护节点，每个节点最多进队一次，出队一次，队列中最多不会超过 n 个点，故渐进空间复杂度为 O(n)。

day27

104. 二叉树的最大深度

• 题目

  给定一个二叉树，找出其最大深度。

  二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

  说明: 叶子节点是指没有子节点的节点。

  示例： 给定二叉树 [3,9,20,null,null,15,7]，

  1 2 3 4 5

  3 / \ 9 20 / \ 15 7

  返回它的最大深度 3 。

• 解法

  方法一：深度优先搜索

  思路与算法

  如果我们知道了左子树和右子树的最大深度 l 和 r，那么该二叉树的最大深度即为max(l,r)+1

  而左子树和右子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法来计算二叉树的最大深度。具体而言，在计算当前二叉树的最大深度时，可以先递归计算出其左子树和右子树的最大深度，然后在 O(1) 时间内计算出当前二叉树的最大深度。递归在访问到空节点时退出。

  1 2 3 4 5 6 7 8 9 10 11

  class Solution { public int maxDepth(TreeNode root) { if (root == null) { return 0; } else { int leftHeight = maxDepth(root.left); int rightHeight = maxDepth(root.right); return Math.max(leftHeight, rightHeight) + 1; } } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉树节点的个数。每个节点在递归中只被遍历一次。
  • 空间复杂度：O(height)，其中 height 表示二叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于二叉树的高度。

  方法二：广度优先搜索

  思路与算法

  我们也可以用「广度优先搜索」的方法来解决这道题目，但我们需要对其进行一些修改，此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候，不同于广度优先搜索的每次只从队列里拿出一个节点，我们需要将队列里的所有节点都拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展，最后我们用一个变量 ans 来维护拓展的次数，该二叉树的最大深度即为 ans。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  class Solution { public int maxDepth(TreeNode root) { if (root == null) { return 0; } Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.offer(root); int ans = 0; while (!queue.isEmpty()) { int size = queue.size(); while (size > 0) { TreeNode node = queue.poll(); if (node.left != null) { queue.offer(node.left); } if (node.right != null) { queue.offer(node.right); } size--; } ans++; } return ans; } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  /** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func maxDepth(root *TreeNode) int { if root==nil { return 0 } depth:=0 queue:=[]*TreeNode{root} for len(queue)!=0{ n:=len(queue) for i:=0;i<n;i++{ node:=queue[i] // fmt.Println(node.Val) if node.Left!=nil{ queue=append(queue,node.Left) } if node.Right!=nil{ queue=append(queue,node.Right) } } queue=queue[n:] depth++ } return depth }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉树的节点个数。与方法一同样的分析，每个节点只会被访问一次。
  • 空间复杂度：此方法空间的消耗取决于队列存储的元素数量，其在最坏情况下会达到 O(n)。

day28

111. 二叉树的最小深度

• 题目

  给定一个二叉树，找出其最小深度。

  最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

  **说明：**叶子节点是指没有子节点的节点。

  示例 1：

  

  1 2	输入：root = [3,9,20,null,null,15,7] 输出：2

  示例 2：

  1 2	输入：root = [2,null,3,null,4,null,5,null,6] 输出：5

  提示：

  • 树中节点数的范围在 [0, 105] 内
  • -1000 <= Node.val <= 1000

• 解法

  方法一：深度优先搜索

  思路及解法

  首先可以想到使用深度优先搜索的方法，遍历整棵树，记录最小深度。

  对于每一个非叶子节点，我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题，可以递归地解决该问题。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public int minDepth(TreeNode root) { if (root==null) return 0; int l=Integer.MAX_VALUE; int r=Integer.MAX_VALUE; if (root.left==null&&root.right==null) return 1; if (root.left!=null){ l=minDepth(root.left)+1; } if(root.right!=null){ // System.out.println(root.val); r=minDepth(root.right)+1; } return l>r?r:l; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。
  • 空间复杂度：O(H)，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(log N)。

  方法二：广度优先搜索

  思路及解法

  同样，我们可以想到使用广度优先搜索的方法，遍历整棵树。

  当我们找到一个叶子节点时，直接返回这个叶子节点的深度。广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public int minDepth(TreeNode root) { if (root==null) return 0; if (root.left==null&&root.right==null) return 1; int layerNum=1; Queue<TreeNode> queue=new LinkedList<>(); queue.offer(root); while(!queue.isEmpty()){ int size = queue.size(); while(size>0){ TreeNode node = queue.poll(); if(node.left==null&&node.right==null) return layerNum; if(node.left!=null) queue.offer(node.left); if(node.right!=null) queue.offer(node.right); size--; } layerNum++; } return layerNum; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。
  • 空间复杂度：O(N)，其中 N 是树的节点数。空间复杂度主要取决于队列的开销，队列中的元素个数不会超过树的节点数。

day29

112. 路径总和

• 题目

  给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

  叶子节点 是指没有子节点的节点。

  示例 1：

  

  1 2 3

  输入：root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出：true 解释：等于目标和的根节点到叶节点路径如上图所示。

  示例 2：

  

  1 2 3 4 5 6

  输入：root = [1,2,3], targetSum = 5 输出：false 解释：树中存在两条根节点到叶子节点的路径： (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。

  示例 3：

  1 2 3

  输入：root = [], targetSum = 0 输出：false 解释：由于树是空的，所以不存在根节点到叶子节点的路径。

  提示：

  • 树中节点的数目在范围 [0, 5000] 内
  • -1000 <= Node.val <= 1000
  • -1000 <= targetSum <= 1000

• 解法

  写在前面

  注意到本题的要求是，询问是否有从「根节点」到某个「叶子节点」经过的路径上的节点之和等于目标和。核心思想是对树进行一次遍历，在遍历时记录从根节点到当前节点的路径和，以防止重复计算。

  需要特别注意的是，给定的 root 可能为空。

  方法一：广度优先搜索

  思路及算法

  首先我们可以想到使用广度优先搜索的方式，记录从根节点到当前节点的路径和，以防止重复计算。

  这样我们使用两个队列，分别存储将要遍历的节点，以及根节点到这些节点的路径和即可。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { public boolean hasPathSum(TreeNode root, int sum) { if (root == null) { return false; } Queue<TreeNode> queNode = new LinkedList<>(); Queue<Integer> queVal = new LinkedList<>(); queNode.offer(root); queVal.offer(root.val); while (!queNode.isEmpty()) { TreeNode now = queNode.poll(); int temp = queVal.poll(); if (now.left == null && now.right == null) { if (temp == sum) { return true; } continue; } if (now.left != null) { queNode.offer(now.left); queVal.offer(now.left.val + temp); } if (now.right != null) { queNode.offer(now.right); queVal.offer(now.right.val + temp); } } return false; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。
  • 空间复杂度：O(N)，其中 N 是树的节点数。空间复杂度主要取决于队列的开销，队列中的元素个数不会超过树的节点数。

  方法二：递归

  思路及算法

  观察要求我们完成的函数，我们可以归纳出它的功能：询问是否存在从当前节点 root 到叶子节点的路径，满足其路径和为 sum。

  假定从根节点到当前节点的值之和为 val，我们可以将这个大问题转化为一个小问题：是否存在从当前节点的子节点到叶子的路径，满足其路径和为 sum - val。

  不难发现这满足递归的性质，若当前节点就是叶子节点，那么我们直接判断 sum 是否等于 val 即可（因为路径和已经确定，就是当前节点的值，我们只需要判断该路径和是否满足条件）。若当前节点不是叶子节点，我们只需要递归地询问它的子节点是否能满足条件即可。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  class Solution { public boolean hasPathSum(TreeNode root, int sum) { if (root == null) { return false; } if (root.left == null && root.right == null) { return sum == root.val; } return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val); } } // 或者：正向思维，遍历二叉树，将到达叶子节点的路径和累加与 targetSum 比较，如果相等就返回true class Solution { public boolean hasPathSum(TreeNode root, int targetSum) { return doSome(root,targetSum,0); } public boolean doSome(TreeNode root,int targetSum,int tmp){ if (root==null) return false; // 叶子节点 if(root.left==null&&root.right==null) { if(tmp+root.val==targetSum){ return true; } else { tmp=0; return false; } } if(root.left!=null) { boolean l =doSome(root.left,targetSum,tmp+root.val); if (l) return true; } if(root.right!=null) { boolean r = doSome(root.right,targetSum,tmp+root.val); if (r) return true; } return false; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 是树的节点数。对每个节点访问一次。
  • 空间复杂度：O(H)，其中 H 是树的高度。空间复杂度主要取决于递归时栈空间的开销，最坏情况下，树呈现链状，空间复杂度为 O(N)。平均情况下树的高度与节点数的对数正相关，空间复杂度为 O(log N)。

day30

222. 完全二叉树的节点个数

• 题目

  给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

  完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。

  示例 1：

  

  1 2	输入：root = [1,2,3,4,5,6] 输出：6

  示例 2：

  1 2	输入：root = [] 输出：0

  示例 3：

  1 2	输入：root = [1] 输出：1

  提示：

  • 树中节点的数目范围是[0, 5 * 104]
  • 0 <= Node.val <= 5 * 104
  • 题目数据保证输入的树是 完全二叉树

  **进阶：**遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗？

• 解法

  方法一：深度优先遍历

  1 2 3 4 5 6 7 8 9 10 11 12

  class Solution { public int countNodes(TreeNode root) { if(root == null) { return 0; } int left = countNodes(root.left); int right = countNodes(root.right); return left+right+1; } }

  方法二：广度优先遍历

  一如既往，广度优先貌似硬是要比深度优先慢一些

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class Solution { public int countNodes(TreeNode root) { if (root==null) return 0; Queue<TreeNode> queue=new LinkedList<>(); int count=0; queue.offer(root); while(!queue.isEmpty()){ int size = queue.size(); while(size>0){ TreeNode n = queue.poll(); if (n!=null) count++; if (n.left!=null) queue.offer(n.left); if (n.right!=null) queue.offer(n.right); size--; } } return count; } }

  方法三：二分查找 + 位运算

  对于任意二叉树，都可以通过广度优先搜索或深度优先搜索计算节点个数，时间复杂度和空间复杂度都是 O(n)，其中 n 是二叉树的节点个数。这道题规定了给出的是完全二叉树，因此可以利用完全二叉树的特性计算节点个数。

  规定根节点位于第 0 层，完全二叉树的最大层数为 h。根据完全二叉树的特性可知，完全二叉树的最左边的节点一定位于最底层，因此从根节点出发，每次访问左子节点，直到遇到叶子节点，该叶子节点即为完全二叉树的最左边的节点，经过的路径长度即为最大层数 h。

  当 0≤i<h 时，第 i 层包含 2^i^ 个节点，最底层包含的节点数最少为 1，最多为 2^h^。

  当最底层包含 1 个节点时，完全二叉树的节点个数是 $$ \sum_{i=0}^{h-1}2^i+1=2^h $$ 当最底层包含 2^h^ 个节点时，完全二叉树的节点个数是 $$ \sum_{i=0}^{h}2^i=2^{h+1}-1 $$ 因此对于最大层数为 h 的完全二叉树，节点个数一定在 [2^h^,2^h+1^-1] 的范围内，可以在该范围内通过二分查找的方式得到完全二叉树的节点个数。

  具体做法是，根据节点个数范围的上下界得到当前需要判断的节点个数 k，如果第 k 个节点存在，则节点个数一定大于或等于 k，如果第 k 个节点不存在，则节点个数一定小于 k，由此可以将查找的范围缩小一半，直到得到节点个数。

  如何判断第 k 个节点是否存在呢？如果第 k 个节点位于第 h 层，则 k 的二进制表示包含 h+1 位，其中最高位是 1，其余各位从高到低表示从根节点到第 k 个节点的路径，0 表示移动到左子节点，1 表示移动到右子节点。通过位运算得到第 k 个节点对应的路径，判断该路径对应的节点是否存在，即可判断第 k 个节点是否存在。

  

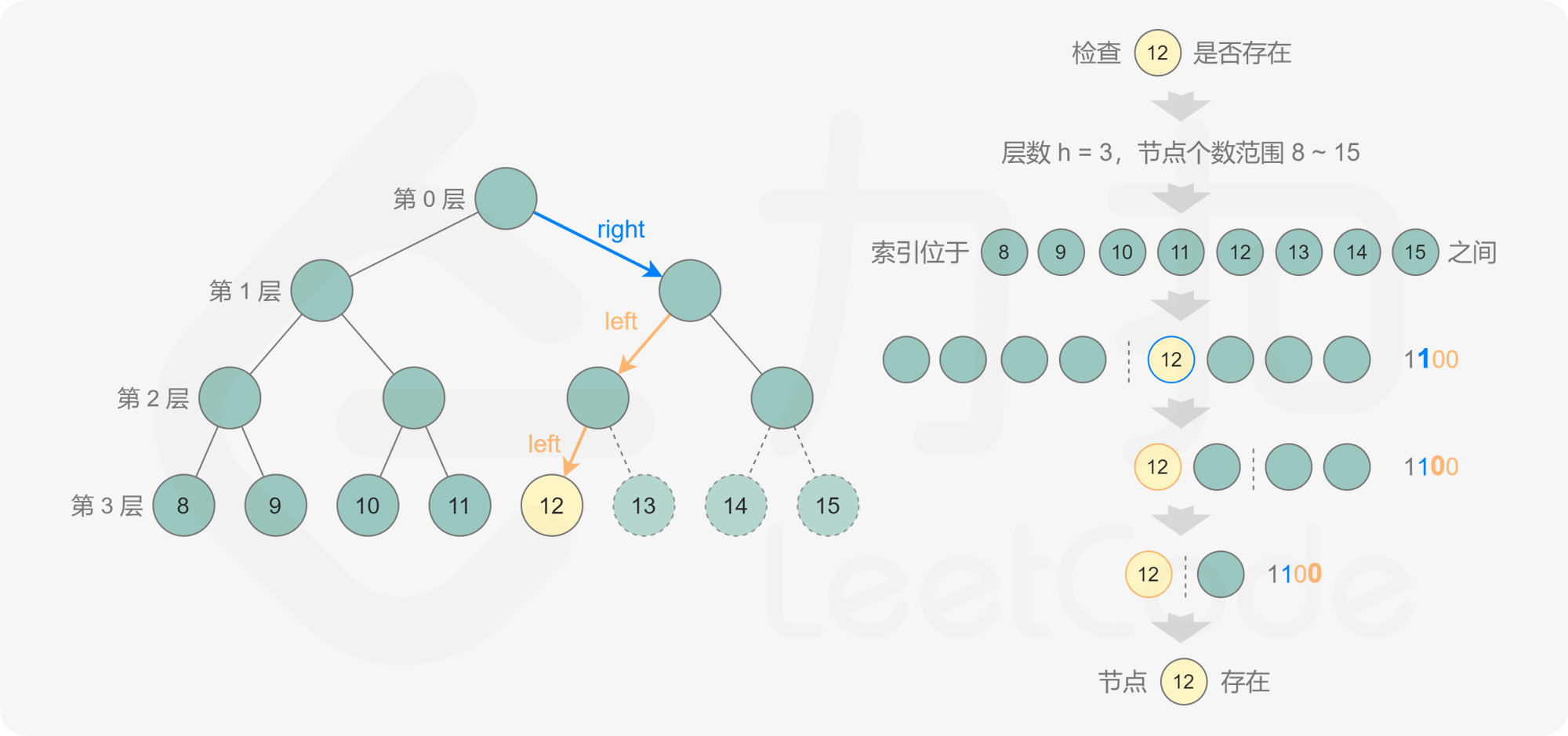
  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

  class Solution { public int countNodes(TreeNode root) { if (root == null) { return 0; } int level = 0; TreeNode node = root; while (node.left != null) { level++; node = node.left; } int low = 1 << level, high = (1 << (level + 1)) - 1; while (low < high) { int mid = (high - low + 1) / 2 + low; if (exists(root, level, mid)) { low = mid; } else { high = mid - 1; } } return low; } public boolean exists(TreeNode root, int level, int k) { int bits = 1 << (level - 1); TreeNode node = root; while (node != null && bits > 0) { if ((bits & k) == 0) { node = node.left; } else { node = node.right; } bits >>= 1; } return node != null; } }

  复杂度分析

  • 时间复杂度：O(log^2^n)，其中 n 是完全二叉树的节点数。 首先需要 O(h) 的时间得到完全二叉树的最大层数，其中 h 是完全二叉树的最大层数。 使用二分查找确定节点个数时，需要查找的次数为 O(log 2^h^)=O(h)，每次查找需要遍历从根节点开始的一条长度为 h 的路径，需要 O(h) 的时间，因此二分查找的总时间复杂度是 O(h^2^)。 因此总时间复杂度是 O(h^2^)。由于完全二叉树满足 2^h^≤n<2^h+1^，因此有 O(h)=O(log n)，O(h^2^)=O(log^2^ n)。
  • 空间复杂度：O(1)。只需要维护有限的额外空间。

day31

226. 翻转二叉树

• 题目

  给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

  示例 1：

  

  1 2	输入：root = [4,2,7,1,3,6,9] 输出：[4,7,2,9,6,3,1]

  示例 2：

  

  1 2	输入：root = [2,1,3] 输出：[2,3,1]

  示例 3：

  1 2	输入：root = [] 输出：[]

  提示：

  • 树中节点数目范围在 [0, 100] 内
  • -100 <= Node.val <= 100

• 解法

  方法一：深度优先遍历

  思路与算法

  这是一道很经典的二叉树问题。显然，我们从根节点开始，递归地对树进行遍历，并从叶子节点先开始翻转。如果当前遍历到的节点 root 的左右两棵子树都已经翻转，那么我们只需要交换两棵子树的位置，即可完成以 root 为根节点的整棵子树的翻转。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public TreeNode invertTree(TreeNode root) { if(root==null) return null; // 先交换一下左右子树 TreeNode tmp = root.right; root.right = root.left; root.left = tmp; // 此时已经交换过子树了，所以分别遍历左右子树 root.left = invertTree(root.left); root.right = invertTree(root.right); return root; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 为二叉树节点的数目。我们会遍历二叉树中的每一个节点，对每个节点而言，我们在常数时间内交换其两棵子树。
  • 空间复杂度：O(N)。使用的空间由递归栈的深度决定，它等于当前节点在二叉树中的高度。在平均情况下，二叉树的高度与节点个数为对数关系，即 O*(logN)。而在最坏情况下，树形成链状，空间复杂度为 O(N)。

  方法二：广度优先遍历

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  public TreeNode invertTree(TreeNode root) { if (root == null) return root; Queue<TreeNode> queue = new LinkedList<>(); queue.add(root);//相当于把数据加入到队列尾部 while (!queue.isEmpty()) { //poll方法相当于移除队列头部的元素 TreeNode node = queue.poll(); //先交换子节点 TreeNode left = node.left; node.left = node.right; node.right = left; if (node.left != null) queue.add(node.left); if (node.right != null) queue.add(node.right); } return root; }

day32

236. 二叉树的最近公共祖先

• 题目

  给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

  百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

  示例 1：

  

  1 2 3

  输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出：3 解释：节点 5 和节点 1 的最近公共祖先是节点 3 。

  示例 2：

  

  1 2 3

  输入：root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出：5 解释：节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。

  示例 3：

  1 2	输入：root = [1,2], p = 1, q = 2 输出：1

  提示：

  • 树中节点数目在范围 [2, 105] 内。
  • -109 <= Node.val <= 109
  • 所有 Node.val 互不相同 。
  • p != q
  • p 和 q 均存在于给定的二叉树中。

• 解法

  方法零：两层递归

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if (root==null) return null; //左子树是否含有这两个节点，如果有，就继续递归，直到左子树不再同时含有两个节点 if (doSome(root.left,p)&&doSome(root.left,q)) { return lowestCommonAncestor(root.left,p,q); } if (doSome(root.right,p)&&doSome(root.right,q)){ return lowestCommonAncestor(root.right,p,q); } return root; } // 检查 node子树里是否含有n节点 public boolean doSome(TreeNode node,TreeNode n){ if (node==null)return false; if (node.val==n.val){ return true; } boolean l = doSome(node.left,n); boolean r = doSome(node.right,n); return l||r; } }

  方法一：递归

  思路和算法

  我们递归遍历整棵二叉树，定义 f~x~ 表示 x 节点的子树中是否包含 p 节点或 q 节点，如果包含为 true，否则为 false。那么符合条件的最近公共祖先 x 一定满足如下条件：(f^lson^ && f^rson^) ∣∣ ((x = p ∣∣ x = q) && (f^lson^ ∣∣ f^rson^))

  其中 lson 和 rson 分别代表 x 节点的左孩子和右孩子。初看可能会感觉条件判断有点复杂，我们来一条条看，f^lson^ && f^rson^` 说明左子树和右子树均包含 p 节点或 q 节点，如果左子树包含的是 p 节点，那么右子树只能包含 q 节点，反之亦然，因为 p 节点和 q 节点都是不同且唯一的节点，因此如果满足这个判断条件即可说明 x 就是我们要找的最近公共祖先。再来看第二条判断条件，这个判断条件即是考虑了 x 恰好是 p 节点或 q 节点且它的左子树或右子树有一个包含了另一个节点的情况，因此如果满足这个判断条件亦可说明 x 就是我们要找的最近公共祖先。

  你可能会疑惑这样找出来的公共祖先深度是否是最大的。其实是最大的，因为我们是自底向上从叶子节点开始更新的，所以在所有满足条件的公共祖先中一定是深度最大的祖先先被访问到，且由于 f~x~ 本身的定义很巧妙，在找到最近公共祖先 x 以后，f~x~ 按定义被设置为 true ，即假定了这个子树中只有一个 p 节点或 q 节点，因此其他公共祖先不会再被判断为符合条件。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { private TreeNode ans; public Solution() { this.ans = null; } private boolean dfs(TreeNode root, TreeNode p, TreeNode q) { if (root == null) return false; boolean lson = dfs(root.left, p, q); boolean rson = dfs(root.right, p, q); if ((lson && rson) || ((root.val == p.val || root.val == q.val) && (lson || rson))) { ans = root; } return lson || rson || (root.val == p.val || root.val == q.val); } public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { this.dfs(root, p, q); return this.ans; } }

  复杂度分析

  • 时间复杂度：O(N) ，其中 N 是二叉树的节点数。二叉树的所有节点有且只会被访问一次，因此时间复杂度为 O(N)。
  • 空间复杂度：O(N) ，其中 N 是二叉树的节点数。递归调用的栈深度取决于二叉树的高度，二叉树最坏情况下为一条链，此时高度为 N ，因此空间复杂度为 O(N)。

  方法二：存储父节点

  思路

  我们可以用哈希表存储所有节点的父节点，然后我们就可以利用节点的父节点信息从 p 结点开始不断往上跳，并记录已经访问过的节点，再从 q 节点开始不断往上跳，如果碰到已经访问过的节点，那么这个节点就是我们要找的最近公共祖先。

  算法

  1. 从根节点开始遍历整棵二叉树，用哈希表记录每个节点的父节点指针。
  2. 从 p 节点开始不断往它的祖先移动，并用数据结构记录已经访问过的祖先节点。
  3. 同样，我们再从 q 节点开始不断往它的祖先移动，如果有祖先已经被访问过，即意味着这是 p 和 q 的深度最深的公共祖先，即 LCA 节点。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { Map<Integer, TreeNode> parent = new HashMap<Integer, TreeNode>(); Set<Integer> visited = new HashSet<Integer>(); public void dfs(TreeNode root) { if (root.left != null) { parent.put(root.left.val, root); dfs(root.left); } if (root.right != null) { parent.put(root.right.val, root); dfs(root.right); } } public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { dfs(root); while (p != null) { visited.add(p.val); p = parent.get(p.val); } while (q != null) { if (visited.contains(q.val)) { return q; } q = parent.get(q.val); } return null; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 是二叉树的节点数。二叉树的所有节点有且只会被访问一次，从 p 和 q 节点往上跳经过的祖先节点个数不会超过 N，因此总的时间复杂度为 O(N)。
  • 空间复杂度：O(N) ，其中 N 是二叉树的节点数。递归调用的栈深度取决于二叉树的高度，二叉树最坏情况下为一条链，此时高度为 N，因此空间复杂度为 O(N)，哈希表存储每个节点的父节点也需要 O(N) 的空间复杂度，因此最后总的空间复杂度为 O(N)。

day33

257. 二叉树的所有路径

• 题目

  给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

  叶子节点 是指没有子节点的节点。

  示例 1：

  

  1 2	输入：root = [1,2,3,null,5] 输出：["1->2->5","1->3"]

  示例 2：

  1 2	输入：root = [1] 输出：["1"]

  提示：

  • 树中节点的数目在范围 [1, 100] 内
  • -100 <= Node.val <= 100

• 解法

  方法一：深度优先搜索

  思路与算法

  最直观的方法是使用深度优先搜索。在深度优先搜索遍历二叉树时，我们需要考虑当前的节点以及它的孩子节点。

  • 如果当前节点不是叶子节点，则在当前的路径末尾添加该节点，并继续递归遍历该节点的每一个孩子节点。
  • 如果当前节点是叶子节点，则在当前路径末尾添加该节点后我们就得到了一条从根节点到叶子节点的路径，将该路径加入到答案即可。

  如此，当遍历完整棵二叉树以后我们就得到了所有从根节点到叶子节点的路径。当然，深度优先搜索也可以使用非递归的方式实现，这里不再赘述。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public List<String> binaryTreePaths(TreeNode root) { List<String> paths = new ArrayList<String>(); constructPaths(root, "", paths); return paths; } public void constructPaths(TreeNode root, String path, List<String> paths) { if (root != null) { StringBuffer pathSB = new StringBuffer(path); pathSB.append(Integer.toString(root.val)); if (root.left == null && root.right == null) { // 当前节点是叶子节点 paths.add(pathSB.toString()); // 把路径加入到答案中 } else { pathSB.append("->"); // 当前节点不是叶子节点，继续递归遍历 constructPaths(root.left, pathSB.toString(), paths); constructPaths(root.right, pathSB.toString(), paths); } } } }

  复杂度分析

  • 时间复杂度：O(N^2^)，其中 N 表示节点数目。在深度优先搜索中每个节点会被访问一次且只会被访问一次，每一次会对 path 变量进行拷贝构造，时间代价为 O(N) ，故时间复杂度为 O(N^2^)。

  • 空间复杂度：O(N^2^)，其中 N 表示节点数目。除答案数组外我们需要考虑递归调用的栈空间。在最坏情况下，当二叉树中每个节点只有一个孩子节点时，即整棵二叉树呈一个链状，此时递归的层数为 N，此时每一层的 path 变量的空间代价的总和为 $$ O(\sum_{i = 1}^{N} i) = O(N^2) $$ 空间复杂度为 O(N^2^)。最好情况下，当二叉树为平衡二叉树时，它的高度为 log N ，此时空间复杂度为 $$ O((\log {N})^2) $$ 。

  方法二：广度优先搜索

  思路与算法

  我们也可以用广度优先搜索来实现。我们维护一个队列，存储节点以及根到该节点的路径。一开始这个队列里只有根节点。在每一步迭代中，我们取出队列中的首节点，如果它是叶子节点，则将它对应的路径加入到答案中。如果它不是叶子节点，则将它的所有孩子节点加入到队列的末尾。当队列为空时广度优先搜索结束，我们即能得到答案。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  class Solution { public List<String> binaryTreePaths(TreeNode root) { List<String> paths = new ArrayList<String>(); if (root == null) { return paths; } Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>(); Queue<String> pathQueue = new LinkedList<String>(); nodeQueue.offer(root); pathQueue.offer(Integer.toString(root.val)); while (!nodeQueue.isEmpty()) { TreeNode node = nodeQueue.poll(); String path = pathQueue.poll(); if (node.left == null && node.right == null) { paths.add(path); } else { if (node.left != null) { nodeQueue.offer(node.left); pathQueue.offer(new StringBuffer(path).append("->").append(node.left.val).toString()); } if (node.right != null) { nodeQueue.offer(node.right); pathQueue.offer(new StringBuffer(path).append("->").append(node.right.val).toString()); } } } return paths; } }

  复杂度分析

  • 时间复杂度：O(N^2^)，其中 N 表示节点数目。分析同方法一。
  • 空间复杂度：O(N^2^)，其中 N 表示节点数目。在最坏情况下，队列中会存在 N 个节点，保存字符串的队列中每个节点的最大长度为 N，故空间复杂度为 O(N^2^)。

day34

404. 左叶子之和

• 题目

  给定二叉树的根节点 root ，返回所有左叶子之和。

  示例 1：

  

  1 2 3

  输入: root = [3,9,20,null,null,15,7] 输出: 24 解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

  示例 2:

  1 2	输入: root = [1] 输出: 0

  提示:

  • 节点数在 [1, 1000] 范围内
  • -1000 <= Node.val <= 1000

• 解法

  一个节点为「左叶子」节点，当且仅当它是某个节点的左子节点，并且它是一个叶子结点。因此我们可以考虑对整棵树进行遍历，当我们遍历到节点 node 时，如果它的左子节点是一个叶子结点，那么就将它的左子节点的值累加计入答案。

  遍历整棵树的方法有深度优先搜索和广度优先搜索，下面分别给出了实现代码。

  方法一：深度优先搜索

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class Solution { public int sumOfLeftLeaves(TreeNode root) { return root != null ? dfs(root) : 0; } public int dfs(TreeNode node) { int ans = 0; if (node.left != null) { ans += isLeafNode(node.left) ? node.left.val : dfs(node.left); } if (node.right != null && !isLeafNode(node.right)) { ans += dfs(node.right); } return ans; } public boolean isLeafNode(TreeNode node) { return node.left == null && node.right == null; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是树中的节点个数。
  • 空间复杂度：O(n)。空间复杂度与深度优先搜索使用的栈的最大深度相关。在最坏的情况下，树呈现链式结构，深度为 O(n)，对应的空间复杂度也为 O(n)。

  方法二：广度优先搜索

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  class Solution { public int sumOfLeftLeaves(TreeNode root) { if (root == null) { return 0; } Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.offer(root); int ans = 0; while (!queue.isEmpty()) { TreeNode node = queue.poll(); if (node.left != null) { if (isLeafNode(node.left)) { ans += node.left.val; } else { queue.offer(node.left); } } if (node.right != null) { if (!isLeafNode(node.right)) { queue.offer(node.right); } } } return ans; } public boolean isLeafNode(TreeNode node) { return node.left == null && node.right == null; } }

  复杂度分析

  • 时间复杂度：O(n) ，其中 n 是树中的节点个数。
  • 空间复杂度：O(n) 。空间复杂度与广度优先搜索使用的队列需要的容量相关，为 O(n)。

day35

513. 找树左下角的值

• 题目

  给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

  假设二叉树中至少有一个节点。

  示例 1:

  

  1 2	输入: root = [2,1,3] 输出: 1

  示例 2:

  

  1 2	输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7

  提示:

  • 二叉树的节点个数的范围是 [1,104]
  • -231 <= Node.val <= 231 - 1

• 解法

  方法一：深度优先搜索

  使用 height 记录遍历到的节点的高度，curVal 记录高度在 curHeight 的最左节点的值。在深度优先搜索时，我们先搜索当前节点的左子节点，再搜索当前节点的右子节点，然后判断当前节点的高度 height 是否大于 curHeight，如果是，那么将 curVal 设置为当前结点的值,curHeight 设置为 height。

  因为我们先遍历左子树，然后再遍历右子树，所以对同一高度的所有节点，最左节点肯定是最先被遍历到的。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  class Solution { int curVal = 0; int curHeight = 0; public int findBottomLeftValue(TreeNode root) { int curHeight = 0; dfs(root, 0); return curVal; } public void dfs(TreeNode root, int height) { if (root == null) { return; } height++; dfs(root.left, height); dfs(root.right, height); // 相当于后续遍历麻，最先遍历的一定是左子节点，然后是右、根子节点 if (height > curHeight) { curHeight = height; curVal = root.val; } } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点数目。需要遍历 n 个节点。
  • 空间复杂度：O(n)。递归栈需要占用 O(n) 的空间。

  方法二：广度优先搜索

  使用广度优先搜索遍历每一层的节点。在遍历一个节点时，需要先把它的非空右子节点放入队列，然后再把它的非空左子节点放入队列，这样才能保证从右到左遍历每一层的节点。广度优先搜索所遍历的最后一个节点的值就是最底层最左边节点的值。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public int findBottomLeftValue(TreeNode root) { int ret = 0; Queue<TreeNode> queue = new ArrayDeque<TreeNode>(); queue.offer(root); while (!queue.isEmpty()) { TreeNode p = queue.poll(); if (p.right != null) { queue.offer(p.right); } if (p.left != null) { queue.offer(p.left); } ret = p.val; } return ret; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点数目。
  • 空间复杂度：O(n)。如果二叉树是满完全二叉树，那么队列 q 最多保存 2/n 个节点。

day36

559. N 叉树的最大深度

• 题目

  给定一个 N 叉树，找到其最大深度。

  最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

  N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

  示例 1：

  

  1 2	输入：root = [1,null,3,2,4,null,5,6] 输出：3

  示例 2：

  

  1 2	输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出：5

  提示：

  • 树的深度不会超过 1000 。
  • 树的节点数目位于 [0, 104] 之间。

• 解法

  方法一：深度优先搜索

  如果根节点有 N 个子节点，则这 N 个子节点对应 N 个子树。记 N 个子树的最大深度中的最大值为 maxChildDepth，则该 N 叉树的最大深度为 maxChildDepth+1。

  每个子树的最大深度又可以以同样的方式进行计算。因此我们可以用「深度优先搜索」的方法计算 N 叉树的最大深度。具体而言，在计算当前 N 叉树的最大深度时，可以先递归计算出其每个子树的最大深度，然后在 O(1) 的时间内计算出当前 N 叉树的最大深度。递归在访问到空节点时退出。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  class Solution { public int maxDepth(Node root) { if (root == null) { return 0; } int maxChildDepth = 0; List<Node> children = root.children; for (Node child : children) { int childDepth = maxDepth(child); maxChildDepth = Math.max(maxChildDepth, childDepth); } return maxChildDepth + 1; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为 N 叉树节点的个数。每个节点在递归中只被遍历一次。
  • 空间复杂度：O(height)，其中 height 表示 N 叉树的高度。递归函数需要栈空间，而栈空间取决于递归的深度，因此空间复杂度等价于 N 叉树的高度。

  方法二：广度优先搜索

  我们也可以用「广度优先搜索」的方法来解决这道题目，但我们需要对其进行一些修改，此时我们广度优先搜索的队列里存放的是「当前层的所有节点」。每次拓展下一层的时候，不同于广度优先搜索的每次只从队列里拿出一个节点，我们需要将队列里的所有节点都拿出来进行拓展，这样能保证每次拓展完的时候队列里存放的是当前层的所有节点，即我们是一层一层地进行拓展。最后我们用一个变量 ans 来维护拓展的次数，该 N 叉树的最大深度即为 ans。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { public int maxDepth(Node root) { if (root == null) { return 0; } Queue<Node> queue = new LinkedList<Node>(); queue.offer(root); int ans = 0; while (!queue.isEmpty()) { int size = queue.size(); while (size > 0) { Node node = queue.poll(); List<Node> children = node.children; for (Node child : children) { queue.offer(child); } size--; } ans++; } return ans; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为 N 叉树的节点个数。与方法一同样的分析，每个节点只会被访问一次。
  • 空间复杂度：此方法空间的消耗取决于队列存储的元素数量，其在最坏情况下会达到 O(n)。

day37

617. 合并二叉树

• 题目

  给你两棵二叉树： root1 和 root2 。

  想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

  返回合并后的二叉树。

  注意: 合并过程必须从两个树的根节点开始。

  示例 1：

  

  1 2	输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7] 输出：[3,4,5,5,4,null,7]

  示例 2：

  1 2	输入：root1 = [1], root2 = [1,2] 输出：[2,2]

  提示：

  • 两棵树中的节点数目在范围 [0, 2000] 内
  • -104 <= Node.val <= 104

• 解法

  方法一：深度优先搜索

  可以使用深度优先搜索合并两个二叉树。从根节点开始同时遍历两个二叉树，并将对应的节点进行合并。

  两个二叉树的对应节点可能存在以下三种情况，对于每种情况使用不同的合并方式。

  • 如果两个二叉树的对应节点都为空，则合并后的二叉树的对应节点也为空；
  • 如果两个二叉树的对应节点只有一个为空，则合并后的二叉树的对应节点为其中的非空节点；
  • 如果两个二叉树的对应节点都不为空，则合并后的二叉树的对应节点的值为两个二叉树的对应节点的值之和，此时需要显性合并两个节点。

  对一个节点进行合并之后，还要对该节点的左右子树分别进行合并。这是一个递归的过程。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public TreeNode mergeTrees(TreeNode root1, TreeNode root2) { TreeNode node; // 定义一个局部变量用于递归时，本层节点记录 if(root1==null&&root2==null){// 当两个根节点都是null，直接返回null return null; }else if(root1==null){// 当两个根节点有一个为空时，也直接返回非空节点，没必要加 return root2; }else if(root2==null){// 当两个根节点有一个为空时，也直接返回非空节点，没必要加 return root1; }else{// 当两个根节点都不为空的时候，先记录合并后的根节点 node = new TreeNode(root1.val+root2.val); } // 然后再递归的遍历左右子树 TreeNode left = mergeTrees(root1.left,root2.left); TreeNode right = mergeTrees(root1.right,root2.right); // 将左右子树的结果挂在新的根节点上 node.left = left; node.right = right; return node; } }

  复杂度分析

  • 时间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会对该节点进行显性合并操作，因此被访问到的节点数不会超过较小的二叉树的节点数。
  • 空间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数。

  方法二：广度优先搜索

  也可以使用广度优先搜索合并两个二叉树。首先判断两个二叉树是否为空，如果两个二叉树都为空，则合并后的二叉树也为空，如果只有一个二叉树为空，则合并后的二叉树为另一个非空的二叉树。

  如果两个二叉树都不为空，则首先计算合并后的根节点的值，然后从合并后的二叉树与两个原始二叉树的根节点开始广度优先搜索，从根节点开始同时遍历每个二叉树，并将对应的节点进行合并。

  使用三个队列分别存储合并后的二叉树的节点以及两个原始二叉树的节点。初始时将每个二叉树的根节点分别加入相应的队列。每次从每个队列中取出一个节点，判断两个原始二叉树的节点的左右子节点是否为空。如果两个原始二叉树的当前节点中至少有一个节点的左子节点不为空，则合并后的二叉树的对应节点的左子节点也不为空。对于右子节点同理。

  如果合并后的二叉树的左子节点不为空，则需要根据两个原始二叉树的左子节点计算合并后的二叉树的左子节点以及整个左子树。考虑以下两种情况：

  • 如果两个原始二叉树的左子节点都不为空，则合并后的二叉树的左子节点的值为两个原始二叉树的左子节点的值之和，在创建合并后的二叉树的左子节点之后，将每个二叉树中的左子节点都加入相应的队列；
  • 如果两个原始二叉树的左子节点有一个为空，即有一个原始二叉树的左子树为空，则合并后的二叉树的左子树即为另一个原始二叉树的左子树，此时也不需要对非空左子树继续遍历，因此不需要将左子节点加入队列。

  对于右子节点和右子树，处理方法与左子节点和左子树相同。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

  class Solution { public TreeNode mergeTrees(TreeNode t1, TreeNode t2) { if (t1 == null) { return t2; } if (t2 == null) { return t1; } TreeNode merged = new TreeNode(t1.val + t2.val); Queue<TreeNode> queue = new LinkedList<TreeNode>(); Queue<TreeNode> queue1 = new LinkedList<TreeNode>(); Queue<TreeNode> queue2 = new LinkedList<TreeNode>(); queue.offer(merged); queue1.offer(t1); queue2.offer(t2); while (!queue1.isEmpty() && !queue2.isEmpty()) { TreeNode node = queue.poll(), node1 = queue1.poll(), node2 = queue2.poll(); TreeNode left1 = node1.left, left2 = node2.left, right1 = node1.right, right2 = node2.right; if (left1 != null || left2 != null) { if (left1 != null && left2 != null) { TreeNode left = new TreeNode(left1.val + left2.val); node.left = left; queue.offer(left); queue1.offer(left1); queue2.offer(left2); } else if (left1 != null) { node.left = left1; } else if (left2 != null) { node.left = left2; } } if (right1 != null || right2 != null) { if (right1 != null && right2 != null) { TreeNode right = new TreeNode(right1.val + right2.val); node.right = right; queue.offer(right); queue1.offer(right1); queue2.offer(right2); } else if (right1 != null) { node.right = right1; } else { node.right = right2; } } } return merged; } }

  复杂度分析

  • 时间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。对两个二叉树同时进行广度优先搜索，只有当两个二叉树中的对应节点都不为空时才会访问到该节点，因此被访问到的节点数不会超过较小的二叉树的节点数。
  • 空间复杂度：O(min(m,n))，其中 m 和 n 分别是两个二叉树的节点个数。空间复杂度取决于队列中的元素个数，队列中的元素个数不会超过较小的二叉树的节点数。

day38

654. 最大二叉树

• 题目

  给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

  1. 创建一个根节点，其值为 nums 中的最大值。
  2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
  3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。

  返回 nums 构建的 *最大二叉树* 。

  示例 1：

  

  1 2 3 4 5 6 7 8 9 10 11 12

  输入：nums = [3,2,1,6,0,5] 输出：[6,3,5,null,2,0,null,null,1] 解释：递归调用如下所示： - [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。 - [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。 - 空数组，无子节点。 - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。 - 空数组，无子节点。 - 只有一个元素，所以子节点是一个值为 1 的节点。 - [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。 - 只有一个元素，所以子节点是一个值为 0 的节点。 - 空数组，无子节点。

  示例 2：

  

  1 2	输入：nums = [3,2,1] 输出：[3,null,2,null,1]

  提示：

  • 1 <= nums.length <= 1000
  • 0 <= nums[i] <= 1000
  • nums 中的所有整数 互不相同

• 解法

  方法一：递归

  思路与算法

  最简单的方法是直接按照题目描述进行模拟。

  我们用递归函数 construct(nums,left,right) 表示对数组 nums 中从 nums 到 的元素构建一棵树。我们首先找到这一区间中的最大值，记为 nums 中从 nums[best]，这样就确定了根节点的值。随后我们就可以进行递归：

  • 左子树为 construct(nums, left, best-1)；
  • 右子树为 construct(nums,best+1,right)。

  当递归到一个无效的区间（即 left*>*right）时，便可以返回一棵空的树。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public TreeNode constructMaximumBinaryTree(int[] nums) { return construct(nums, 0, nums.length - 1); } public TreeNode construct(int[] nums, int left, int right) { if (left > right) { return null; } int best = left; for (int i = left + 1; i <= right; ++i) { if (nums[i] > nums[best]) { best = i; } } TreeNode node = new TreeNode(nums[best]); node.left = construct(nums, left, best - 1); node.right = construct(nums, best + 1, right); return node; } }

  复杂度分析

  • 时间复杂度：O(n^2^)，其中 n 是数组 nums 的长度。在最坏的情况下，数组严格递增或递减，需要递归 n 层，第 i (0≤i<n) 层需要遍历 n-i 个元素以找出最大值，总时间复杂度为 O(n^2^)。
  • 空间复杂度：O(n)，即为最坏情况下需要使用的栈空间。

  方法二：单调栈

  思路与算法

  我们可以将题目中构造树的过程等价转换为下面的构造过程：

  • 初始时，我们只有一个根节点，其中存储了整个数组；
  • 在每一步操作中，我们可以「任选」一个存储了超过一个数的节点，找出其中的最大值并存储在该节点。最大值左侧的数组部分下放到该节点的左子节点，右侧的数组部分下放到该节点的右子节点；
  • 如果所有的节点都恰好存储了一个数，那么构造结束。

  由于最终构造出的是一棵树，因此无需按照题目的要求「递归」地进行构造，而是每次可以「任选」一个节点进行构造。这里可以类比一棵树的「深度优先搜索」和「广度优先搜索」，二者都可以起到遍历整棵树的效果。

  既然可以任意进行选择，那么我们不妨每次选择数组中最大值最大的那个节点进行构造。这样一来，我们就可以保证按照数组中元素降序排序的顺序依次构造每个节点。因此：

  当我们选择的节点中数组的最大值为 nums[i] 时，所有大于 nums[i] 的元素已经被构造过（即被单独放入某一个节点中），所有小于 nums[i] 的元素还没有被构造过。

  这就说明：

  在最终构造出的树上，以 nums[i] 为根节点的子树，在原数组中对应的区间，左边界为 nums[i] 左侧第一个比它大的元素所在的位置，右边界为 nums[i] 右侧第一个比它大的元素所在的位置。左右边界均为开边界。

  如果某一侧边界不存在，则那一侧边界为数组的边界。如果两侧边界均不存在，说明其为最大值，即根节点。

  并且：

  nums[i] 的父结点是两个边界中较小的那个元素对应的节点。

  因此，我们的任务变为：找出每一个元素左侧和右侧第一个比它大的元素所在的位置。这就是一个经典的单调栈问题了，可以参考 503. 下一个更大元素 II。如果左侧的元素较小，那么该元素就是左侧元素的右子节点；如果右侧的元素较小，那么该元素就是右侧元素的左子节点。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  class Solution { public TreeNode constructMaximumBinaryTree(int[] nums) { int n = nums.length; Deque<Integer> stack = new ArrayDeque<Integer>(); int[] left = new int[n]; int[] right = new int[n]; Arrays.fill(left, -1); Arrays.fill(right, -1); TreeNode[] tree = new TreeNode[n]; for (int i = 0; i < n; ++i) { tree[i] = new TreeNode(nums[i]); while (!stack.isEmpty() && nums[i] > nums[stack.peek()]) { right[stack.pop()] = i; } if (!stack.isEmpty()) { left[i] = stack.peek(); } stack.push(i); } TreeNode root = null; for (int i = 0; i < n; ++i) { if (left[i] == -1 && right[i] == -1) { root = tree[i]; } else if (right[i] == -1 || (left[i] != -1 && nums[left[i]] < nums[right[i]])) { tree[left[i]].right = tree[i]; } else { tree[right[i]].left = tree[i]; } } return root; } }

  我们还可以把最后构造树的过程放进单调栈求解的步骤中，省去用来存储左右边界的数组。下面的代码理解起来较为困难，同一个节点的左右子树会被多次赋值，读者可以仔细品味其妙处所在。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  class Solution { public TreeNode constructMaximumBinaryTree(int[] nums) { int n = nums.length; List<Integer> stack = new ArrayList<Integer>(); TreeNode[] tree = new TreeNode[n]; for (int i = 0; i < n; ++i) { tree[i] = new TreeNode(nums[i]); while (!stack.isEmpty() && nums[i] > nums[stack.get(stack.size() - 1)]) { tree[i].left = tree[stack.get(stack.size() - 1)]; stack.remove(stack.size() - 1); } if (!stack.isEmpty()) { tree[stack.get(stack.size() - 1)].right = tree[i]; } stack.add(i); } return tree[stack.get(0)]; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组 nums 的长度。单调栈求解左右边界和构造树均需要 O(n) 的时间。
  • 空间复杂度：O(n)，即为单调栈和数组 tree 需要使用的空间。

day39

144. 二叉树的前序遍历

• 题目

  给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

  示例 1：

  

  1 2	输入：root = [1,null,2,3] 输出：[1,2,3]

  示例 2：

  1 2	输入：root = [] 输出：[]

  示例 3：

  1 2	输入：root = [1] 输出：[1]

  示例 4：

  

  1 2	输入：root = [1,2] 输出：[1,2]

  示例 5：

  

  1 2	输入：root = [1,null,2] 输出：[1,2]

  提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

  **进阶：**递归算法很简单，你可以通过迭代算法完成吗？

• 解法

  方法一：递归

  思路与算法

  首先我们需要了解什么是二叉树的前序遍历：按照访问根节点——左子树——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。

  定义 preorder(root) 表示当前遍历到 root 节点的答案。按照定义，我们只要首先将 root 节点的值加入答案，然后递归调用 preorder(root.left) 来遍历 root 节点的左子树，最后递归调用 preorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public List<Integer> preorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); preorder(root, res); return res; } public void preorder(TreeNode root, List<Integer> res) { if (root == null) { return; } res.add(root.val); preorder(root.left, res); preorder(root.right, res); } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
  • 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log n)，最坏情况下树呈现链状，为 O(n)。

  方法二：迭代

  思路与算法

  我们也可以用迭代的方式实现方法一的递归函数，两种方式是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其余的实现与细节都相同，具体可以参考下面的代码。

  • 初始化维护一个栈，将根节点入栈。

  • 当栈不为空时

  • • 弹出栈顶元素 node，将节点值加入结果数组中。
    • 若 node 的右子树不为空，右子树入栈。
    • 若 node 的左子树不为空，左子树入栈。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public List<Integer> preorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); if (root == null) { return res; } Deque<TreeNode> stack = new LinkedList<TreeNode>(); TreeNode node = root; while (!stack.isEmpty() || node != null) { while (node != null) { res.add(node.val); stack.push(node); node = node.left; } node = stack.pop(); node = node.right; } return res; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点数。每一个节点恰好被遍历一次。
  • 空间复杂度：O(n)，为迭代过程中显式栈的开销，平均情况下为 O(log n)，最坏情况下树呈现链状，为 O(n)。

  方法三：Morris 遍历

  思路与算法

  有一种巧妙的方法可以在线性时间内，只占用常数空间来实现前序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

  Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其前序遍历规则总结如下：

  1. 新建临时节点，令该节点为 root；
  2. 如果当前节点的左子节点为空，将当前节点加入答案，并遍历当前节点的右子节点；
  3. 如果当前节点的左子节点不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点：
     • 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为当前节点。然后将当前节点加入答案，并将前驱节点的右子节点更新为当前节点。当前节点更新为当前节点的左子节点。
     • 如果前驱节点的右子节点为当前节点，将它的右子节点重新设为空。当前节点更新为当前节点的右子节点。
  4. 重复步骤 2 和步骤 3，直到遍历结束。

  这样我们利用 Morris 遍历的方法，前序遍历该二叉树，即可实现线性时间与常数空间的遍历。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  class Solution { public List<Integer> preorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); if (root == null) { return res; } TreeNode p1 = root, p2 = null; while (p1 != null) { p2 = p1.left; if (p2 != null) { while (p2.right != null && p2.right != p1) { p2 = p2.right; } if (p2.right == null) { res.add(p1.val); p2.right = p1; p1 = p1.left; continue; } else { p2.right = null; } } else { res.add(p1.val); } p1 = p1.right; } return res; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点数。没有左子树的节点只被访问一次，有左子树的节点被访问两次。
  • 空间复杂度：O(1)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。

day40

94. 二叉树的中序遍历

• 题目

  给定一个二叉树的根节点 root ，返回 它的 中序 遍历 。

  示例 1：

  

  1 2	输入：root = [1,null,2,3] 输出：[1,3,2]

  示例 2：

  1 2	输入：root = [] 输出：[]

  示例 3：

  1 2	输入：root = [1] 输出：[1]

  提示：

  • 树中节点数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

  进阶: 递归算法很简单，你可以通过迭代算法完成吗？

• 解法

  方法一：递归

  思路与算法

  首先我们需要了解什么是二叉树的中序遍历：按照访问左子树——根节点——右子树的方式遍历这棵树，而在访问左子树或者右子树的时候我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。

  定义 inorder(root) 表示当前遍历到 root 节点的答案，那么按照定义，我们只要递归调用 inorder(root.left) 来遍历 root 节点的左子树，然后将 root 节点的值加入答案，再递归调用inorder(root.right) 来遍历 root 节点的右子树即可，递归终止的条件为碰到空节点。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); inorder(root, res); return res; } public void inorder(TreeNode root, List<Integer> res) { if (root == null) { return; } inorder(root.left, res); res.add(root.val); inorder(root.right, res); } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
  • 空间复杂度：O(n)。空间复杂度取决于递归的栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。

  方法二：迭代

  思路与算法

  方法一的递归函数我们也可以用迭代的方式实现，两种方式是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其他都相同，具体实现可以看下面的代码。

  • 初始化一个空栈。

  • 当【根节点不为空】或者【栈不为空】时，从根节点开始

  • • 若当前节点有左子树，一直遍历左子树，每次将当前节点压入栈中。
    • 若当前节点无左子树，从栈中弹出该节点，尝试访问该节点的右子树。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); Deque<TreeNode> stk = new LinkedList<TreeNode>(); while (root != null || !stk.isEmpty()) { while (root != null) { stk.push(root); root = root.left; } root = stk.pop(); res.add(root.val); root = root.right; } return res; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉树节点的个数。二叉树的遍历中每个节点会被访问一次且只会被访问一次。
  • 空间复杂度：O(n)。空间复杂度取决于栈深度，而栈深度在二叉树为一条链的情况下会达到 O(n) 的级别。

  方法三：Morris 中序遍历

  思路与算法

  Morris 遍历算法是另一种遍历二叉树的方法，它能将非递归的中序遍历空间复杂度降为 O(1)。

  Morris 遍历算法整体步骤如下（假设当前遍历到的节点为 x）：

  1. 如果 x 无左孩子，先将 x 的值加入答案数组，再访问 x 的右孩子，即x*=*x.right。
  2. 如果 x 有左孩子，则找到 x 左子树上最右的节点（即左子树中序遍历的最后一个节点，x 在中序遍历中的前驱节点），我们记为predecessor. 根据predecessor的右孩子是否为空，进行如下操作。
     • 如果 predecessor 的右孩子为空，则将其右孩子指向 x，然后访问 x 的左孩子，即 x = x.left。
     • 如果 predecessor 的右孩子不为空，则此时其右孩子指向 x，说明我们已经遍历完 x 的左子树，我们将 predecessor 的右孩子置空，将 x 的值加入答案数组，然后访问 x 的右孩子，即 x*=*x.right。
  3. 重复上述操作，直至访问完整棵树。

  其实整个过程我们就多做一步：假设当前遍历到的节点为 x，将 x 的左子树中最右边的节点的右孩子指向 x，这样在左子树遍历完成后我们通过这个指向走回了 x，且能通过这个指向知晓我们已经遍历完成了左子树，而不用再通过栈来维护，省去了栈的空间复杂度。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { public List<Integer> inorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); TreeNode predecessor = null; while (root != null) { if (root.left != null) { // predecessor 节点就是当前 root 节点向左走一步，然后一直向右走至无法走为止 predecessor = root.left; while (predecessor.right != null && predecessor.right != root) { predecessor = predecessor.right; } // 让 predecessor 的右指针指向 root，继续遍历左子树 if (predecessor.right == null) { predecessor.right = root; root = root.left; } // 说明左子树已经访问完了，我们需要断开链接 else { res.add(root.val); predecessor.right = null; root = root.right; } } // 如果没有左孩子，则直接访问右孩子 else { res.add(root.val); root = root.right; } } return res; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉搜索树的节点个数。Morris 遍历中每个节点会被访问两次，因此总时间复杂度为 O(2n)=O(n)。
  • 空间复杂度：O(1)。

day41

105. 从前序与中序遍历序列构造二叉树

• 题目

  给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

  示例 1:

  

  1 2	输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7] 输出: [3,9,20,null,null,15,7]

  示例 2:

  1 2	输入: preorder = [-1], inorder = [-1] 输出: [-1]

  提示:

  • 1 <= preorder.length <= 3000
  • inorder.length == preorder.length
  • -3000 <= preorder[i], inorder[i] <= 3000
  • preorder 和 inorder 均 无重复 元素
  • inorder 均出现在 preorder
  • preorder 保证 为二叉树的前序遍历序列
  • inorder 保证 为二叉树的中序遍历序列

• 解法

  二叉树前序遍历的顺序为：

  • 先遍历根节点；
  • 随后递归地遍历左子树；
  • 最后递归地遍历右子树。

  二叉树中序遍历的顺序为：

  • 先递归地遍历左子树；
  • 随后遍历根节点；
  • 最后递归地遍历右子树。

  在「递归」地遍历某个子树的过程中，我们也是将这颗子树看成一颗全新的树，按照上述的顺序进行遍历。挖掘「前序遍历」和「中序遍历」的性质，我们就可以得出本题的做法。

  方法一：递归

  思路

  对于任意一颗树而言，前序遍历的形式总是

  1	[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]

  即根节点总是前序遍历中的第一个节点。而中序遍历的形式总是

  1	[ [左子树的中序遍历结果], 根节点, [右子树的中序遍历结果] ]

  只要我们在中序遍历中定位到根节点，那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的，因此我们就可以对应到前序遍历的结果中，对上述形式中的所有左右括号进行定位。

  这样以来，我们就知道了左子树的前序遍历和中序遍历结果，以及右子树的前序遍历和中序遍历结果，我们就可以递归地对构造出左子树和右子树，再将这两颗子树接到根节点的左右位置。

  细节

  在中序遍历中对根节点进行定位时，一种简单的方法是直接扫描整个中序遍历的结果并找出根节点，但这样做的时间复杂度较高。我们可以考虑使用哈希表来帮助我们快速地定位根节点。对于哈希映射中的每个键值对，键表示一个元素（节点的值），值表示其在中序遍历中的出现位置。在构造二叉树的过程之前，我们可以对中序遍历的列表进行一遍扫描，就可以构造出这个哈希映射。在此后构造二叉树的过程中，我们就只需要 O(1) 的时间对根节点进行定位了。

  下面的代码给出了详细的注释。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

  class Solution { private Map<Integer, Integer> indexMap; public TreeNode myBuildTree(int[] preorder, int[] inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) { if (preorder_left > preorder_right) { return null; } // 前序遍历中的第一个节点就是根节点 int preorder_root = preorder_left; // 在中序遍历中定位根节点 int inorder_root = indexMap.get(preorder[preorder_root]); // 先把根节点建立出来 TreeNode root = new TreeNode(preorder[preorder_root]); // 得到左子树中的节点数目 int size_left_subtree = inorder_root - inorder_left; // 递归地构造左子树，并连接到根节点 // 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素 root.left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1); // 递归地构造右子树，并连接到根节点 // 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素 root.right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right); return root; } public TreeNode buildTree(int[] preorder, int[] inorder) { int n = preorder.length; // 构造哈希映射，帮助我们快速定位根节点 indexMap = new HashMap<Integer, Integer>(); for (int i = 0; i < n; i++) { indexMap.put(inorder[i], i); } return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1); } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  /** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func buildTree(preorder []int, inorder []int) *TreeNode { return dfs(preorder,inorder) } func dfs(preorder,inorder []int)*TreeNode{ if len(preorder)==0{ return nil } // fmt.Println(preorder[prel]) root:=&TreeNode{Val:preorder[0]}// 创建根节点 inRootIdx:=0//取中序遍历根节点索引 for ;inRootIdx<len(inorder);inRootIdx++{ if inorder[inRootIdx]==preorder[0]{ break } } root.Left = dfs(preorder[1:len(inorder[:inRootIdx])+1],inorder[:inRootIdx]) root.Right = dfs(preorder[len(inorder[:inRootIdx])+1:],inorder[inRootIdx+1:]) return root }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是树中的节点个数。
  • 空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，我们还需要使用 O(n) 的空间存储哈希映射，以及 O(h)（其中 h 是树的高度）的空间表示递归时栈空间。这里 h < n，所以总空间复杂度为 O(n)。

  方法二：迭代

  思路

  迭代法是一种非常巧妙的实现方法。

  对于前序遍历中的任意两个连续节点 u 和 v，根据前序遍历的流程，我们可以知道 u 和 v 只有两种可能的关系：

  • v 是 u 的左儿子。这是因为在遍历到 u 之后，下一个遍历的节点就是 u 的左儿子，即 v；
  • u 没有左儿子，并且 v 是 u 的某个祖先节点（或者 u 本身）的右儿子。如果 u 没有左儿子，那么下一个遍历的节点就是 u 的右儿子。如果 u 没有右儿子，我们就会向上回溯，直到遇到第一个有右儿子（且 u 不在它的右儿子的子树中）的节点 u_a，那么 v 就是 u_a 的右儿子。

  第二种关系看上去有些复杂。我们举一个例子来说明其正确性，并在例子中给出我们的迭代算法。

  例子

  我们以树

  1 2 3 4 5 6 7 8 9

  3 / \ 9 20 / / \ 8 15 7 / \ 5 10 / 4

  为例，它的前序遍历和中序遍历分别为

  1 2	preorder = [3, 9, 8, 5, 4, 10, 20, 15, 7] inorder = [4, 5, 8, 10, 9, 3, 15, 20, 7]

  我们用一个栈 stack 来维护「当前节点的所有还没有考虑过右儿子的祖先节点」，栈顶就是当前节点。也就是说，只有在栈中的节点才可能连接一个新的右儿子。同时，我们用一个指针 index 指向中序遍历的某个位置，初始值为 0。index 对应的节点是「当前节点不断往左走达到的最终节点」，这也是符合中序遍历的，它的作用在下面的过程中会有所体现。

  首先我们将根节点 3 入栈，再初始化 index 所指向的节点为 4，随后对于前序遍历中的每个节点，我们依次判断它是栈顶节点的左儿子，还是栈中某个节点的右儿子。

  • 我们遍历 9。9 一定是栈顶节点 3 的左儿子。我们使用反证法，假设 9 是 3 的右儿子，那么 3 没有左儿子，index 应该恰好指向 3，但实际上为 4，因此产生了矛盾。所以我们将 9 作为 3 的左儿子，并将 9 入栈。

    • stack = [3, 9]
    • index -> inorder[0] = 4

  • 我们遍历 8，5 和 4。同理可得它们都是上一个节点（栈顶节点）的左儿子，所以它们会依次入栈。

    • stack = [3, 9, 8, 5, 4]
    • index -> inorder[0] = 4

  • 我们遍历 10，这时情况就不一样了。我们发现 index 恰好指向当前的栈顶节点 4，也就是说 4 没有左儿子，那么 10 必须为栈中某个节点的右儿子。那么如何找到这个节点呢？栈中的节点的顺序和它们在前序遍历中出现的顺序是一致的，而且每一个节点的右儿子都还没有被遍历过，那么这些节点的顺序和它们在中序遍历中出现的顺序一定是相反的。

    这是因为栈中的任意两个相邻的节点，前者都是后者的某个祖先。并且我们知道，栈中的任意一个节点的右儿子还没有被遍历过，说明后者一定是前者左儿子的子树中的节点，那么后者就先于前者出现在中序遍历中。

    因此我们可以把 index 不断向右移动，并与栈顶节点进行比较。如果 index 对应的元素恰好等于栈顶节点，那么说明我们在中序遍历中找到了栈顶节点，所以将 index 增加 1 并弹出栈顶节点，直到 index 对应的元素不等于栈顶节点。按照这样的过程，我们弹出的最后一个节点 x 就是 10 的双亲节点，这是因为 10 出现在了 x 与 x 在栈中的下一个节点的中序遍历之间，因此 10 就是 x 的右儿子。

    回到我们的例子，我们会依次从栈顶弹出 4，5 和 8，并且将 index 向右移动了三次。我们将 10 作为最后弹出的节点 8 的右儿子，并将 10 入栈。

    • stack = [3, 9, 10]
    • index -> inorder[3] = 10

  • 我们遍历 20。同理，index 恰好指向当前栈顶节点 10，那么我们会依次从栈顶弹出 10，9 和 3，并且将 index 向右移动了三次。我们将 20 作为最后弹出的节点 3 的右儿子，并将 20 入栈。

    • stack = [20]
    • index -> inorder[6] = 15

  • 我们遍历 15，将 15 作为栈顶节点 20 的左儿子，并将 15 入栈。

    • stack = [20, 15]
    • index -> inorder[6] = 15

  • 我们遍历 7。index 恰好指向当前栈顶节点 15，那么我们会依次从栈顶弹出 15 和 20，并且将 index 向右移动了两次。我们将 7 作为最后弹出的节点 20 的右儿子，并将 7 入栈。

    • stack = [7]
    • index -> inorder[8] = 7

  此时遍历结束，我们就构造出了正确的二叉树。

  算法

  我们归纳出上述例子中的算法流程：

  • 我们用一个栈和一个指针辅助进行二叉树的构造。初始时栈中存放了根节点（前序遍历的第一个节点），指针指向中序遍历的第一个节点；
  • 我们依次枚举前序遍历中除了第一个节点以外的每个节点。如果 index 恰好指向栈顶节点，那么我们不断地弹出栈顶节点并向右移动 index，并将当前节点作为最后一个弹出的节点的右儿子；如果 index 和栈顶节点不同，我们将当前节点作为栈顶节点的左儿子；
  • 无论是哪一种情况，我们最后都将当前的节点入栈。

  最后得到的二叉树即为答案。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public TreeNode buildTree(int[] preorder, int[] inorder) { if (preorder == null || preorder.length == 0) { return null; } TreeNode root = new TreeNode(preorder[0]); Deque<TreeNode> stack = new LinkedList<TreeNode>(); stack.push(root); int inorderIndex = 0; for (int i = 1; i < preorder.length; i++) { int preorderVal = preorder[i]; TreeNode node = stack.peek(); if (node.val != inorder[inorderIndex]) { node.left = new TreeNode(preorderVal); stack.push(node.left); } else { while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) { node = stack.pop(); inorderIndex++; } node.right = new TreeNode(preorderVal); stack.push(node.right); } } return root; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是树中的节点个数。
  • 空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，我们还需要使用 O(h)（其中 h 是树的高度）的空间存储栈。这里 h < n，所以（在最坏情况下）总空间复杂度为 O(n)。

day42

106. 从中序与后序遍历序列构造二叉树

• 题目

  给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。

  示例 1:

  

  1 2	输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3] 输出：[3,9,20,null,null,15,7]

  示例 2:

  1 2	输入：inorder = [-1], postorder = [-1] 输出：[-1]

  提示:

  • 1 <= inorder.length <= 3000
  • postorder.length == inorder.length
  • -3000 <= inorder[i], postorder[i] <= 3000
  • inorder 和 postorder 都由 不同 的值组成
  • postorder 中每一个值都在 inorder 中
  • inorder 保证是树的中序遍历
  • postorder 保证是树的后序遍历

• 解法

  方法一：递归

  我们可以发现后序遍历的数组最后一个元素代表的即为根节点。知道这个性质后，我们可以利用已知的根节点信息在中序遍历的数组中找到根节点所在的下标，然后根据其将中序遍历的数组分成左右两部分，左边部分即左子树，右边部分为右子树，针对每个部分可以用同样的方法继续递归下去构造。

  

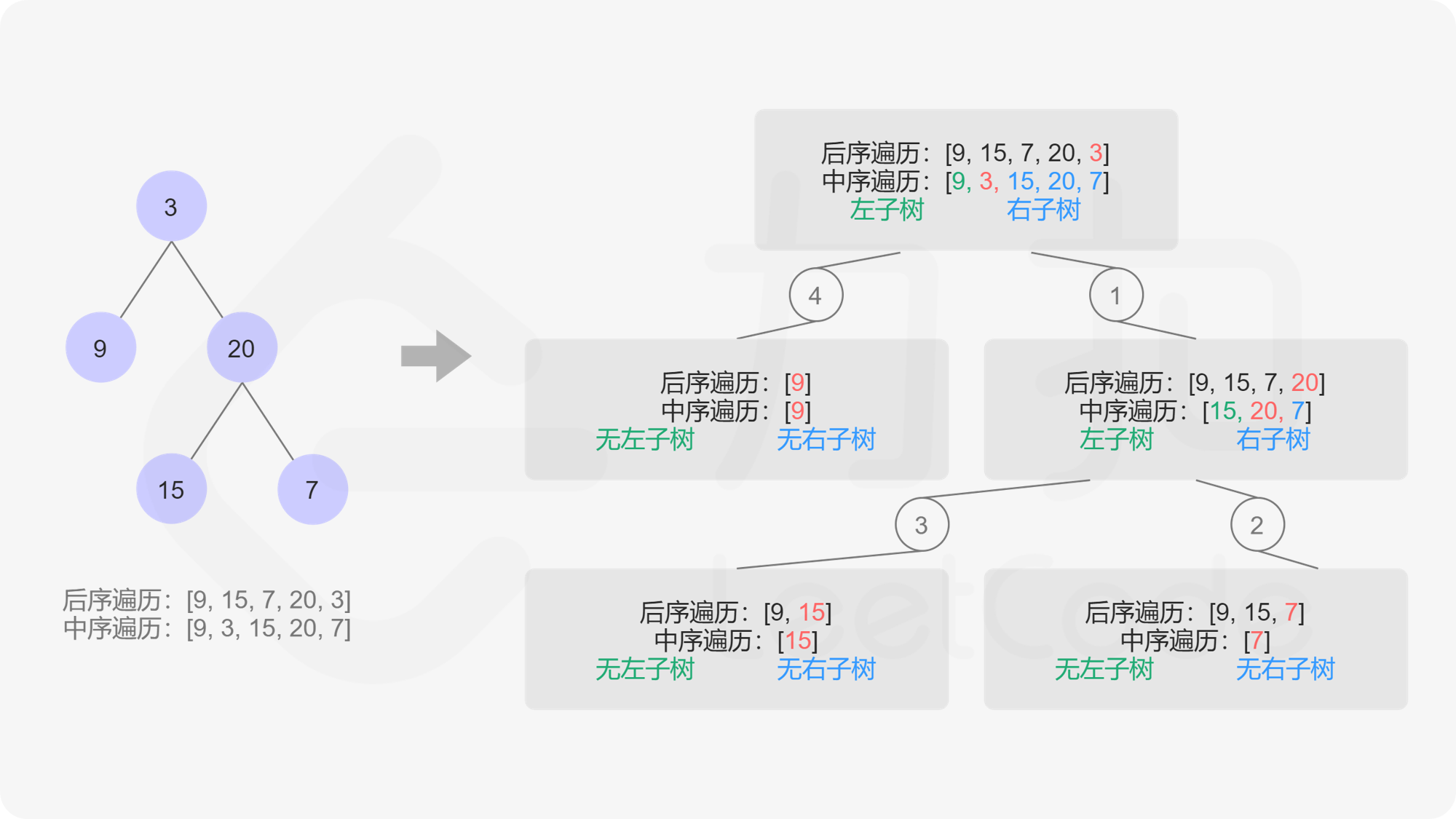
  算法

  • 为了高效查找根节点元素在中序遍历数组中的下标，我们选择创建哈希表来存储中序序列，即建立一个（元素，下标）键值对的哈希表。
  • 定义递归函数 helper(in_left, in_right) 表示当前递归到中序序列中当前子树的左右边界，递归入口为helper(0, n - 1) ：
    • 如果 in_left > in_right，说明子树为空，返回空节点。
    • 选择后序遍历的最后一个节点作为根节点。
    • 利用哈希表 O(1) 查询当根节点在中序遍历中下标为 index。从 in_left 到 index - 1 属于左子树，从 index + 1 到 in_right 属于右子树。
    • 根据后序遍历逻辑，递归创建右子树 helper(index + 1, in_right) 和左子树 helper(in_left, index - 1)。注意这里有需要先创建右子树，再创建左子树的依赖关系。可以理解为在后序遍历的数组中整个数组是先存储左子树的节点，再存储右子树的节点，最后存储根节点，如果按每次选择「后序遍历的最后一个节点」为根节点，则先被构造出来的应该为右子树。
    • 返回根节点 root

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45

  class Solution { int post_idx; int[] postorder; int[] inorder; Map<Integer, Integer> idx_map = new HashMap<Integer, Integer>(); public TreeNode helper(int in_left, int in_right) { // 如果这里没有节点构造二叉树了，就结束 if (in_left > in_right) { return null; } // 选择 post_idx 位置的元素作为当前子树根节点 int root_val = postorder[post_idx]; TreeNode root = new TreeNode(root_val); // 根据 root 所在位置分成左右两棵子树 int index = idx_map.get(root_val); // 下标减一 post_idx--; // 构造右子树 root.right = helper(index + 1, in_right); // 构造左子树 root.left = helper(in_left, index - 1); return root; } public TreeNode buildTree(int[] inorder, int[] postorder) { this.postorder = postorder; this.inorder = inorder; // 从后序遍历的最后一个元素开始 post_idx = postorder.length - 1; // 建立（元素，下标）键值对的哈希表 int idx = 0; for (Integer val : inorder) { idx_map.put(val, idx++); } return helper(0, inorder.length - 1); } } // 或者

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是树中的节点个数。
  • 空间复杂度：O(n)。我们需要使用 O(n) 的空间存储哈希表，以及 O(h)（其中 h 是树的高度）的空间表示递归时栈空间。这里 h < n，所以总空间复杂度为 O(n)。

  方法二：迭代

  思路

  迭代法是一种非常巧妙的实现方法。迭代法的实现基于以下两点发现。

  • 如果将中序遍历反序，则得到反向的中序遍历，即每次遍历右孩子，再遍历根节点，最后遍历左孩子。
  • 如果将后序遍历反序，则得到反向的前序遍历，即每次遍历根节点，再遍历右孩子，最后遍历左孩子。

  「反向」的意思是交换遍历左孩子和右孩子的顺序，即反向的遍历中，右孩子在左孩子之前被遍历。

  因此可以使用和「105. 从前序与中序遍历序列构造二叉树」的迭代方法类似的方法构造二叉树。

  对于后序遍历中的任意两个连续节点 u 和 v（在后序遍历中，u 在 v 的前面），根据后序遍历的流程，我们可以知道 u 和 v 只有两种可能的关系：

  • u 是 v 的右儿子。这是因为在遍历到 u 之后，下一个遍历的节点就是 u 的双亲节点，即 v；
  • v 没有右儿子，并且 u 是 v 的某个祖先节点（或者 v 本身）的左儿子。如果 v 没有右儿子，那么上一个遍历的节点就是 v 的左儿子。如果 v 没有左儿子，则从 v 开始向上遍历 v 的祖先节点，直到遇到一个有左儿子（且 v 不在它的左儿子的子树中）的节点 v_a，那么 u 就是 v_a 的左儿子。

  第二种关系看上去有些复杂。我们举一个例子来说明其正确性，并在例子中给出我们的迭代算法。

  例子

  我们以树

  1 2 3 4 5 6 7 8 9

  3 / \ 9 20 / \ \ 15 10 7 / \ 5 8 \ 4

  为例，它的中序遍历和后序遍历分别为

  1 2	inorder = [15, 9, 10, 3, 20, 5, 7, 8, 4] postorder = [15, 10, 9, 5, 4, 8, 7, 20, 3]

  我们用一个栈 stack 来维护「当前节点的所有还没有考虑过左儿子的祖先节点」，栈顶就是当前节点。也就是说，只有在栈中的节点才可能连接一个新的左儿子。同时，我们用一个指针 index 指向中序遍历的某个位置，初始值为 n - 1，其中 n 为数组的长度。index 对应的节点是「当前节点不断往右走达到的最终节点」，这也是符合反向中序遍历的，它的作用在下面的过程中会有所体现。

  首先我们将根节点 3 入栈，再初始化 index 所指向的节点为 4，随后对于后序遍历中的每个节点，我们依次判断它是栈顶节点的右儿子，还是栈中某个节点的左儿子。

  • 我们遍历 20。20 一定是栈顶节点 3 的右儿子。我们使用反证法，假设 20 是 3 的左儿子，因为 20 和 3 中间不存在其他的节点，那么 3 没有右儿子，index 应该恰好指向 3，但实际上为 4，因此产生了矛盾。所以我们将 20 作为 3 的右儿子，并将 20 入栈。

    • stack = [3, 20]
    • index -> inorder[8] = 4

  • 我们遍历 7，8 和 4。同理可得它们都是上一个节点（栈顶节点）的右儿子，所以它们会依次入栈。

    • stack = [3, 20, 7, 8, 4]
    • index -> inorder[8] = 4

  • 我们遍历 5，这时情况就不一样了。我们发现 index 恰好指向当前的栈顶节点 4，也就是说 4 没有右儿子，那么 5 必须为栈中某个节点的左儿子。那么如何找到这个节点呢？栈中的节点的顺序和它们在反向前序遍历中出现的顺序是一致的，而且每一个节点的左儿子都还没有被遍历过，那么这些节点的顺序和它们在反向中序遍历中出现的顺序一定是相反的。

    这是因为栈中的任意两个相邻的节点，前者都是后者的某个祖先。并且我们知道，栈中的任意一个节点的左儿子还没有被遍历过，说明后者一定是前者右儿子的子树中的节点，那么后者就先于前者出现在反向中序遍历中。

    因此我们可以把 index 不断向左移动，并与栈顶节点进行比较。如果 index 对应的元素恰好等于栈顶节点，那么说明我们在反向中序遍历中找到了栈顶节点，所以将 index 减少 1 并弹出栈顶节点，直到 index 对应的元素不等于栈顶节点。按照这样的过程，我们弹出的最后一个节点 x 就是 5 的双亲节点，这是因为 5 出现在了 x 与 x 在栈中的下一个节点的反向中序遍历之间，因此 5 就是 x 的左儿子。

    回到我们的例子，我们会依次从栈顶弹出 4，8 和 7，并且将 index 向左移动了三次。我们将 5 作为最后弹出的节点 7 的左儿子，并将 5 入栈。

    • stack = [3, 20, 5]
    • index -> inorder[5] = 5

  • 我们遍历 9。同理，index 恰好指向当前栈顶节点 5，那么我们会依次从栈顶弹出 5，20 和 3，并且将 index 向左移动了三次。我们将 9 作为最后弹出的节点 3 的左儿子，并将 9 入栈。

    • stack = [9]
    • index -> inorder[2] = 10

  • 我们遍历 10，将 10 作为栈顶节点 9 的右儿子，并将 10 入栈。

    • stack = [9, 10]
    • index -> inorder[2] = 10

  • 我们遍历 15。index 恰好指向当前栈顶节点 10，那么我们会依次从栈顶弹出 10 和 9，并且将 index 向左移动了两次。我们将 15 作为最后弹出的节点 9 的左儿子，并将 15 入栈。

    • stack = [15]
    • index -> inorder[0] = 15

  此时遍历结束，我们就构造出了正确的二叉树。

  算法

  我们归纳出上述例子中的算法流程：

  • 我们用一个栈和一个指针辅助进行二叉树的构造。初始时栈中存放了根节点（后序遍历的最后一个节点），指针指向中序遍历的最后一个节点；
  • 我们依次枚举后序遍历中除了第一个节点以外的每个节点。如果 index 恰好指向栈顶节点，那么我们不断地弹出栈顶节点并向左移动 index，并将当前节点作为最后一个弹出的节点的左儿子；如果 index 和栈顶节点不同，我们将当前节点作为栈顶节点的右儿子；
  • 无论是哪一种情况，我们最后都将当前的节点入栈。

  最后得到的二叉树即为答案。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public TreeNode buildTree(int[] inorder, int[] postorder) { if (postorder == null || postorder.length == 0) { return null; } TreeNode root = new TreeNode(postorder[postorder.length - 1]); Deque<TreeNode> stack = new LinkedList<TreeNode>(); stack.push(root); int inorderIndex = inorder.length - 1; for (int i = postorder.length - 2; i >= 0; i--) { int postorderVal = postorder[i]; TreeNode node = stack.peek(); if (node.val != inorder[inorderIndex]) { node.right = new TreeNode(postorderVal); stack.push(node.right); } else { while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) { node = stack.pop(); inorderIndex--; } node.left = new TreeNode(postorderVal); stack.push(node.left); } } return root; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是树中的节点个数。
  • 空间复杂度：O(n)，我们需要使用 O(h)（其中 h 是树的高度）的空间存储栈。这里 h < n，所以（在最坏情况下）总空间复杂度为 O(n)。

day43

145. 二叉树的后序遍历

• 题目

  给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

  示例 1：

  

  1 2	输入：root = [1,null,2,3] 输出：[3,2,1]

  示例 2：

  1 2	输入：root = [] 输出：[]

  示例 3：

  1 2	输入：root = [1] 输出：[1]

  提示：

  • 树中节点的数目在范围 [0, 100] 内
  • -100 <= Node.val <= 100

  **进阶：**递归算法很简单，你可以通过迭代算法完成吗？

• 解法

  方法一：递归

  思路与算法

  首先我们需要了解什么是二叉树的后序遍历：按照访问左子树——右子树——根节点的方式遍历这棵树，而在访问左子树或者右子树的时候，我们按照同样的方式遍历，直到遍历完整棵树。因此整个遍历过程天然具有递归的性质，我们可以直接用递归函数来模拟这一过程。

  定义 postorder(root) 表示当前遍历到 root 节点的答案。按照定义，我们只要递归调用 postorder(root->left) 来遍历 root 节点的左子树，然后递归调用 postorder(root->right) 来遍历 root 节点的右子树，最后将 root 节点的值加入答案即可，递归终止的条件为碰到空节点。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); postorder(root, res); return res; } public void postorder(TreeNode root, List<Integer> res) { if (root == null) { return; } postorder(root.left, res); postorder(root.right, res); res.add(root.val); } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
  • 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log n)，最坏情况下树呈现链状，为 O(n)。

  方法二：迭代

  思路与算法

  我们也可以用迭代的方式实现方法一的递归函数，两种方式是等价的，区别在于递归的时候隐式地维护了一个栈，而我们在迭代的时候需要显式地将这个栈模拟出来，其余的实现与细节都相同，具体可以参考下面的代码。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); if (root == null) { return res; } Deque<TreeNode> stack = new LinkedList<TreeNode>(); TreeNode prev = null; while (root != null || !stack.isEmpty()) { while (root != null) { stack.push(root); root = root.left; } root = stack.pop(); if (root.right == null || root.right == prev) { res.add(root.val); prev = root; root = null; } else { stack.push(root); root = root.right; } } return res; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
  • 空间复杂度：O(n)，为迭代过程中显式栈的开销，平均情况下为 O(log n)，最坏情况下树呈现链状，为 O(n)。

  方法三：Morris 遍历

  思路与算法

  有一种巧妙的方法可以在线性时间内，只占用常数空间来实现后序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

  Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其后序遍历规则总结如下：

  1. 新建临时节点，令该节点为 root；
  2. 如果当前节点的左子节点为空，则遍历当前节点的右子节点；
  3. 如果当前节点的左子节点不为空，在当前节点的左子树中找到当前节点在中序遍历下的前驱节点；
     • 如果前驱节点的右子节点为空，将前驱节点的右子节点设置为当前节点，当前节点更新为当前节点的左子节点。
     • 如果前驱节点的右子节点为当前节点，将它的右子节点重新设为空。倒序输出从当前节点的左子节点到该前驱节点这条路径上的所有节点。当前节点更新为当前节点的右子节点。
  4. 重复步骤 2 和步骤 3，直到遍历结束。

  这样我们利用 Morris 遍历的方法，后序遍历该二叉搜索树，即可实现线性时间与常数空间的遍历。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> res = new ArrayList<Integer>(); if (root == null) { return res; } TreeNode p1 = root, p2 = null; while (p1 != null) { p2 = p1.left; if (p2 != null) { while (p2.right != null && p2.right != p1) { p2 = p2.right; } if (p2.right == null) { p2.right = p1; p1 = p1.left; continue; } else { p2.right = null; addPath(res, p1.left); } } p1 = p1.right; } addPath(res, root); return res; } public void addPath(List<Integer> res, TreeNode node) { int count = 0; while (node != null) { ++count; res.add(node.val); node = node.right; } int left = res.size() - count, right = res.size() - 1; while (left < right) { int temp = res.get(left); res.set(left, res.get(right)); res.set(right, temp); left++; right--; } } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树的节点数。没有左子树的节点只被访问一次，有左子树的节点被访问两次。
  • 空间复杂度：O(1)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。

day44

102. 二叉树的层序遍历

• 题目

  给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

  示例 1：

  

  1 2	输入：root = [3,9,20,null,null,15,7] 输出：[[3],[9,20],[15,7]]

  示例 2：

  1 2	输入：root = [1] 输出：[[1]]

  示例 3：

  1 2	输入：root = [] 输出：[]

  提示：

  • 树中节点数目在范围 [0, 2000] 内
  • -1000 <= Node.val <= 1000

• 解法

  解法一：深度优先

  采用递归方法来找出层序序列。思路：我们知道，遍历递归地遍历二叉树是往深处走，我们只需要在往深处走的时候，将相同深度的节点放到一起即可。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class Solution { public List<List<Integer>> levelOrder(TreeNode root) { if (root==null) return new ArrayList<>(); List<List<Integer>> lls =new ArrayList<>(); doSome(root,1,lls); return lls; } // 递归层序遍历的秘诀：深度相同的节点放到同一个list public void doSome(TreeNode node,int depth,List<List<Integer>> lls){ // 当前深度下没有对应的“层list”，就创建 if(lls.size()<depth) { lls.add(new ArrayList<Integer>()); } //在同一深度，把节点加上去 lls.get(depth-1).add(node.val); if(node.left!=null) doSome(node.left,depth+1,lls); if(node.right!=null) doSome(node.right,depth+1,lls); } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  /** * Definition for a binary tree node. * type TreeNode struct { * Val int * Left *TreeNode * Right *TreeNode * } */ func levelOrder(root *TreeNode) [][]int { ans := [][]int{} if root==nil { return ans } var dfs func(root *TreeNode,depth int) dfs = func(root *TreeNode,depth int){ if root==nil{ return } if len(ans)<depth+1{ ans=append(ans,[]int{}) } ans[depth]=append(ans[depth],root.Val) dfs(root.Left,depth+1) dfs(root.Right,depth+1) return } dfs(root,0) return ans }

解法二：广度优先搜索

解题思路

本文将会讲解为什么这道题适合用广度优先搜索（BFS），以及 BFS 适用于什么样的场景。

DFS（深度优先搜索）和 BFS（广度优先搜索）就像孪生兄弟，提到一个总是想起另一个。然而在实际使用中，我们用 DFS 的时候远远多于 BFS。那么，是不是 BFS 就没有什么用呢？

如果我们使用 DFS/BFS 只是为了遍历一棵树、一张图上的所有结点的话，那么 DFS 和 BFS 的能力没什么差别，我们当然更倾向于更方便写、空间复杂度更低的 DFS 遍历。不过，某些使用场景是 DFS 做不到的，只能使用 BFS 遍历。这就是本文要介绍的两个场景：「层序遍历」、「最短路径」。

本文包括以下内容：

• DFS 与 BFS 的特点比较
• BFS 的适用场景
• 如何用 BFS 进行层序遍历
• 如何用 BFS 求解最短路径问题

DFS 与 BFS

让我们先看看在二叉树上进行 DFS 遍历和 BFS 遍历的代码比较。

DFS 遍历使用递归：

BFS 遍历使用队列数据结构：

只是比较两段代码的话，最直观的感受就是：DFS 遍历的代码比 BFS 简洁太多了！这是因为递归的方式隐含地使用了系统的 栈，我们不需要自己维护一个数据结构。如果只是简单地将二叉树遍历一遍，那么 DFS 显然是更方便的选择。

虽然 DFS 与 BFS 都是将二叉树的所有结点遍历了一遍，但它们遍历结点的顺序不同。

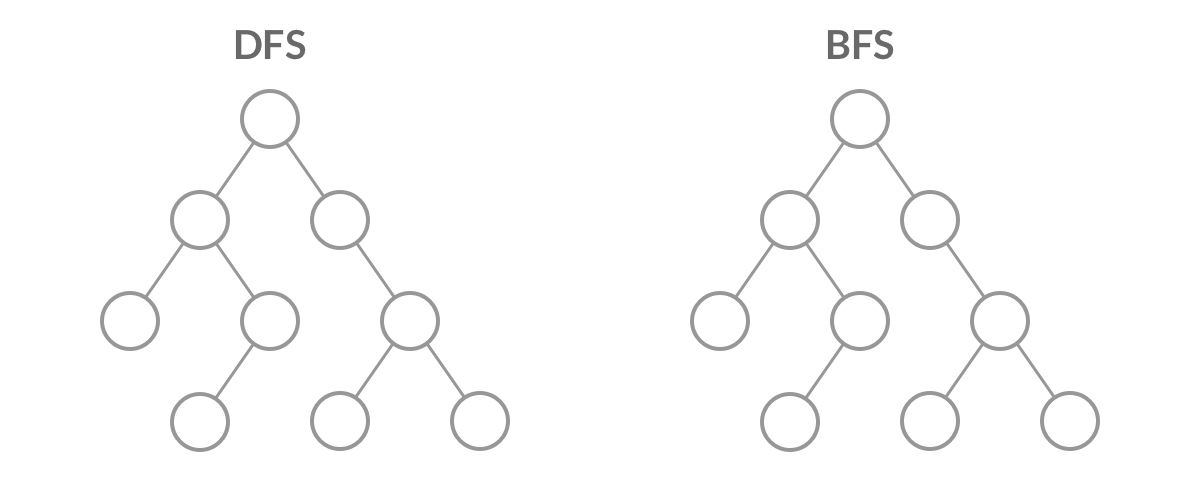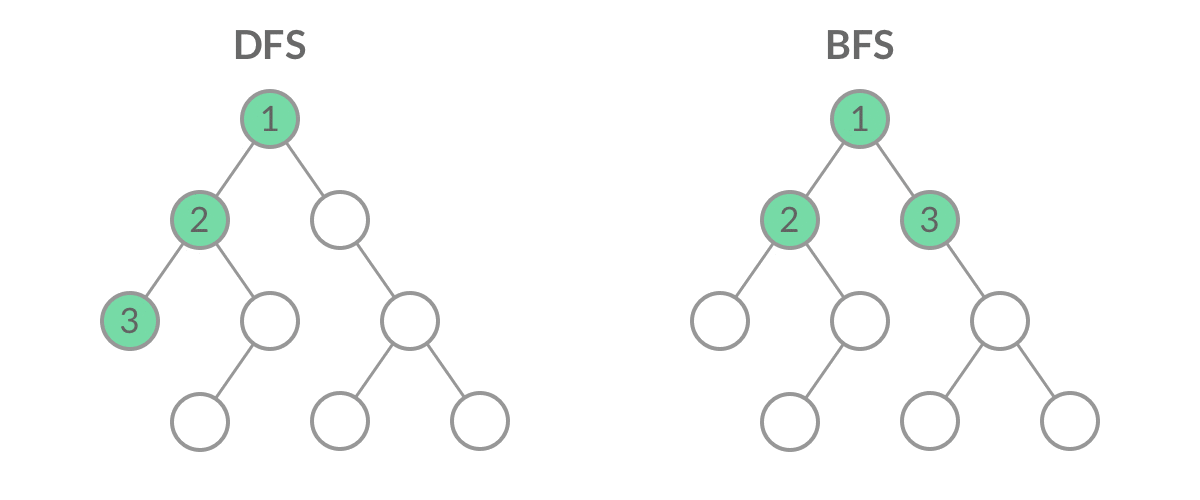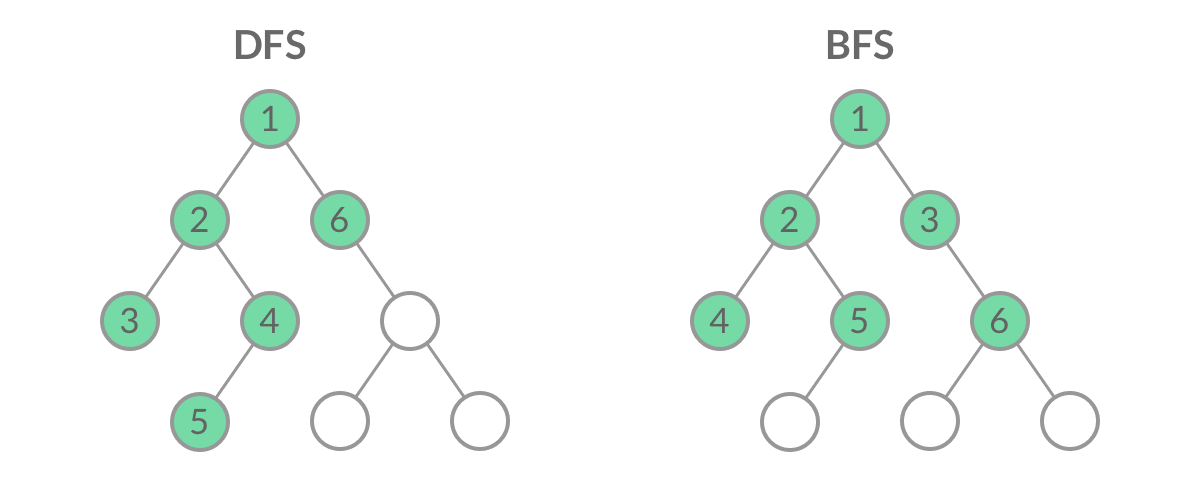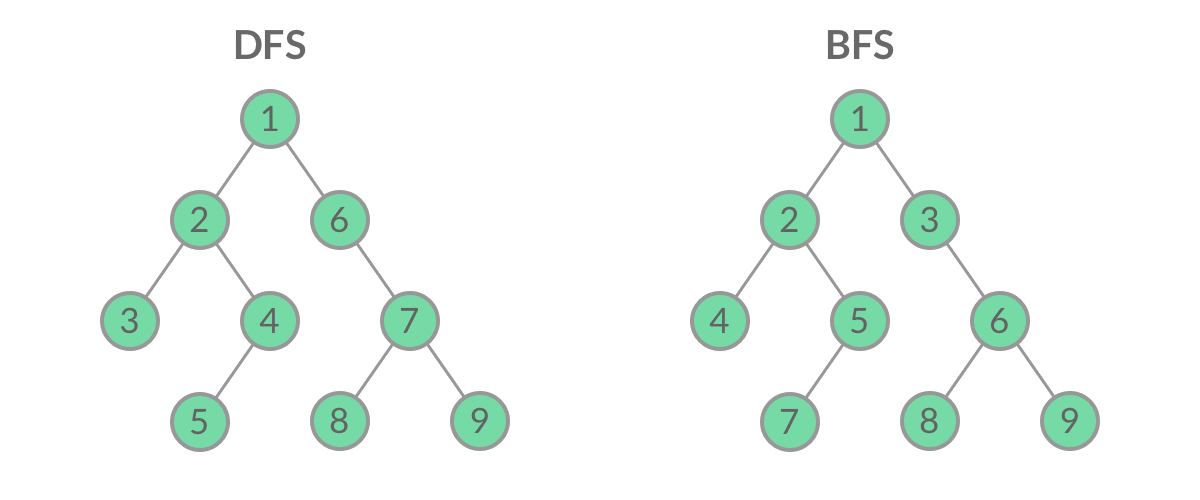
这个遍历顺序也是 BFS 能够用来解「层序遍历」、「最短路径」问题的根本原因。下面，我们结合几道例题来讲讲 BFS 是如何求解层序遍历和最短路径问题的。

BFS 的应用一：层序遍历

BFS 的层序遍历应用就是本题了：

LeetCode 102. Binary Tree Level Order Traversal 二叉树的层序遍历（Medium）

给定一个二叉树，返回其按层序遍历得到的节点值。层序遍历即逐层地、从左到右访问所有结点。

什么是层序遍历呢？简单来说，层序遍历就是把二叉树分层，然后每一层从左到右遍历：

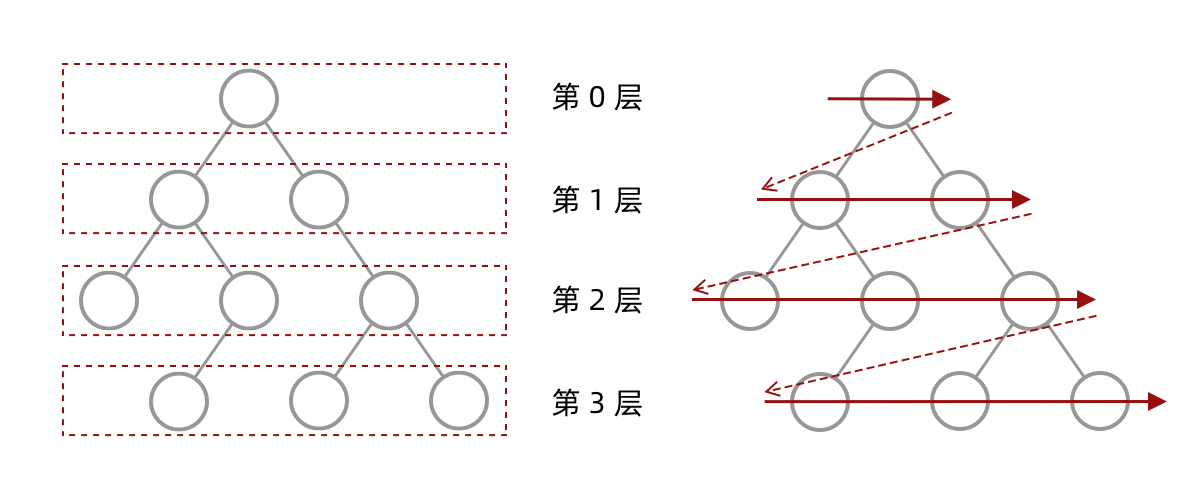
乍一看来，这个遍历顺序和 BFS 是一样的，我们可以直接用 BFS 得出层序遍历结果。然而，层序遍历要求的输入结果和 BFS 是不同的。层序遍历要求我们区分每一层，也就是返回一个二维数组。而 BFS 的遍历结果是一个一维数组，无法区分每一层。

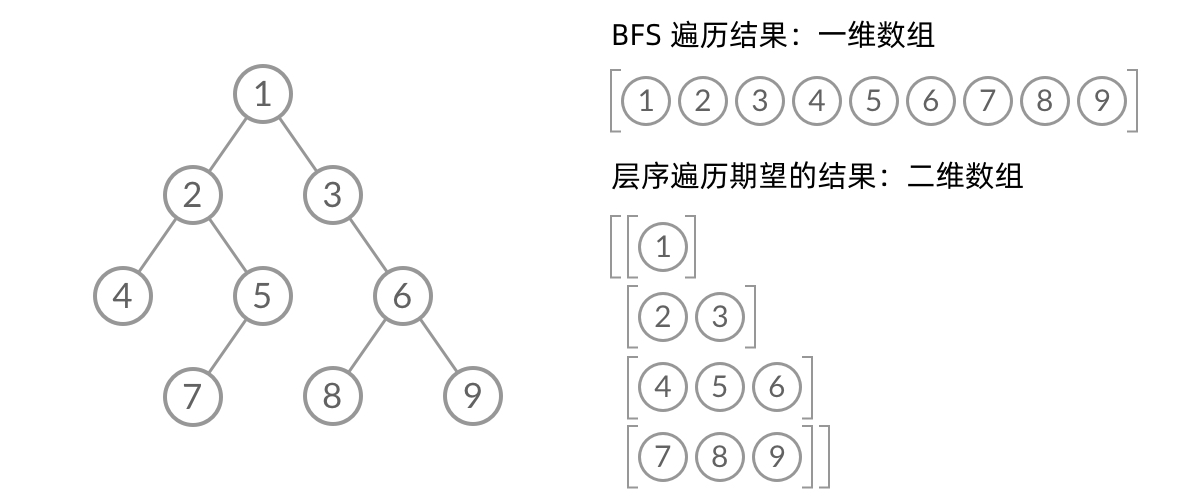
那么，怎么给 BFS 遍历的结果分层呢？我们首先来观察一下 BFS 遍历的过程中，结点进队列和出队列的过程：

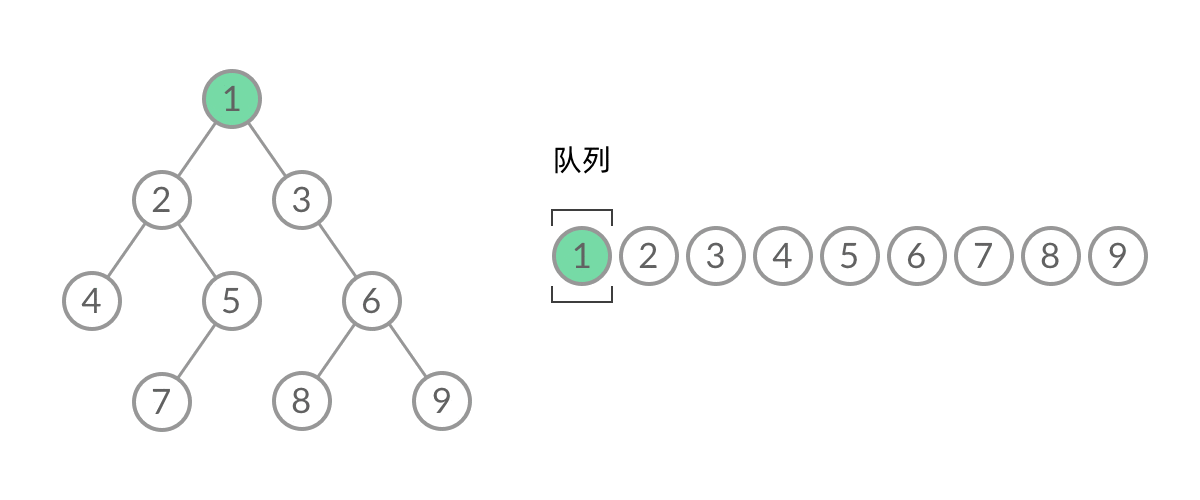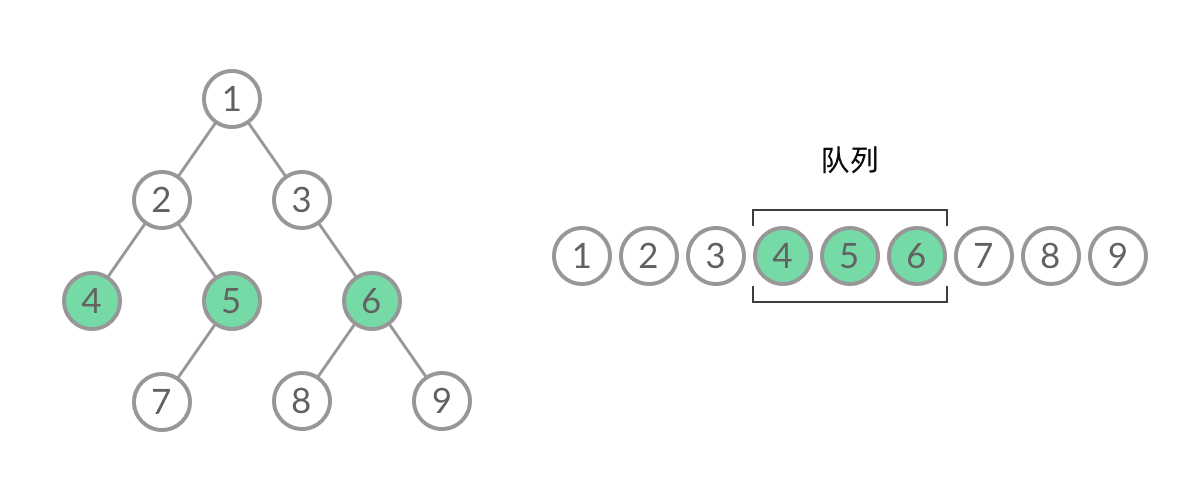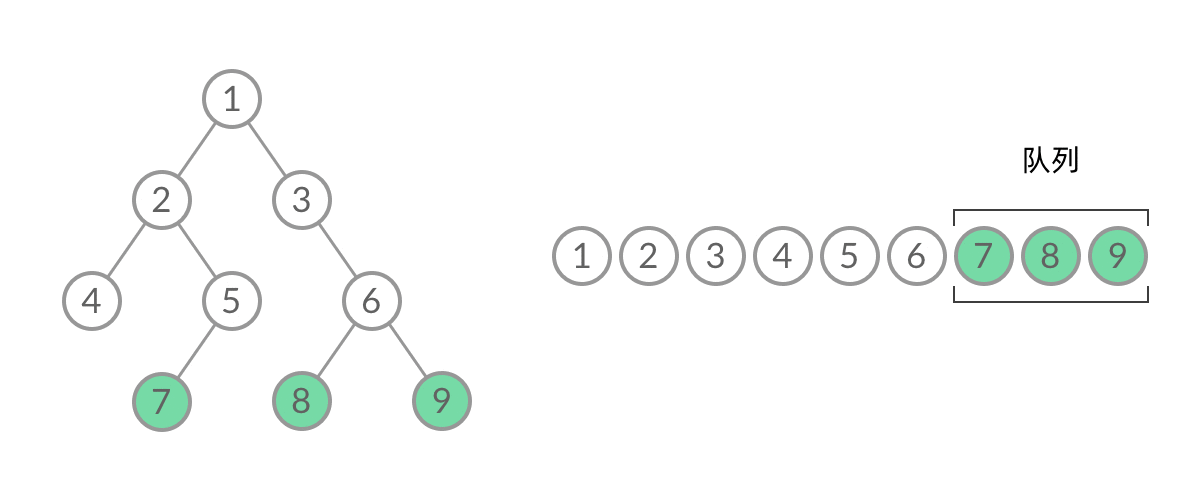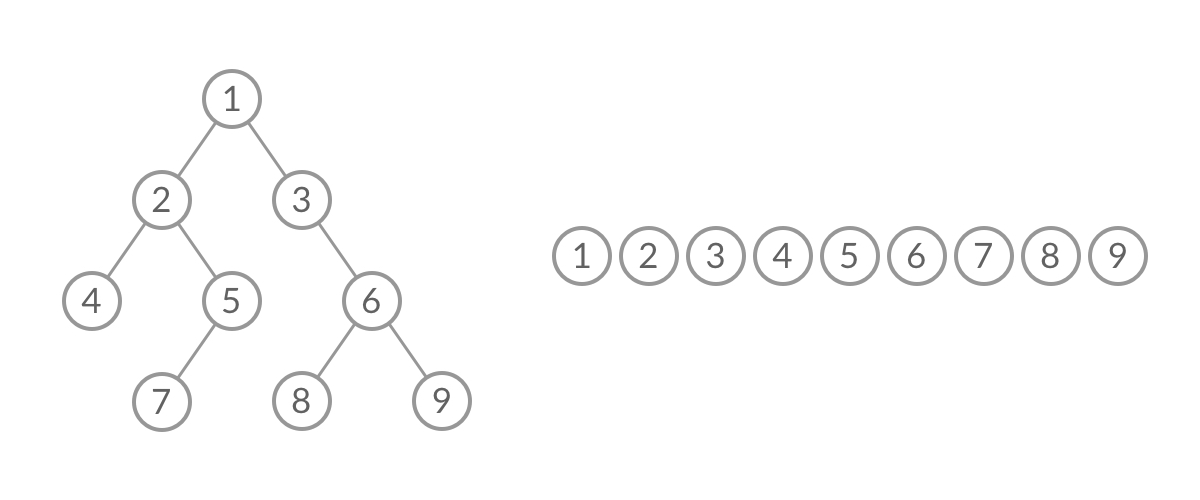
截取 BFS 遍历过程中的某个时刻：

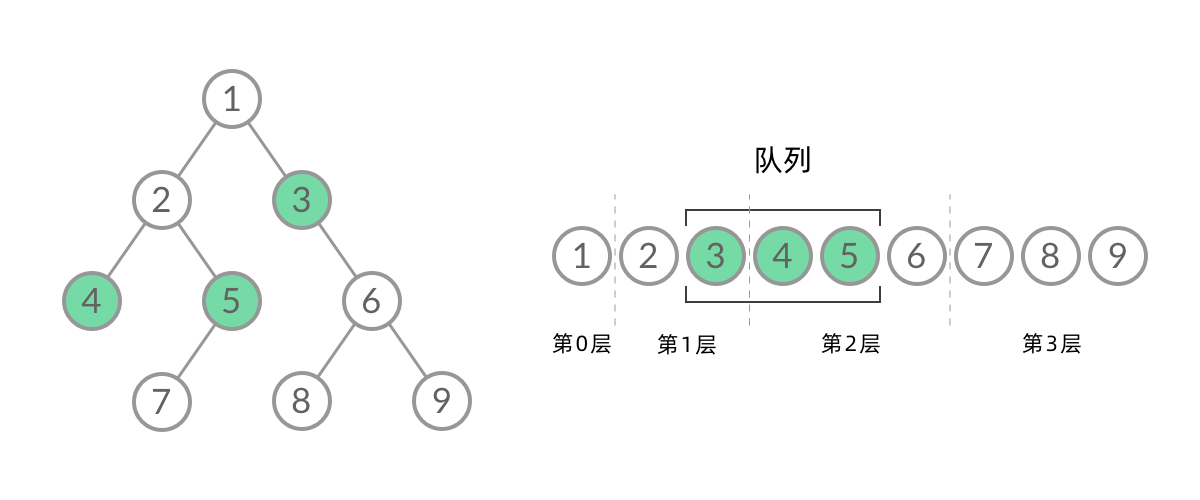
可以看到，此时队列中的结点是 3、4、5，分别来自第 1 层和第 2 层。这个时候，第 1 层的结点还没出完，第 2 层的结点就进来了，而且两层的结点在队列中紧挨在一起，我们无法区分队列中的结点来自哪一层。

因此，我们需要稍微修改一下代码，在每一层遍历开始前，先记录队列中的结点数量 n（也就是这一层的结点数量），然后一口气处理完这一层的 n 个结点。

这样，我们就将 BFS 遍历改造成了层序遍历。在遍历的过程中，结点进队列和出队列的过程为：

可以看到，在 while 循环的每一轮中，都是将当前层的所有结点出队列，再将下一层的所有结点入队列，这样就实现了层序遍历。

最终我们得到的题解代码为：

BFS 的应用二：最短路径

在一棵树中，一个结点到另一个结点的路径是唯一的，但在图中，结点之间可能有多条路径，其中哪条路最近呢？这一类问题称为最短路径问题。最短路径问题也是 BFS 的典型应用，而且其方法与层序遍历关系密切。

在二叉树中，BFS 可以实现一层一层的遍历。在图中同样如此。从源点出发，BFS 首先遍历到第一层结点，到源点的距离为 1，然后遍历到第二层结点，到源点的距离为 2…… 可以看到，用 BFS 的话，距离源点更近的点会先被遍历到，这样就能找到到某个点的最短路径了。

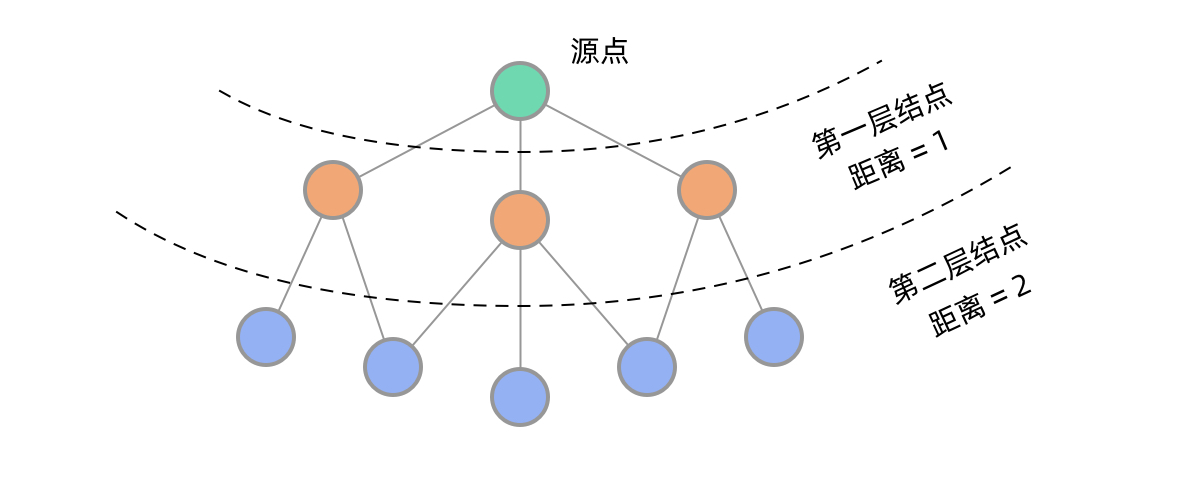
小贴士：

很多同学一看到「最短路径」，就条件反射地想到「Dijkstra 算法」。为什么 BFS 遍历也能找到最短路径呢？

这是因为，Dijkstra 算法解决的是带权最短路径问题，而我们这里关注的是无权最短路径问题。也可以看成每条边的权重都是 1。这样的最短路径问题，用 BFS 求解就行了。

在面试中，你可能更希望写 BFS 而不是 Dijkstra 。毕竟，敢保证自己能写对 Dijkstra 算法的人不多。

最短路径问题属于图算法。由于图的表示和描述比较复杂，本文用比较简单的网格结构代替。网格结构是一种特殊的图，它的表示和遍历都比较简单，适合作为练习题。在 LeetCode 中，最短路径问题也以网格结构为主。

最短路径例题讲解

LeetCode 1162. As Far from Land as Possible 离开陆地的最远距离（Medium）

你现在手里有一份大小为 n×n 的地图网格 grid，上面的每个单元格都标记为 0 或者 1，其中 0 代表海洋，1 代表陆地，请你找出一个海洋区域，这个海洋区域到离它最近的陆地区域的距离是最大的。

我们这里说的距离是「曼哈顿距离」。(x_0, y_0) 和 (x_1, y_1) 这两个区域之间的距离是 |x_0 - x_1| + |y_0 - y_1| 。

如果我们的地图上只有陆地或者海洋，请返回 -1。

这道题就是一个在网格结构中求最短路径的问题。同时，它也是一个「岛屿问题」，即用网格中的 1 和 0 表示陆地和海洋，模拟出若干个岛屿。

在上一篇文章中，我们介绍了网格结构的基本概念，以及网格结构中的 DFS 遍历。其中一些概念和技巧也可以用在 BFS 遍历中：

• 格子 (r, c) 的相邻四个格子为：(r-1, c)、(r+1, c)、(r, c-1) 和 (r, c+1)；
• 使用函数 inArea 判断当前格子的坐标是否在网格范围内；
• 将遍历过的格子标记为 2，避免重复遍历。

对于网格结构的性质、网格结构的 DFS 遍历技巧不是很了解的同学，可以复习一下上一篇文章：LeetCode 例题精讲 | 12 岛屿问题：网格结构中的 DFS。

上一篇文章讲过了网格结构 DFS 遍历，这篇文章正好讲解一下网格结构的 BFS 遍历。要解最短路径问题，我们首先要写出层序遍历的代码，仿照上面的二叉树层序遍历代码，类似地可以写出网格层序遍历：

以上的层序遍历代码有几个注意点：

• 队列中的元素类型是 int[] 数组，每个数组的长度为 2，包含格子的行坐标和列坐标。
• 为了避免重复遍历，这里使用到了和 DFS 遍历一样的技巧：把已遍历的格子标记为 2。注意：我们在将格子放入队列之前就将其标记为 2。想一想，这是为什么？
• 在将格子放入队列之前就检查其坐标是否在网格范围内，避免将「不存在」的格子放入队列。

这段网格遍历代码还有一些可以优化的地方。由于一个格子有四个相邻的格子，代码中判断了四遍格子坐标的合法性，代码稍微有点啰嗦。我们可以用一个 moves 数组存储相邻格子的四个方向：

然后把四个 if 判断变成一个循环：

写好了层序遍历的代码，接下来我们看看如何来解决本题中的最短路径问题。

这道题要找的是距离陆地最远的海洋格子。假设网格中只有一个陆地格子，我们可以从这个陆地格子出发做层序遍历，直到所有格子都遍历完。最终遍历了几层，海洋格子的最远距离就是几。

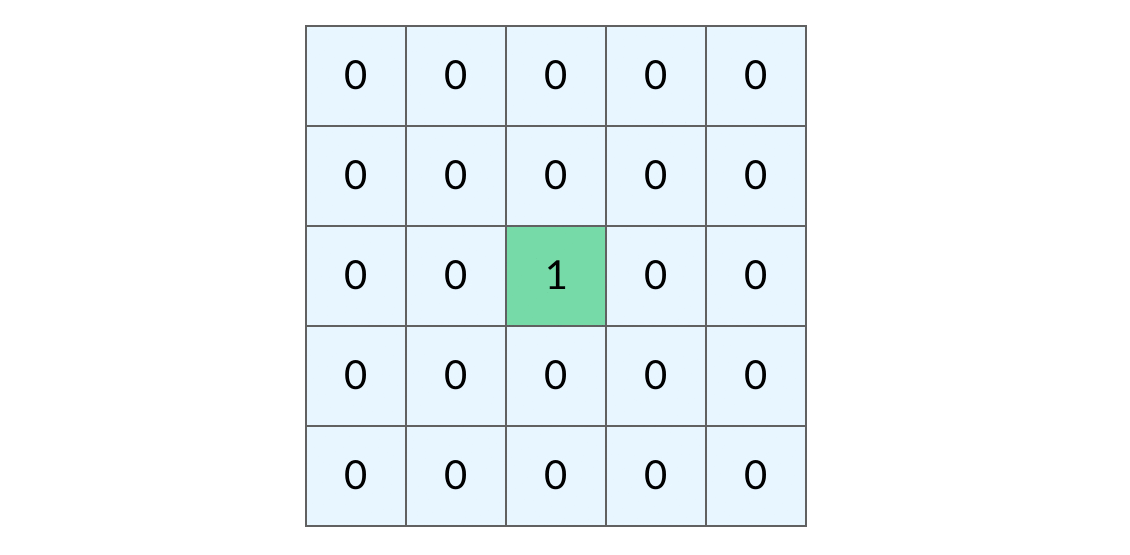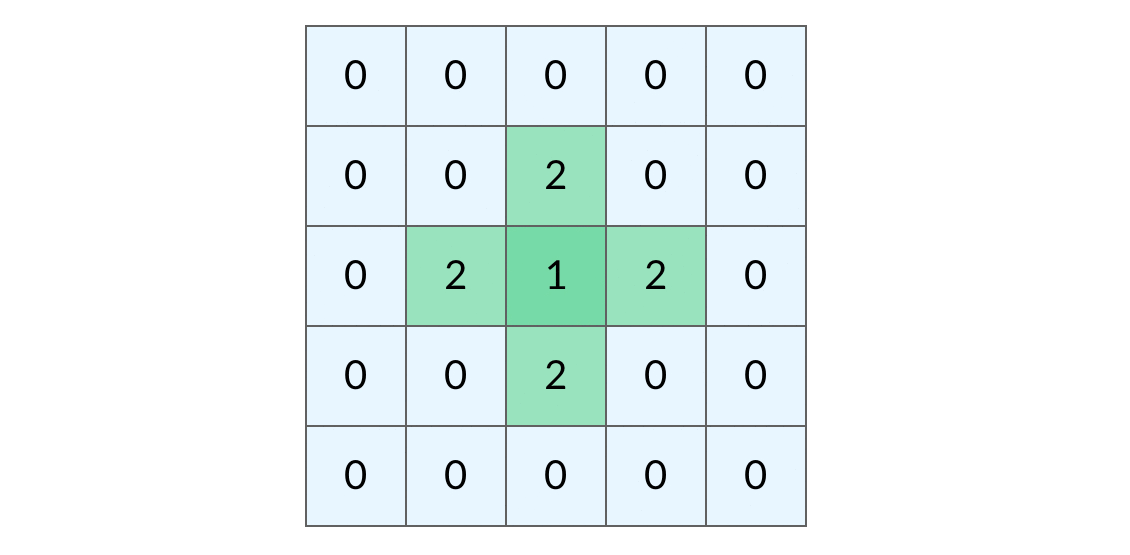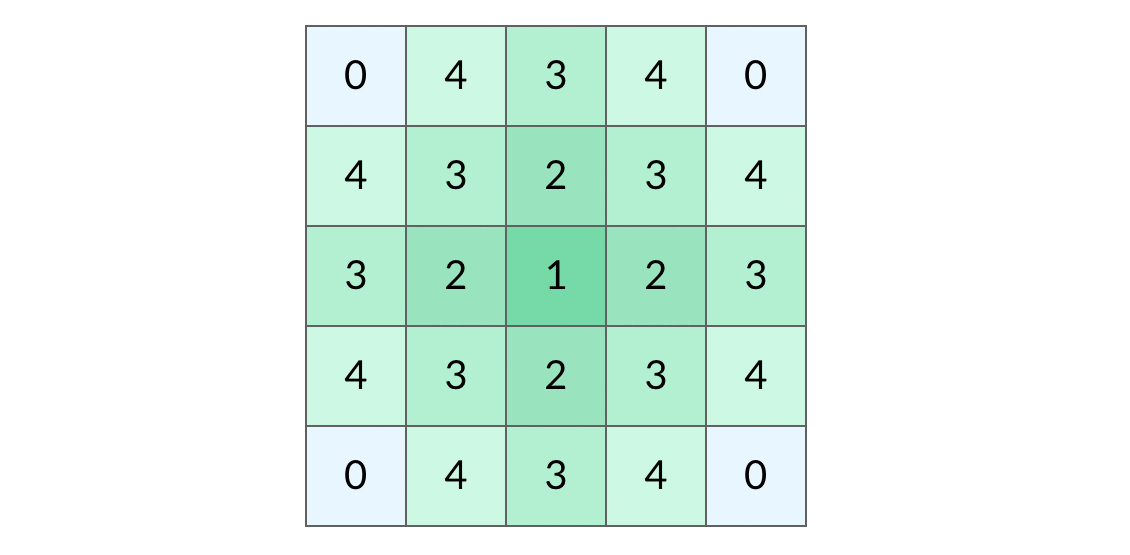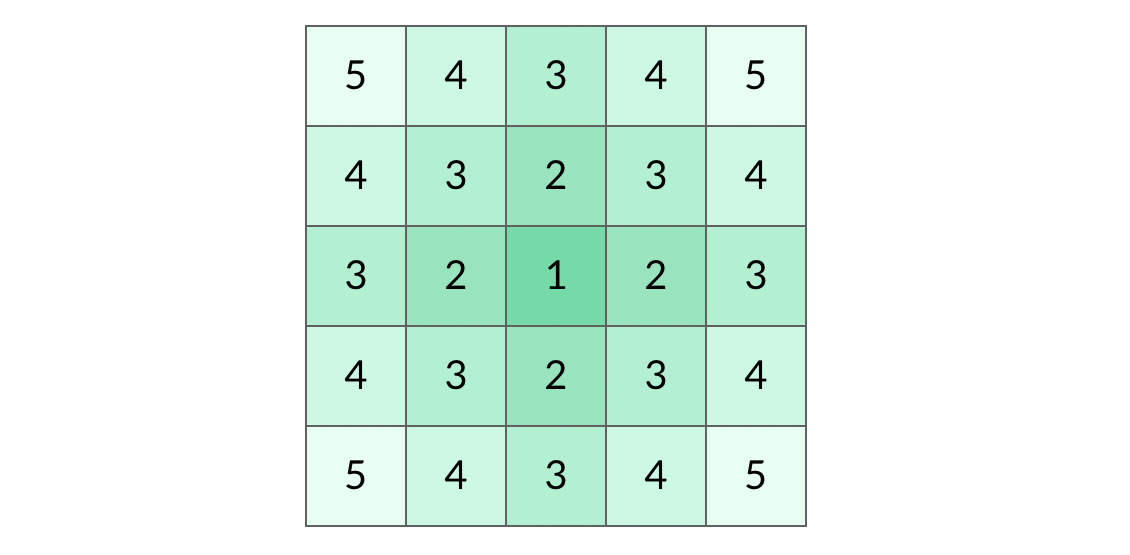
那么有多个陆地格子的时候怎么办呢？一种方法是将每个陆地格子都作为起点做一次层序遍历，但是这样的时间开销太大。

BFS 完全可以以多个格子同时作为起点。我们可以把所有的陆地格子同时放入初始队列，然后开始层序遍历，这样遍历的效果如下图所示：

这种遍历方法实际上叫做「多源 BFS」。多源 BFS 的定义不是今天讨论的重点，你只需要记住多源 BFS 很方便，只需要把多个源点同时放入初始队列即可。

需要注意的是，虽然上面的图示用 1、2、3、4 表示层序遍历的层数，但是在代码中，我们不需要给每个遍历到的格子标记层数，只需要用一个 distance 变量记录当前的遍历的层数（也就是到陆地格子的距离）即可。

最终，我们得到的题解代码为：

总结

可以看到，「BFS 遍历」、「层序遍历」、「最短路径」实际上是递进的关系。在 BFS 遍历的基础上区分遍历的每一层，就得到了层序遍历。在层序遍历的基础上记录层数，就得到了最短路径。

BFS 遍历是一类很值得反复体会和练习的题目。一方面，BFS 遍历是一个经典的基础算法，需要重点掌握。另一方面，我们需要能根据题意分析出题目是要求最短路径，知道是要做 BFS 遍历。

本文讲解的只是两道非常典型的例题。LeetCode 中还有许多层序遍历和最短路径的题目

层序遍历的一些变种题目：

• LeetCode 103. Binary Tree Zigzag Level Order Traversal 之字形层序遍历
• LeetCode 199. Binary Tree Right Side View 找每一层的最右结点
• LeetCode 515. Find Largest Value in Each Tree Row 计算每一层的最大值
• LeetCode 637. Average of Levels in Binary Tree 计算每一层的平均值

对于最短路径问题，还有两道题目也是求网格结构中的最短路径，和我们讲解的距离岛屿的最远距离非常类似：

• LeetCode 542. 01 Matrix
• LeetCode 994. Rotting Oranges

还有一道在真正的图结构中求最短路径的问题：

• LeetCode 310. Minimum Height Trees

经过了本文的讲解，相信解决这些题目也不是难事。

day45

107. 二叉树的层序遍历 II

• 题目

  给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

  示例 1：

  

  1 2	输入：root = [3,9,20,null,null,15,7] 输出：[[15,7],[9,20],[3]]

  示例 2：

  1 2	输入：root = [1] 输出：[[1]]

  示例 3：

  1 2	输入：root = [] 输出：[]

  提示：

  • 树中节点数目在范围 [0, 2000] 内
  • -1000 <= Node.val <= 1000

• 解法

  解法一：无脑广度优先

  在前面一题的思路上，转换一下：只需要在添加当层遍历list时，插入头部即可。

  题解

  解法二：不优雅的深度优先遍历

  将上题设深度优先产生的序列反序即可。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  class Solution { void level(TreeNode root, int index, List<List<Integer>> res) { // 当前行对应的列表不存在，加一个空列表 if(res.size() < index) { res.add(new ArrayList<Integer>()); } // 将当前节点的值加入当前行的 res 中 res.get(index-1).add(root.val); // 递归处理左子树 if(root.left != null) { level(root.left, index+1, res); } // 递归处理右子树 if(root.right != null) { level(root.right, index+1, res); } } public List<List<Integer>> levelOrderBottom(TreeNode root) { if(root == null) { return new ArrayList<List<Integer>>(); } List<List<Integer>> list = new ArrayList<List<Integer>>(); List<List<Integer>> res = new ArrayList<List<Integer>>(); level(root, 1, list); for(int i = list.size()-1; i >= 0; i--){ res.add(list.get(i)); } return res; } }

day46

199. 二叉树的右视图

• 题目

  给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

  示例 1:

  

  1 2	输入: [1,2,3,null,5,null,4] 输出: [1,3,4]

  示例 2:

  1 2	输入: [1,null,3] 输出: [1,3]

  示例 3:

  1 2	输入: [] 输出: []

  提示:

  • 二叉树的节点个数的范围是 [0,100]
  • -100 <= Node.val <= 100

• 解法

  BFS

  思路： 利用 BFS 进行层次遍历，记录下每层的最后一个元素。 时间复杂度： O(N)，每个节点都入队出队了 1 次。 空间复杂度： O(N)，使用了额外的队列空间。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  class Solution { public List<Integer> rightSideView(TreeNode root) { if(root == null) return new ArrayList<Integer>(); Queue<TreeNode> queue = new LinkedList<>(); List<Integer> ls =new ArrayList<>(); queue.offer(root); while(!queue.isEmpty()){ int size = queue.size(); while(size>0){ TreeNode node = queue.poll(); if(size==1) ls.add(node.val);// 层序遍历是最右边的节点最后被遍历 if(node.left!=null) queue.offer(node.left); if(node.right!=null) queue.offer(node.right); size--; } } return ls; } }

  DFS （时间100%）

  思路： 我们按照 「根结点 -> 右子树 -> 左子树」 的顺序访问，就可以保证每层都是最先访问最右边的节点的。

  （与先序遍历 「根结点 -> 左子树 -> 右子树」 正好相反，先序遍历每层最先访问的是最左边的节点）

  时间复杂度： O(N)，每个节点都访问了 1 次。 空间复杂度： O(N)，因为这不是一棵平衡二叉树，二叉树的深度最少是 logN, 最坏的情况下会退化成一条链表，深度就是 N，因此递归时使用的栈空间是 O(N) 的。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { List<Integer> res = new ArrayList<>(); public List<Integer> rightSideView(TreeNode root) { dfs(root, 0); // 从根节点开始访问，根节点深度是0 return res; } private void dfs(TreeNode root, int depth) { if (root == null) { return; } // 先访问 当前节点，再递归地访问 右子树 和 左子树。 if (depth == res.size()) { // 如果当前节点所在深度还没有出现在res里，说明在该深度下当前节点是第一个被访问的节点，因此将当前节点加入res中。 res.add(root.val); } depth++; dfs(root.right, depth); dfs(root.left, depth); } }

day47

429. N 叉树的层序遍历

• 题目

  给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

  树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

  示例 1：

  

  1 2	输入：root = [1,null,3,2,4,null,5,6] 输出：[[1],[3,2,4],[5,6]]

  示例 2：

  

  1 2	输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

  提示：

  • 树的高度不会超过 1000
  • 树的节点总数在 [0, 10^4] 之间

• 解法

  方法一：广度优先搜索

  思路与算法

  对于「层序遍历」的题目，我们一般使用广度优先搜索。在广度优先搜索的每一轮中，我们会遍历同一层的所有节点。

  具体地，我们首先把根节点 root 放入队列中，随后在广度优先搜索的每一轮中，我们首先记录下当前队列中包含的节点个数（记为 cnt），即表示上一层的节点个数。在这之后，我们从队列中依次取出节点，直到取出了上一层的全部 cnt 个节点为止。当取出节点 cur 时，我们将 cur 的值放入一个临时列表，再将 cur 的所有子节点全部放入队列中。

  当这一轮遍历完成后，临时列表中就存放了当前层所有节点的值。这样一来，当整个广度优先搜索完成后，我们就可以得到层序遍历的结果。

  细节

  需要特殊判断树为空的情况。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public List<List<Integer>> levelOrder(Node root) { if (root == null) return new ArrayList<>(); List<List<Integer>> lls = new ArrayList<>(); lls.add(new ArrayList<>()); lls.get(0).add(root.val); Queue<Node> queue = new LinkedList<>(root.children); while (!queue.isEmpty()) { int size = queue.size(); List<Integer> ls = new ArrayList<>(); while (size > 0) { Node node = queue.poll(); ls.add(node.val); if (node.children != null) queue.addAll(node.children); size--; } lls.add(ls); } return lls; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是树中包含的节点个数。在广度优先搜索的过程中，我们需要遍历每一个节点恰好一次。
  • 空间复杂度：O(n)，即为队列需要使用的空间。在最坏的情况下，树只有两层，且最后一层有 n-1 个节点，此时就需要 O(n) 的空间。

day48

637. 二叉树的层平均值

• 题目

  给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

  示例 1：

  

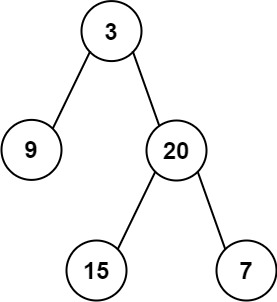
  1 2 3 4

  输入：root = [3,9,20,null,null,15,7] 输出：[3.00000,14.50000,11.00000] 解释：第 0 层的平均值为 3,第 1 层的平均值为 14.5,第 2 层的平均值为 11 。 因此返回 [3, 14.5, 11] 。

  示例 2:

  

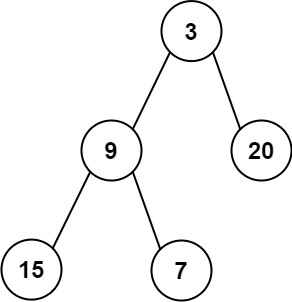
  1 2	输入：root = [3,9,20,15,7] 输出：[3.00000,14.50000,11.00000]

  提示：

  • 树中节点数量在 [1, 104] 范围内
  • -231 <= Node.val <= 231 - 1

• 解法

  方法一：深度优先搜索

  使用深度优先搜索计算二叉树的层平均值，需要维护两个数组，counts 用于存储二叉树的每一层的节点数，sums 用于存储二叉树的每一层的节点值之和。搜索过程中需要记录当前节点所在层，如果访问到的节点在第 i 层，则将 counts[i] 的值加 1，并将该节点的值加到 sums[i]。

  遍历结束之后，第 i 层的平均值即为 sums[i]/counts[i]。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  class Solution { public List<Double> averageOfLevels(TreeNode root) { List<Integer> counts = new ArrayList<Integer>(); List<Double> sums = new ArrayList<Double>(); dfs(root, 0, counts, sums); List<Double> averages = new ArrayList<Double>(); int size = sums.size(); for (int i = 0; i < size; i++) { averages.add(sums.get(i) / counts.get(i)); } return averages; } public void dfs(TreeNode root, int level, List<Integer> counts, List<Double> sums) { if (root == null) { return; } if (level < sums.size()) { sums.set(level, sums.get(level) + root.val); counts.set(level, counts.get(level) + 1); } else { sums.add(1.0 * root.val); counts.add(1); } dfs(root.left, level + 1, counts, sums); dfs(root.right, level + 1, counts, sums); } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。 深度优先搜索需要对每个节点访问一次，对于每个节点，维护两个数组的时间复杂度都是 O(1)，因此深度优先搜索的时间复杂度是 O(n)。 遍历结束之后计算每层的平均值的时间复杂度是 O(h)，其中 h 是二叉树的高度，任何情况下都满足 h≤n。 因此总时间复杂度是 O(n)。
  • 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度取决于两个数组的大小和递归调用的层数，两个数组的大小都等于二叉树的高度，递归调用的层数不会超过二叉树的高度，最坏情况下，二叉树的高度等于节点个数。

  方法二：广度优先搜索

  也可以使用广度优先搜索计算二叉树的层平均值。从根节点开始搜索，每一轮遍历同一层的全部节点，计算该层的节点数以及该层的节点值之和，然后计算该层的平均值。

  如何确保每一轮遍历的是同一层的全部节点呢？我们可以借鉴层次遍历的做法，广度优先搜索使用队列存储待访问节点，只要确保在每一轮遍历时，队列中的节点是同一层的全部节点即可。具体做法如下：

  • 初始时，将根节点加入队列；
  • 每一轮遍历时，将队列中的节点全部取出，计算这些节点的数量以及它们的节点值之和，并计算这些节点的平均值，然后将这些节点的全部非空子节点加入队列，重复上述操作直到队列为空，遍历结束。

  由于初始时队列中只有根节点，满足队列中的节点是同一层的全部节点，每一轮遍历时都会将队列中的当前层节点全部取出，并将下一层的全部节点加入队列，因此可以确保每一轮遍历的是同一层的全部节点。

  具体实现方面，可以在每一轮遍历之前获得队列中的节点数量 size，遍历时只遍历 size 个节点，即可满足每一轮遍历的是同一层的全部节点。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  class Solution { public List<Double> averageOfLevels(TreeNode root) { List<Double> averages = new ArrayList<Double>(); Queue<TreeNode> queue = new LinkedList<TreeNode>(); queue.offer(root); while (!queue.isEmpty()) { double sum = 0; int size = queue.size(); for (int i = 0; i < size; i++) { TreeNode node = queue.poll(); sum += node.val; TreeNode left = node.left, right = node.right; if (left != null) { queue.offer(left); } if (right != null) { queue.offer(right); } } averages.add(sum / size); } return averages; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。 广度优先搜索需要对每个节点访问一次，时间复杂度是 O(n)。 需要对二叉树的每一层计算平均值，时间复杂度是 O(h)，其中 h 是二叉树的高度，任何情况下都满足 h≤n。 因此总时间复杂度是 O(n)。
  • 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度取决于队列开销，队列中的节点个数不会超过 n。

day49

98. 验证二叉搜索树

• 题目

  给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

  有效 二叉搜索树定义如下：

  • 节点的左子树只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

  示例 1：

  

  1 2	输入：root = [2,1,3] 输出：true

  示例 2：

  

  1 2 3

  输入：root = [5,1,4,null,null,3,6] 输出：false 解释：根节点的值是 5 ，但是右子节点的值是 4 。

  提示：

  • 树中节点数目范围在[1, 104] 内
  • -2^31^ <= Node.val <= 2^31^ - 1

• 解法

  方法一: 递归

  思路和算法

  要解决这道题首先我们要了解二叉搜索树有什么性质可以给我们利用，由题目给出的信息我们可以知道：如果该二叉树的左子树不为空，则左子树上所有节点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；它的左右子树也为二叉搜索树。

  这启示我们设计一个递归函数 helper(root, lower, upper) 来递归判断，函数表示考虑以 root 为根的子树，判断子树中所有节点的值是否都在 (l,r) 的范围内（注意是开区间）。如果 root 节点的值 val 不在 (l,r) 的范围内说明不满足条件直接返回，否则我们要继续递归调用检查它的左右子树是否满足，如果都满足才说明这是一棵二叉搜索树。

  那么根据二叉搜索树的性质，在递归调用左子树时，我们需要把上界 upper 改为 root.val，即调用 helper(root.left, lower, root.val)，因为左子树里所有节点的值均小于它的根节点的值。同理递归调用右子树时，我们需要把下界 lower 改为 root.val，即调用 helper(root.right, root.val, upper)。

  函数递归调用的入口为 helper(root, -inf, +inf)， inf 表示一个无穷大的值。

  下图展示了算法如何应用在示例 2 上：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public boolean isValidBST(TreeNode root) { return isValidBST(root, Long.MIN_VALUE, Long.MAX_VALUE); } // 主要是递归过程中传递了左右子节点的值用于比较 public boolean isValidBST(TreeNode node, long lower, long upper) { if (node == null) { return true; } if (node.val <= lower || node.val >= upper) { return false; } return isValidBST(node.left, lower, node.val) && isValidBST(node.right, node.val, upper); } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉树的节点个数。在递归调用的时候二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n)。
  • 空间复杂度：O(n)，其中 n 为二叉树的节点个数。递归函数在递归过程中需要为每一层递归函数分配栈空间，所以这里需要额外的空间且该空间取决于递归的深度，即二叉树的高度。最坏情况下二叉树为一条链，树的高度为 n ，递归最深达到 n 层，故最坏情况下空间复杂度为 O(n) 。

  方法二：中序遍历+类似于单调栈

  思路和算法

  基于方法一中提及的性质，我们可以进一步知道二叉搜索树「中序遍历」得到的值构成的序列一定是升序的，这启示我们在中序遍历的时候实时检查当前节点的值是否大于前一个中序遍历到的节点的值即可。如果均大于说明这个序列是升序的，整棵树是二叉搜索树，否则不是，下面的代码我们使用栈来模拟中序遍历的过程。

  可能有读者不知道中序遍历是什么，我们这里简单提及。中序遍历是二叉树的一种遍历方式，它先遍历左子树，再遍历根节点，最后遍历右子树。而我们二叉搜索树保证了左子树的节点的值均小于根节点的值，根节点的值均小于右子树的值，因此中序遍历以后得到的序列一定是升序序列。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public boolean isValidBST(TreeNode root) { Deque<TreeNode> stack = new LinkedList<TreeNode>(); double inorder = -Double.MAX_VALUE; while (!stack.isEmpty() || root != null) { while (root != null) { stack.push(root); root = root.left; } root = stack.pop(); // 如果中序遍历得到的节点的值小于等于前一个 inorder，说明不是二叉搜索树 if (root.val <= inorder) { return false; } inorder = root.val; root = root.right; } return true; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉树的节点个数。二叉树的每个节点最多被访问一次，因此时间复杂度为 O(n) 。
  • 空间复杂度：O(n)，其中 n 为二叉树的节点个数。栈最多存储 n 个节点，因此需要额外的 O(n) 的空间。

day50

108. 将有序数组转换为二叉搜索树

• 题目

  给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

  高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

  示例 1：

  

  1 2 3

  输入：nums = [-10,-3,0,5,9] 输出：[0,-3,9,-10,null,5] 解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：

  示例 2：

  

  1 2 3

  输入：nums = [1,3] 输出：[3,1] 解释：[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。

  提示：

  • 1 <= nums.length <= 104
  • -104 <= nums[i] <= 104
  • nums 按 严格递增 顺序排列

• 解法

  前言

  二叉搜索树的中序遍历是升序序列，题目给定的数组是按照升序排序的有序数组，因此可以确保数组是二叉搜索树的中序遍历序列。

  **给定二叉搜索树的中序遍历，是否可以唯一地确定二叉搜索树？答案是否定的。**如果没有要求二叉搜索树的高度平衡，则任何一个数字都可以作为二叉搜索树的根节点，因此可能的二叉搜索树有多个。

  

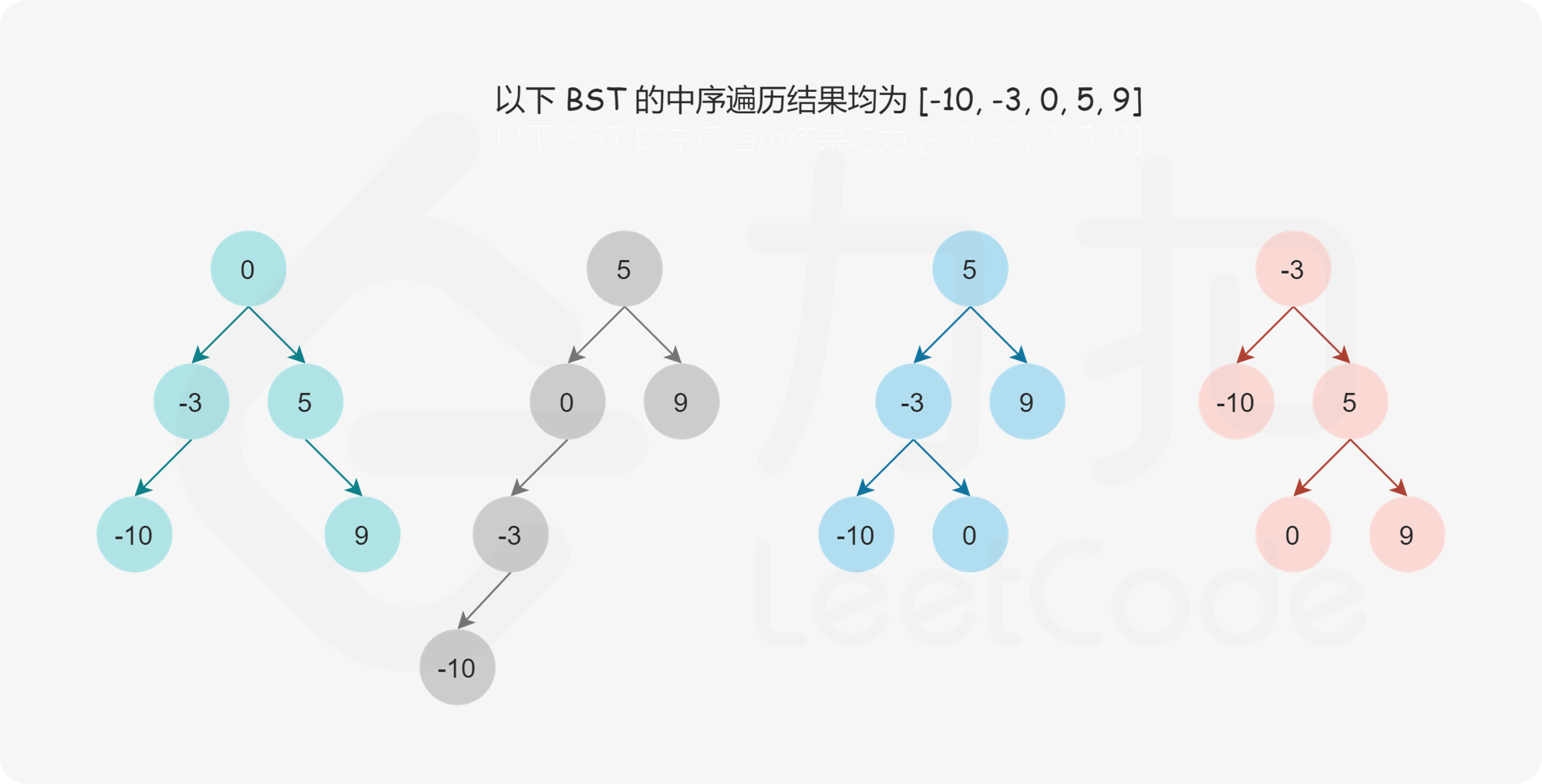
  如果增加一个限制条件，即要求二叉搜索树的高度平衡，是否可以唯一地确定二叉搜索树？答案仍然是否定的。

  

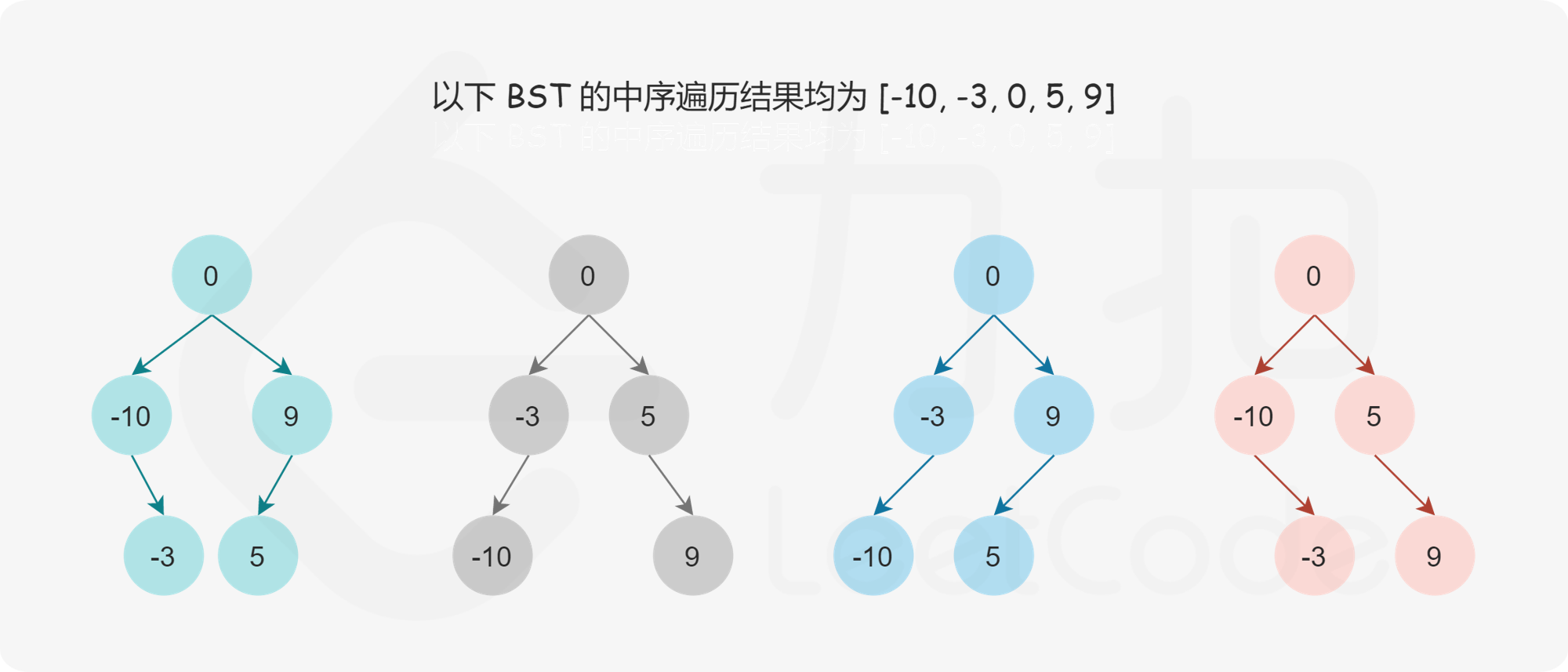
  直观地看，我们可以选择中间数字作为二叉搜索树的根节点，这样分给左右子树的数字个数相同或只相差 11，可以使得树保持平衡。如果数组长度是奇数，则根节点的选择是唯一的，如果数组长度是偶数，则可以选择中间位置左边的数字作为根节点或者选择中间位置右边的数字作为根节点，选择不同的数字作为根节点则创建的平衡二叉搜索树也是不同的。

  

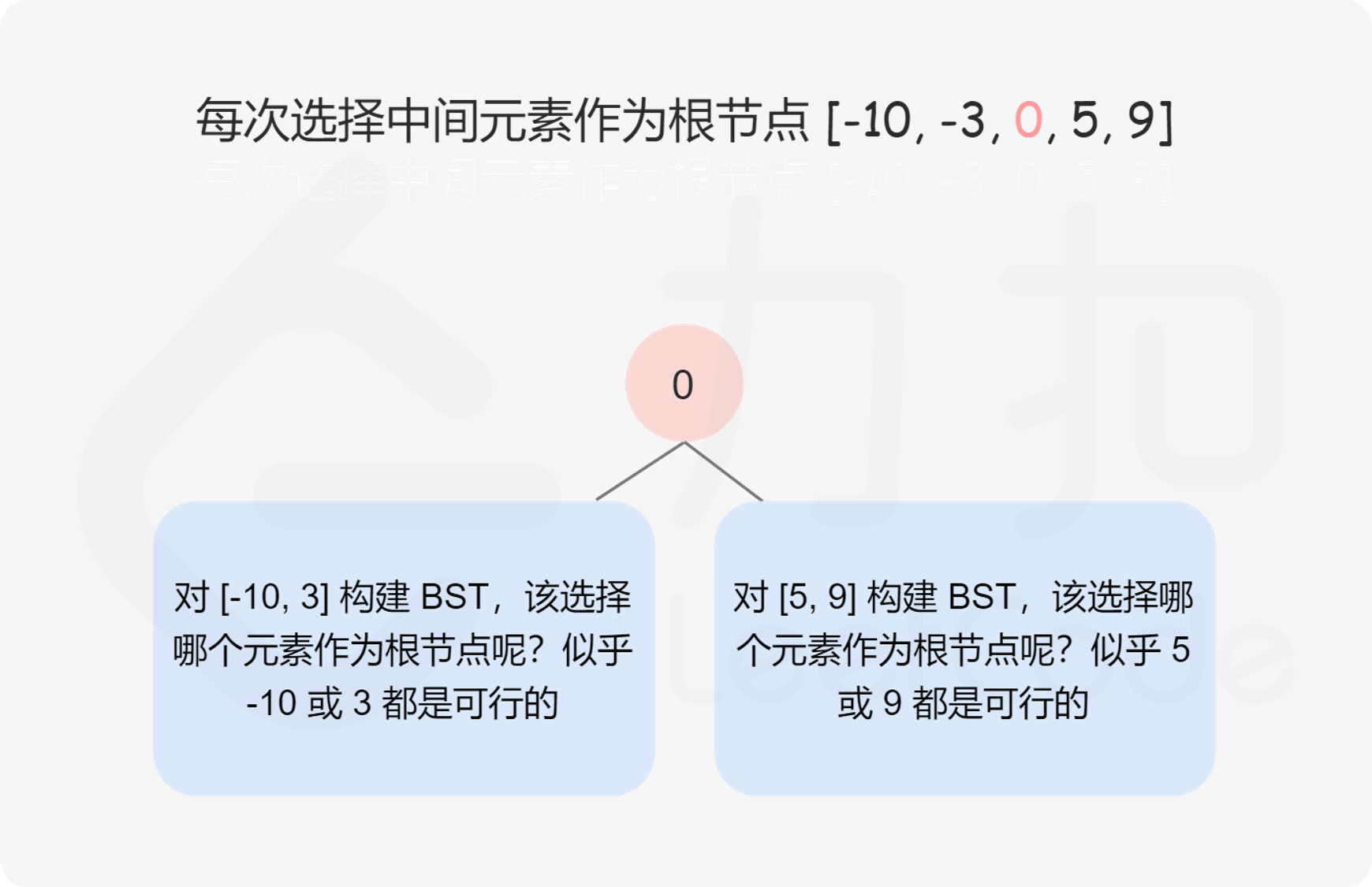
  确定平衡二叉搜索树的根节点之后，其余的数字分别位于平衡二叉搜索树的左子树和右子树中，左子树和右子树分别也是平衡二叉搜索树，因此可以通过递归的方式创建平衡二叉搜索树。

  当然，这只是我们直观的想法，为什么这么建树一定能保证是「平衡」的呢？这里可以参考「1382. 将二叉搜索树变平衡」，这两道题的构造方法完全相同，这种方法是正确的，1382 题解中给出了这个方法的正确性证明：1382 官方题解，感兴趣的同学可以戳进去参考。

  递归的基准情形是平衡二叉搜索树不包含任何数字，此时平衡二叉搜索树为空。

  在给定中序遍历序列数组的情况下，每一个子树中的数字在数组中一定是连续的，因此可以通过数组下标范围确定子树包含的数字，下标范围记为 [left,right]。对于整个中序遍历序列，下标范围从 left=0 到 right*=nums.length−1。当 left>*right 时，平衡二叉搜索树为空。

  以下三种方法中，方法一总是选择中间位置左边的数字作为根节点，方法二总是选择中间位置右边的数字作为根节点，方法三是方法一和方法二的结合，选择任意一个中间位置数字作为根节点。

  方法一：中序遍历，总是选择中间位置左边的数字作为根节点

  选择中间位置左边的数字作为根节点，则根节点的下标为 mid*=(*left+right)/2，此处的除法为整数除法。

  

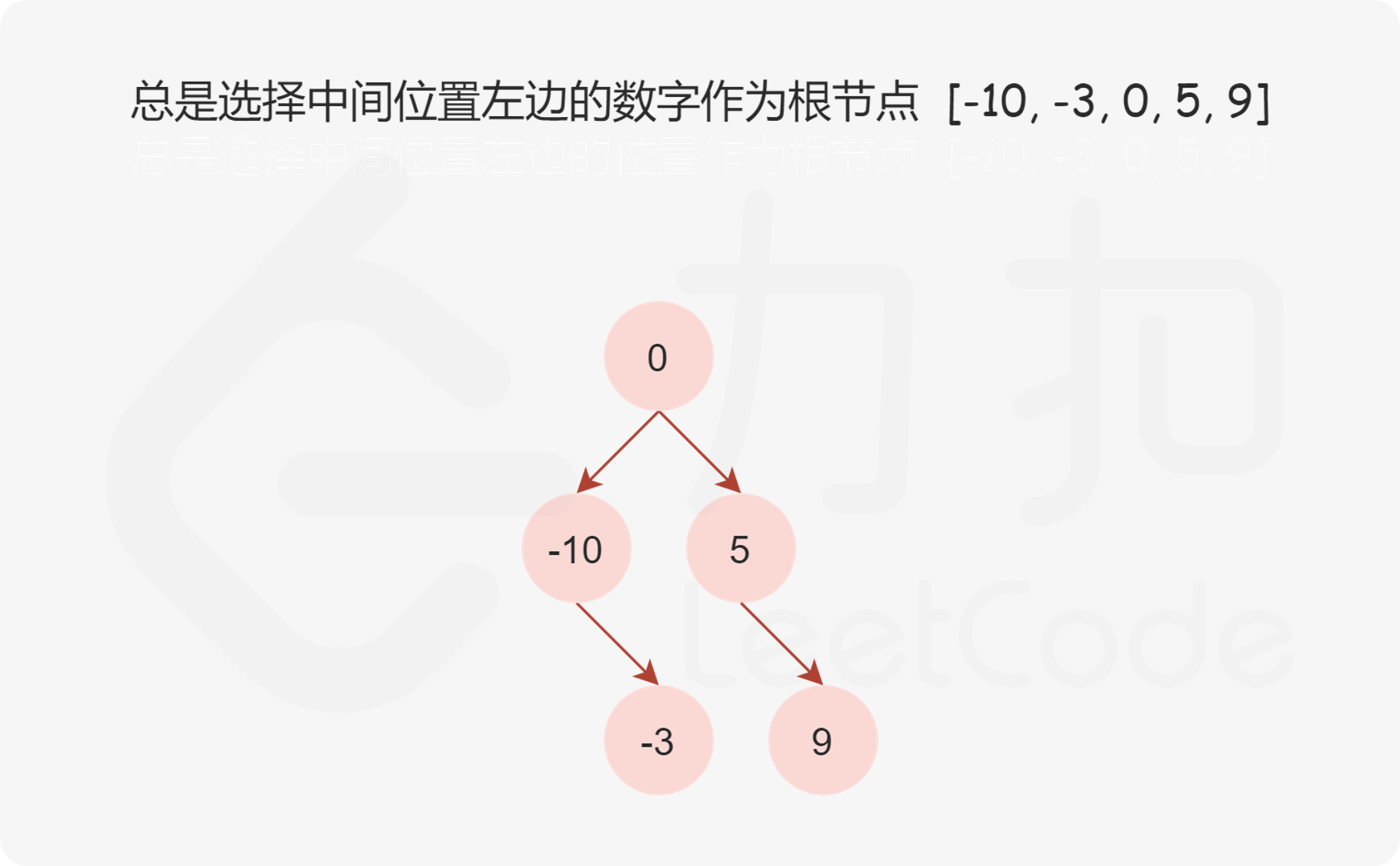
  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  class Solution { public TreeNode sortedArrayToBST(int[] nums) { return helper(nums, 0, nums.length - 1); } public TreeNode helper(int[] nums, int left, int right) { if (left > right) { return null; } // 总是选择中间位置左边的数字作为根节点 int mid = (left + right) / 2; TreeNode root = new TreeNode(nums[mid]); root.left = helper(nums, left, mid - 1); root.right = helper(nums, mid + 1, right); return root; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
  • 空间复杂度：O(log n)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(log n)。

  方法二：中序遍历，总是选择中间位置右边的数字作为根节点

  选择中间位置右边的数字作为根节点，则根节点的下标为 mid=(left+right+1)/2，此处的除法为整数除法。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  class Solution { public TreeNode sortedArrayToBST(int[] nums) { return helper(nums, 0, nums.length - 1); } public TreeNode helper(int[] nums, int left, int right) { if (left > right) { return null; } // 总是选择中间位置右边的数字作为根节点 int mid = (left + right + 1) / 2; TreeNode root = new TreeNode(nums[mid]); root.left = helper(nums, left, mid - 1); root.right = helper(nums, mid + 1, right); return root; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
  • 空间复杂度：O(log n)，其中 nn 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(log n)。

  方法三：中序遍历，选择任意一个中间位置数字作为根节点

  选择任意一个中间位置数字作为根节点，则根节点的下标为 mid=(left+right)/2 和 mid=(left+right+1)/2 两者中随机选择一个，此处的除法为整数除法。

  

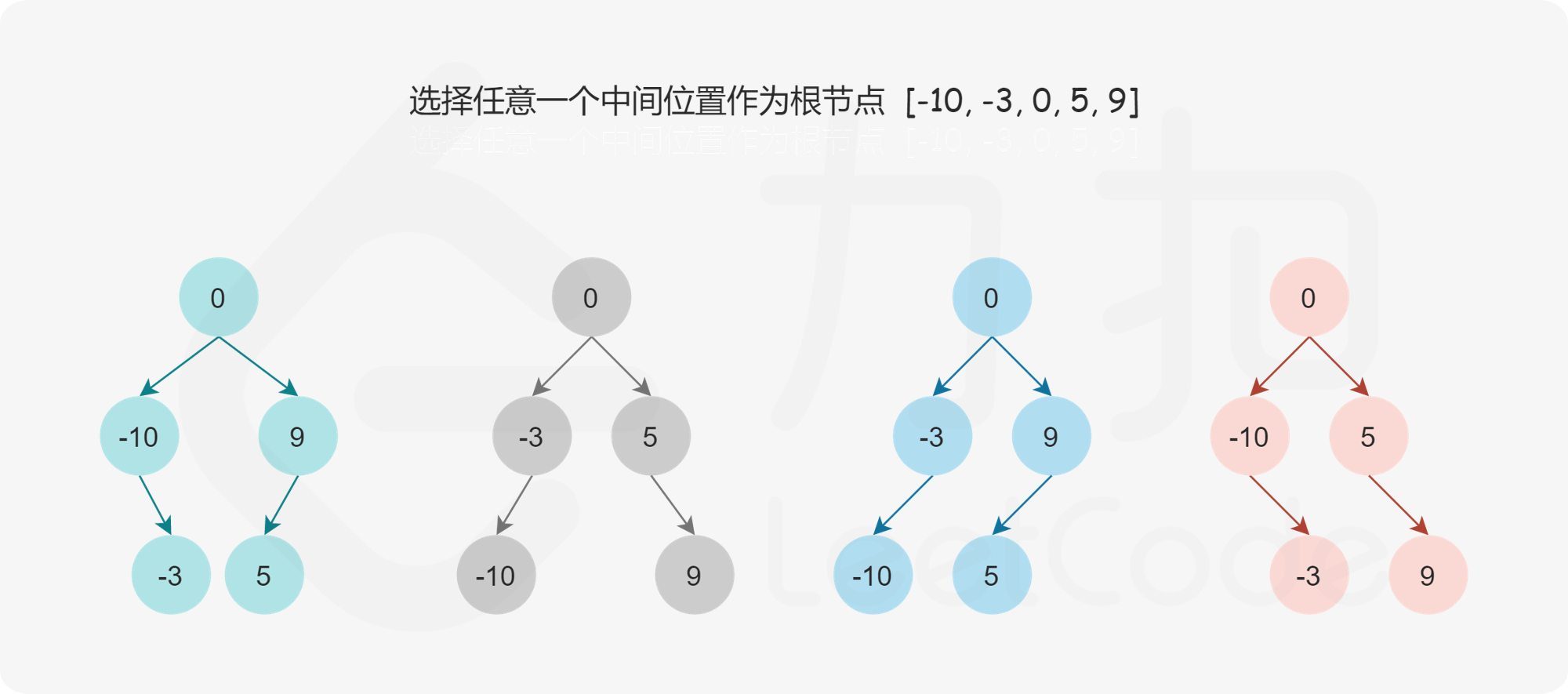
  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { Random rand = new Random(); public TreeNode sortedArrayToBST(int[] nums) { return helper(nums, 0, nums.length - 1); } public TreeNode helper(int[] nums, int left, int right) { if (left > right) { return null; } // 选择任意一个中间位置数字作为根节点 int mid = (left + right + rand.nextInt(2)) / 2; TreeNode root = new TreeNode(nums[mid]); root.left = helper(nums, left, mid - 1); root.right = helper(nums, mid + 1, right); return root; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是数组的长度。每个数字只访问一次。
  • 空间复杂度：O(log n)，其中 n 是数组的长度。空间复杂度不考虑返回值，因此空间复杂度主要取决于递归栈的深度，递归栈的深度是 O(log n)。

  day51

  235. 二叉搜索树的最近公共祖先

  • 题目

    给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

    百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

    例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

    

    示例 1:

    1 2 3

    输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8 输出: 6 解释: 节点 2 和节点 8 的最近公共祖先是 6。

    示例 2:

    1 2 3

    输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4 输出: 2 解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

    说明:

    • 所有节点的值都是唯一的。
    • p、q 为不同节点且均存在于给定的二叉搜索树中。

  • 解法

    方法一：两次遍历

    思路与算法

    注意到题目中给出的是一棵「二叉搜索树」，因此我们可以快速地找出树中的某个节点以及从根节点到该节点的路径，例如我们需要找到节点 p：

    • 我们从根节点开始遍历；
    • 如果当前节点就是 p，那么成功地找到了节点；
    • 如果当前节点的值大于 p 的值，说明 p 应该在当前节点的左子树，因此将当前节点移动到它的左子节点；
    • 如果当前节点的值小于 p 的值，说明 p 应该在当前节点的右子树，因此将当前节点移动到它的右子节点。

    对于节点 q 同理。在寻找节点的过程中，我们可以顺便记录经过的节点，这样就得到了从根节点到被寻找节点的路径。

    当我们分别得到了从根节点到 p 和 q 的路径之后，我们就可以很方便地找到它们的最近公共祖先了。显然，p 和 q 的最近公共祖先就是从根节点到它们路径上的「分岔点」，也就是最后一个相同的节点。因此，如果我们设从根节点到 p 的路径为数组 path_p，从根节点到 q 的路径为数组 path_q，那么只要找出最大的编号 i，其满足path_p[i]=path_q[i]

    那么对应的节点就是「分岔点」，即 p 和 q 的最近公共祖先就是 path_p[i]（或 path_q[i]）。

    代码

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

    class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { List<TreeNode> path_p = getPath(root, p); List<TreeNode> path_q = getPath(root, q); TreeNode ancestor = null; for (int i = 0; i < path_p.size() && i < path_q.size(); ++i) { if (path_p.get(i) == path_q.get(i)) { ancestor = path_p.get(i); } else { break; } } return ancestor; } public List<TreeNode> getPath(TreeNode root, TreeNode target) { List<TreeNode> path = new ArrayList<TreeNode>(); TreeNode node = root; while (node != target) { path.add(node); if (target.val < node.val) { node = node.left; } else { node = node.right; } } path.add(node); return path; } }

    复杂度分析

    • 时间复杂度：O(n)，其中 n 是给定的二叉搜索树中的节点个数。上述代码需要的时间与节点 p 和 q 在树中的深度线性相关，而在最坏的情况下，树呈现链式结构，p 和 q 一个是树的唯一叶子结点，一个是该叶子结点的父节点，此时时间复杂度为Θ(n)。
    • 空间复杂度：O(n)，我们需要存储根节点到 p 和 q 的路径。和上面的分析方法相同，在最坏的情况下，路径的长度为 Θ(n)，因此需要 Θ(n) 的空间。

    方法二：一次遍历

    思路与算法

    在方法一中，我们对从根节点开始，通过遍历找出到达节点 p 和 q 的路径，一共需要两次遍历。我们也可以考虑将这两个节点放在一起遍历。

    整体的遍历过程与方法一中的类似：

    • 我们从根节点开始遍历；
    • 如果当前节点的值大于 p 和 q 的值，说明 p 和 q 应该在当前节点的左子树，因此将当前节点移动到它的左子节点；
    • 如果当前节点的值小于 p 和 q 的值，说明 p 和 q 应该在当前节点的右子树，因此将当前节点移动到它的右子节点；
    • 如果当前节点的值不满足上述两条要求，那么说明当前节点就是「分岔点」。此时，p 和 q 要么在当前节点的不同的子树中，要么其中一个就是当前节点。

    可以发现，如果我们将这两个节点放在一起遍历，我们就省去了存储路径需要的空间。

    代码

    1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

    class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { TreeNode ancestor = root; while (true) { if (p.val < ancestor.val && q.val < ancestor.val) { ancestor = ancestor.left; } else if (p.val > ancestor.val && q.val > ancestor.val) { ancestor = ancestor.right; } else { break; } } return ancestor; } }

    复杂度分析

    • 时间复杂度：O(n)，其中 n 是给定的二叉搜索树中的节点个数。分析思路与方法一相同。
    • 空间复杂度：O(1)。

day51

450. 删除二叉搜索树中的节点

• 题目

  给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

  一般来说，删除节点可分为两个步骤：

  1. 首先找到需要删除的节点；
  2. 如果找到了，删除它。

  示例 1:

  

  1 2 3 4 5

  输入：root = [5,3,6,2,4,null,7], key = 3 输出：[5,4,6,2,null,null,7] 解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。

  示例 2:

  1 2 3

  输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点

  示例 3:

  1 2	输入: root = [], key = 0 输出: []

  提示:

  • 节点数的范围 [0, 104].
  • -105 <= Node.val <= 105
  • 节点值唯一
  • root 是合法的二叉搜索树
  • -105 <= key <= 105

  进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

• 解法

  方法一：递归

  思路

  二叉搜索树有以下性质：

  • 左子树的所有节点（如果有）的值均小于当前节点的值；
  • 右子树的所有节点（如果有）的值均大于当前节点的值；
  • 左子树和右子树均为二叉搜索树。

  二叉搜索树的题目往往可以用递归来解决。此题要求删除二叉树的节点，函数 deleteNode 的输入是二叉树的根节点 root 和一个整数 key，输出是删除值为 key 的节点后的二叉树，并保持二叉树的有序性。可以按照以下情况分类讨论：

  • root 为空，代表未搜索到值为 key 的节点，返回空。
  • root.val*>*key，表示值为 key 的节点可能存在于 root 的左子树中，需要递归地在 root.left 调用 deleteNode，并返回 root。
  • root.val*<*key，表示值为 key 的节点可能存在于 root 的右子树中，需要递归地在 root.right 调用 deleteNode，并返回root。
  • root.val*=*key，root即为要删除的节点。此时要做的是删除root，并将它的子树合并成一棵子树，保持有序性，并返回根节点。根据root的子树情况分成以下情况讨论：
    • root 为叶子节点，没有子树。此时可以直接将它删除，即返回空。
    • root 只有左子树，没有右子树。此时可以将它的左子树作为新的子树，返回它的左子节点。
    • root 只有右子树，没有左子树。此时可以将它的右子树作为新的子树，返回它的右子节点。
    • root 有左右子树，这时可以将 root 的后继节点（比 root 大的最小节点，即它的右子树中的最小节点，记为 successor）作为新的根节点替代 root，并将 successor 从 root 的右子树中删除，使得在保持有序性的情况下合并左右子树。 简单证明，successor 位于 root 的右子树中，因此大于 root 的所有左子节点；successor 是 root 的右子树中的最小节点，因此小于 root 的右子树中的其他节点。以上两点保持了新子树的有序性。 在代码实现上，我们可以先寻找 successor，再删除它。successor 是 root 的右子树中的最小节点，可以先找到 root 的右子节点，再不停地往左子节点寻找，直到找到一个不存在左子节点的节点，这个节点即为 successor。然后递归地在 root.right 调用 deleteNode 来删除 successor。因为 successor 没有左子节点，因此这一步递归调用不会再次步入这一种情况。然后将 successor 更新为新的 root 并返回。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  class Solution { public TreeNode deleteNode(TreeNode root, int key) { if (root == null) { return null; } if (root.val > key) { root.left = deleteNode(root.left, key); return root; } if (root.val < key) { root.right = deleteNode(root.right, key); return root; } if (root.val == key) { if (root.left == null && root.right == null) { return null; } if (root.right == null) { return root.left; } if (root.left == null) { return root.right; } TreeNode successor = root.right; while (successor.left != null) { successor = successor.left; } root.right = deleteNode(root.right, successor.val); successor.right = root.right; successor.left = root.left; return successor; } return root; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为 root 的节点个数。最差情况下，寻找和删除 successor 各需要遍历一次树。
  • 空间复杂度：O(n)，其中 n 为 root 的节点个数。递归的深度最深为 O(n)。

  方法二：迭代

  思路

  方法一的递归深度最多为 n，而大部分是由寻找值为 key 的节点贡献的，而寻找节点这一部分可以用迭代来优化。寻找并删除 successor 时，也可以用一个变量保存它的父节点，从而可以节省一步递归操作。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  class Solution { public TreeNode deleteNode(TreeNode root, int key) { TreeNode cur = root, curParent = null; while (cur != null && cur.val != key) { curParent = cur; if (cur.val > key) { cur = cur.left; } else { cur = cur.right; } } if (cur == null) { return root; } if (cur.left == null && cur.right == null) { cur = null; } else if (cur.right == null) { cur = cur.left; } else if (cur.left == null) { cur = cur.right; } else { TreeNode successor = cur.right, successorParent = cur; while (successor.left != null) { successorParent = successor; successor = successor.left; } if (successorParent.val == cur.val) { successorParent.right = successor.right; } else { successorParent.left = successor.right; } successor.right = cur.right; successor.left = cur.left; cur = successor; } if (curParent == null) { return cur; } else { if (curParent.left != null && curParent.left.val == key) { curParent.left = cur; } else { curParent.right = cur; } return root; } } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为 root 的节点个数。最差情况下，需要遍历一次树。
  • 空间复杂度：O(1)。使用的空间为常数。

day52

501. 二叉搜索树中的众数

• 题目

  给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。

  如果树中有不止一个众数，可以按 任意顺序 返回。

  假定 BST 满足如下定义：

  • 结点左子树中所含节点的值 小于等于 当前节点的值
  • 结点右子树中所含节点的值 大于等于 当前节点的值
  • 左子树和右子树都是二叉搜索树

  示例 1：

  

  1 2	输入：root = [1,null,2,2] 输出：[2]

  示例 2：

  1 2	输入：root = [0] 输出：[0]

  提示：

  • 树中节点的数目在范围 [1, 104] 内
  • -105 <= Node.val <= 105

  **进阶：**你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

• 解法

  方法一：当作普通二叉树

  先便利二叉树，然后值作为键，重复次数作为值放到一个map，之后统计这个map即可

  方法二：中序遍历

  思路与算法

  首先我们一定能想到一个最朴素的做法：因为这棵树的中序遍历是一个有序的序列，所以我们可以先获得这棵树的中序遍历，然后从扫描这个中序遍历序列，然后用一个哈希表来统计每个数字出现的个数，这样就可以找到出现次数最多的数字。但是这样做的空间复杂度显然不是 O(1) 的，原因是哈希表和保存中序遍历序列的空间代价都是 O(n)。

  首先，我们考虑在寻找出现次数最多的数时，不使用哈希表。 这个优化是基于二叉搜索树中序遍历的性质：一棵二叉搜索树的中序遍历序列是一个非递减的有序序列。例如：

  1 2 3 4 5

  1 / \ 0 2 / \ / -1 0 2

  这样一颗二叉搜索树的中序遍历序列是 {−1,0,0,1,2,2}。我们可以发现重复出现的数字一定是一个连续出现的，例如这里的 0 和 2，它们都重复出现了，并且所有的 0 都集中在一个连续的段内，所有的 2 也集中在一个连续的段内。我们可以顺序扫描中序遍历序列，用 base 记录当前的数字，用 count 记录当前数字重复的次数，用 maxCount 来维护已经扫描过的数当中出现最多的那个数字的出现次数，用 answer 数组记录出现的众数。每次扫描到一个新的元素：

  • 首先更新base和count:
    • 如果该元素和 base 相等，那么 count 自增 1；
    • 否则将 base 更新为当前数字，count 复位为 1。
  • 然后更新maxCount：
    • 如果 count = maxCount，那么说明当前的这个数字（base）出现的次数等于当前众数出现的次数，将 base 加入 answer 数组；
    • 如果 count*>*maxCount，那么说明当前的这个数字（base）出现的次数大于当前众数出现的次数，因此，我们需要将 maxCount 更新为 count，清空 answer 数组后将 base 加入 answer 数组。

  我们可以把这个过程写成一个 update 函数。这样我们在寻找出现次数最多的数字的时候就可以省去一个哈希表带来的空间消耗。

  然后，我们考虑不存储这个中序遍历序列。 如果我们在递归进行中序遍历的过程中，访问当了某个点的时候直接使用上面的 update 函数，就可以省去中序遍历序列的空间，代码如下。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  class Solution { List<Integer> answer = new ArrayList<Integer>(); int base, count, maxCount; public int[] findMode(TreeNode root) { dfs(root); int[] mode = new int[answer.size()]; for (int i = 0; i < answer.size(); ++i) { mode[i] = answer.get(i); } return mode; } public void dfs(TreeNode o) { if (o == null) { return; } dfs(o.left); update(o.val); dfs(o.right); } public void update(int x) { if (x == base) { ++count; } else { count = 1; base = x; } if (count == maxCount) { answer.add(base); } if (count > maxCount) { maxCount = count; answer.clear(); answer.add(base); } } }

  复杂度分析

  • 时间复杂度：O(n)。即遍历这棵树的复杂度。
  • 空间复杂度：O(n)。即递归的栈空间的空间代价。

  方法三：Morris 中序遍历

  思路与算法

  接着上面的思路，我们用 Morris 中序遍历的方法把中序遍历的空间复杂度优化到 O(1)。 我们在中序遍历的时候，一定先遍历左子树，然后遍历当前节点，最后遍历右子树。在常规方法中，我们用递归回溯或者是栈来保证遍历完左子树可以再回到当前节点，但这需要我们付出额外的空间代价。我们需要用一种巧妙地方法可以在 O(1) 的空间下，遍历完左子树可以再回到当前节点。我们希望当前的节点在遍历完当前点的前驱之后被遍历，我们可以考虑修改它的前驱节点的 right 指针。当前节点的前驱节点的 right 指针可能本来就指向当前节点（前驱是当前节点的父节点），也可能是当前节点左子树最右下的节点。如果是后者，我们希望遍历完这个前驱节点之后再回到当前节点，可以将它的 right 指针指向当前节点。

  Morris 中序遍历的一个重要步骤就是寻找当前节点的前驱节点，并且 Morris 中序遍历寻找下一个点始终是通过转移到 right 指针指向的位置来完成的。

  • 如果当前节点没有左子树，则遍历这个点，然后跳转到当前节点的右子树。
  • 如果当前节点有左子树，那么它的前驱节点一定在左子树上，我们可以在左子树上一直向右行走，找到当前点的前驱节点。
    • 如果前驱节点没有右子树，就将前驱节点的 right 指针指向当前节点。这一步是为了在遍历完前驱节点后能找到前驱节点的后继，也就是当前节点。
    • 如果前驱节点的右子树为当前节点，说明前驱节点已经被遍历过并被修改了 right 指针，这个时候我们重新将前驱的右孩子设置为空，遍历当前的点，然后跳转到当前节点的右子树。

  因此我们可以得到这样的代码框架：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  TreeNode *cur = root, *pre = nullptr; while (cur) { if (!cur->left) { // ...遍历 cur cur = cur->right; continue; } pre = cur->left; while (pre->right && pre->right != cur) { pre = pre->right; } if (!pre->right) { pre->right = cur; cur = cur->left; } else { pre->right = nullptr; // ...遍历 cur cur = cur->right; } }

  最后我们将 ...遍历 cur 替换成之前的 update 函数即可。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

  class Solution { int base, count, maxCount; List<Integer> answer = new ArrayList<Integer>(); public int[] findMode(TreeNode root) { TreeNode cur = root, pre = null; while (cur != null) { if (cur.left == null) { update(cur.val); cur = cur.right; continue; } pre = cur.left; while (pre.right != null && pre.right != cur) { pre = pre.right; } if (pre.right == null) { pre.right = cur; cur = cur.left; } else { pre.right = null; update(cur.val); cur = cur.right; } } int[] mode = new int[answer.size()]; for (int i = 0; i < answer.size(); ++i) { mode[i] = answer.get(i); } return mode; } public void update(int x) { if (x == base) { ++count; } else { count = 1; base = x; } if (count == maxCount) { answer.add(base); } if (count > maxCount) { maxCount = count; answer.clear(); answer.add(base); } } }

  复杂度分析

  • 时间复杂度：O(n)。每个点被访问的次数不会超过两次，故这里的时间复杂度是 O(n)。
  • 空间复杂度：O(1)。使用临时空间的大小和输入规模无关。

day53

530. 二叉搜索树的最小绝对差

• 题目

  给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

  差值是一个正数，其数值等于两值之差的绝对值。

  示例 1：

  

  1 2	输入：root = [4,2,6,1,3] 输出：1

  示例 2：

  

  1 2	输入：root = [1,0,48,null,null,12,49] 输出：1

  提示：

  • 树中节点的数目范围是 [2, 104]
  • 0 <= Node.val <= 105

  **注意：**本题与 783 https://leetcode-cn.com/problems/minimum-distance-between-bst-nodes/ 相同

• 解法

  方法一：中序遍历

  思路与算法

  考虑对升序数组 aa 求任意两个元素之差的绝对值的最小值，答案一定为相邻两个元素之差的最小值，即 $$ \textit{ans}=\min_{i=0}^{n-2}\left{a[i+1]-a[i]\right} $$ 其中 n 为数组 a 的长度。其他任意间隔距离大于等于 2 的下标对 (i,j) 的元素之差一定大于下标对 (i,i+1) 的元素之差，故不需要再被考虑。

  回到本题，本题要求二叉搜索树任意两节点差的绝对值的最小值，而我们知道二叉搜索树有个性质为二叉搜索树中序遍历得到的值序列是递增有序的，因此我们只要得到中序遍历后的值序列即能用上文提及的方法来解决。

  朴素的方法是经过一次中序遍历将值保存在一个数组中再进行遍历求解，我们也可以在中序遍历的过程中用 pre 变量保存前驱节点的值，这样即能边遍历边更新答案，不再需要显式创建数组来保存，需要注意的是 pre 的初始值需要设置成任意负数标记开头，下文代码中设置为 -1−1。

  二叉树的中序遍历有多种方式，包括递归、栈、Morris 遍历等，读者可选择自己最擅长的来实现。下文代码提供最普遍的递归方法来实现，其他遍历方法的介绍可以详细看「94. 二叉树的中序遍历的官方题解」，这里不再赘述。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  class Solution { int pre; int ans; public int getMinimumDifference(TreeNode root) { ans = Integer.MAX_VALUE; pre = -1; dfs(root); return ans; } public void dfs(TreeNode root) { if (root == null) { return; } dfs(root.left); if (pre == -1) { pre = root.val; } else { ans = Math.min(ans, root.val - pre); pre = root.val; } dfs(root.right); } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉搜索树节点的个数。每个节点在中序遍历中都会被访问一次且只会被访问一次，因此总时间复杂度为 O(n)。
  • 空间复杂度：O(n)。递归函数的空间复杂度取决于递归的栈深度，而栈深度在二叉搜索树为一条链的情况下会达到 O(n) 级别。

day54

538. 把二叉搜索树转换为累加树

• 题目

  给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

  提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键 小于 节点键的节点。
  • 节点的右子树仅包含键 大于 节点键的节点。
  • 左右子树也必须是二叉搜索树。

  **注意：**本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

  示例 1：

  

  1 2	输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

  示例 2：

  1 2	输入：root = [0,null,1] 输出：[1,null,1]

  示例 3：

  1 2	输入：root = [1,0,2] 输出：[3,3,2]

  示例 4：

  1 2	输入：root = [3,2,4,1] 输出：[7,9,4,10]

  提示：

  • 树中的节点数介于 0 和 104 之间。
  • 每个节点的值介于 -104 和 104 之间。
  • 树中的所有值 互不相同 。
  • 给定的树为二叉搜索树。

• 解法

  前言

  二叉搜索树是一棵空树，或者是具有下列性质的二叉树：

  1. 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；
  2. 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值；
  3. 它的左、右子树也分别为二叉搜索树。

  由这样的性质我们可以发现，二叉搜索树的中序遍历是一个单调递增的有序序列。如果我们反序地中序遍历该二叉搜索树，即可得到一个单调递减的有序序列。

  方法一：反序中序遍历

  思路及算法

  本题中要求我们将每个节点的值修改为原来的节点值加上所有大于它的节点值之和。这样我们只需要反序中序遍历该二叉搜索树，记录过程中的节点值之和，并不断更新当前遍历到的节点的节点值，即可得到题目要求的累加树。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13

  class Solution { int sum = 0; public TreeNode convertBST(TreeNode root) { if (root != null) { convertBST(root.right); sum += root.val; root.val = sum; convertBST(root.left); } return root; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。每一个节点恰好被遍历一次。
  • 空间复杂度：O(n)，为递归过程中栈的开销，平均情况下为 O(log n)，最坏情况下树呈现链状，为 O(n)。

  方法二：Morris 遍历

  思路及算法

  有一种巧妙的方法可以在线性时间内，只占用常数空间来实现中序遍历。这种方法由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出，因此被称为 Morris 遍历。

  Morris 遍历的核心思想是利用树的大量空闲指针，实现空间开销的极限缩减。其反序中序遍历规则总结如下：

  1. 如果当前节点的右子节点为空，处理当前节点，并遍历当前节点的左子节点；
  2. 如果当前节点的右子节点不为空，找到当前节点右子树的最左节点（该节点为当前节点中序遍历的前驱节点）；
     • 如果最左节点的左指针为空，将最左节点的左指针指向当前节点，遍历当前节点的右子节点；
     • 如果最左节点的左指针不为空，将最左节点的左指针重新置为空（恢复树的原状），处理当前节点，并将当前节点置为其左节点；
  3. 重复步骤 1 和步骤 2，直到遍历结束。

  这样我们利用 Morris 遍历的方法，反序中序遍历该二叉搜索树，即可实现线性时间与常数空间的遍历。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35

  class Solution { public TreeNode convertBST(TreeNode root) { int sum = 0; TreeNode node = root; while (node != null) { if (node.right == null) { sum += node.val; node.val = sum; node = node.left; } else { TreeNode succ = getSuccessor(node); if (succ.left == null) { succ.left = node; node = node.right; } else { succ.left = null; sum += node.val; node.val = sum; node = node.left; } } } return root; } public TreeNode getSuccessor(TreeNode node) { TreeNode succ = node.right; while (succ.left != null && succ.left != node) { succ = succ.left; } return succ; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉搜索树的节点数。没有左子树的节点只被访问一次，有左子树的节点被访问两次。
  • 空间复杂度：O(1)。只操作已经存在的指针（树的空闲指针），因此只需要常数的额外空间。

day55

669. 修剪二叉搜索树

• 题目

  给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

  所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

  示例 1：

  

  1 2	输入：root = [1,0,2], low = 1, high = 2 输出：[1,null,2]

  示例 2：

  

  1 2	输入：root = [3,0,4,null,2,null,null,1], low = 1, high = 3 输出：[3,2,null,1]

  提示：

  • 树中节点数在范围 [1, 104] 内
  • 0 <= Node.val <= 104
  • 树中每个节点的值都是 唯一 的
  • 题目数据保证输入是一棵有效的二叉搜索树
  • 0 <= low <= high <= 104

• 解法

  方法一：递归

  对根结点 root 进行深度优先遍历。对于当前访问的结点，如果结点为空结点，直接返回空结点；如果结点的值小于 low，那么说明该结点及它的左子树都不符合要求，我们返回对它的右结点进行修剪后的结果；如果结点的值大于 high，那么说明该结点及它的右子树都不符合要求，我们返回对它的左子树进行修剪后的结果；如果结点的值位于区间 [low,high]，我们将结点的左结点设为对它的左子树修剪后的结果，右结点设为对它的右子树进行修剪后的结果。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public TreeNode trimBST(TreeNode root, int low, int high) { if (root == null) { return null; } if (root.val < low) { return trimBST(root.right, low, high); } else if (root.val > high) { return trimBST(root.left, low, high); } else { root.left = trimBST(root.left, low, high); root.right = trimBST(root.right, low, high); return root; } } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉树的结点数目。
  • 空间复杂度：O(n)。递归栈最坏情况下需要 O(n) 的空间。

  方法二：迭代

  如果一个结点 node 符合要求，即它的值位于区间 [low, high]，那么它的左子树与右子树应该如何修剪？

  我们先讨论左子树的修剪：

  • node 的左结点为空结点：不需要修剪
  • node 的左结点非空：
    • 如果它的左结点 left 的值小于 low，那么 left 以及 left 的左子树都不符合要求，我们将 node 的左结点设为 left 的右结点，然后再重新对 node 的左子树进行修剪。
    • 如果它的左结点 left 的值大于等于 low，又因为 node 的值已经符合要求，所以 left 的右子树一定符合要求。基于此，我们只需要对 left 的左子树进行修剪。我们令 node 等于 left ，然后再重新对 node 的左子树进行修剪。

  以上过程可以迭代处理。对于右子树的修剪同理。

  我们对根结点进行判断，如果根结点不符合要求，我们将根结点设为对应的左结点或右结点，直到根结点符合要求，然后将根结点作为符合要求的结点，依次修剪它的左子树与右子树。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

  class Solution { public TreeNode trimBST(TreeNode root, int low, int high) { while (root != null && (root.val < low || root.val > high)) { if (root.val < low) { root = root.right; } else { root = root.left; } } if (root == null) { return null; } for (TreeNode node = root; node.left != null; ) { if (node.left.val < low) { node.left = node.left.right; } else { node = node.left; } } for (TreeNode node = root; node.right != null; ) { if (node.right.val > high) { node.right = node.right.left; } else { node = node.right; } } return root; } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 为二叉树的结点数目。最多访问 n 个结点。
  • 空间复杂度：O(1)。

day56

701. 二叉搜索树中的插入操作

• 题目

  给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

  注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

  示例 1：

  

  1 2 3

  输入：root = [4,2,7,1,3], val = 5 输出：[4,2,7,1,3,5] 解释：另一个满足题目要求可以通过的树是：

  示例 2：

  1 2	输入：root = [40,20,60,10,30,50,70], val = 25 输出：[40,20,60,10,30,50,70,null,null,25]

  示例 3：

  1 2	输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5 输出：[4,2,7,1,3,5]

  提示：

  • 树中的节点数将在 [0, 104]的范围内。
  • -108 <= Node.val <= 108
  • 所有值 Node.val 是 独一无二 的。
  • -108 <= val <= 108
  • 保证 val 在原始BST中不存在。

• 解法

  方法一：模拟

  思路与算法

  首先回顾二叉搜索树的性质：对于任意节点 root 而言，左子树（如果存在）上所有节点的值均小于 root.val，右子树（如果存在）上所有节点的值均大于 root.val，且它们都是二叉搜索树。

  因此，当将 val 插入到以 root 为根的子树上时，根据 val 与 root.val 的大小关系，就可以确定要将 val 插入到哪个子树中。

  • 如果该子树不为空，则问题转化成了将 val 插入到对应子树上。
  • 否则，在此处新建一个以 val 为值的节点，并链接到其父节点 root 上。

  代码

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  class Solution { public TreeNode insertIntoBST(TreeNode root, int val) { if (root == null) { return new TreeNode(val); } TreeNode pos = root; while (pos != null) { if (val < pos.val) { if (pos.left == null) { pos.left = new TreeNode(val); break; } else { pos = pos.left; } } else { if (pos.right == null) { pos.right = new TreeNode(val); break; } else { pos = pos.right; } } } return root; } }

  复杂度分析

  • 时间复杂度：O(N)，其中 N 为树中节点的数目。最坏情况下，我们需要将值插入到树的最深的叶子结点上，而叶子节点最深为 O(N)。
  • 空间复杂度：O(1)。我们只使用了常数大小的空间。

  方法二：递归、

  我们知道二叉搜索树插入新的节点时，如果还要满足BST性质，那么还有一种简单得思路：直接遍历到何时得叶子节点，插入到叶子节点末尾即可。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  class Solution { TreeNode parent = null; int flag = 0; // 二叉排序树插入节点，一定可以插入到叶子节点 public TreeNode insertIntoBST(TreeNode root, int val) { if(root==null) { if(flag == -1){ return new TreeNode(val); }else{ return new TreeNode(val); } } if(val>root.val){ parent = root; flag = 1; root.right = insertIntoBST(root.right,val); } else if(val<root.val){ parent = root; flag = -1; root.left = insertIntoBST(root.left,val); } return root; } }

day57

110. 平衡二叉树

• 题目

  给定一个二叉树，判断它是否是高度平衡的二叉树。

  本题中，一棵高度平衡二叉树定义为：

  一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

  示例 1：

  

  1 2	输入：root = [3,9,20,null,null,15,7] 输出：true

  示例 2：

  

  1 2	输入：root = [1,2,2,3,3,null,null,4,4] 输出：false

  示例 3：

  1 2	输入：root = [] 输出：true

  提示：

  • 树中的节点数在范围 [0, 5000] 内
  • -104 <= Node.val <= 104

• 解法

  前言

  这道题中的平衡二叉树的定义是：二叉树的每个节点的左右子树的高度差的绝对值不超过 1，则二叉树是平衡二叉树。根据定义，一棵二叉树是平衡二叉树，当且仅当其所有子树也都是平衡二叉树，因此可以使用递归的方式判断二叉树是不是平衡二叉树，递归的顺序可以是自顶向下或者自底向上。

  方法一：自顶向下的递归

  定义函数 height，用于计算二叉树中的任意一个节点 p 的高度： $$ \texttt{height}(p) = \begin{cases} 0 & p \text{ 是空节点}\ \max(\texttt{height}(p.\textit{left}), \texttt{height}(p.\textit{right}))+1 & p \text{ 是非空节点} \end{cases} $$ 有了计算节点高度的函数，即可判断二叉树是否平衡。具体做法类似于二叉树的前序遍历，即对于当前遍历到的节点，首先计算左右子树的高度，如果左右子树的高度差是否不超过 1，再分别递归地遍历左右子节点，并判断左子树和右子树是否平衡。这是一个自顶向下的递归的过程。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  class Solution { public boolean isBalanced(TreeNode root) { if (root == null) { return true; } else { return Math.abs(height(root.left) - height(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right); } } public int height(TreeNode root) { if (root == null) { return 0; } else { return Math.max(height(root.left), height(root.right)) + 1; } } }

  复杂度分析

  • 时间复杂度：O(n^2)，其中 n 是二叉树中的节点个数。 最坏情况下，二叉树是满二叉树，需要遍历二叉树中的所有节点，时间复杂度是 O(n)。 对于节点 p，如果它的高度是 d，则 height(p) 最多会被调用 d 次（即遍历到它的每一个祖先节点时）。对于平均的情况，一棵树的高度 h 满足 O(h)=O(logn)，因为 d≤h，所以总时间复杂度为 O(nlog n)。对于最坏的情况，二叉树形成链式结构，高度为 O(n)，此时总时间复杂度为 O(n^2)。
  • 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。

  方法二：自底向上的递归

  方法一由于是自顶向下递归，因此对于同一个节点，函数 height 会被重复调用，导致时间复杂度较高。如果使用自底向上的做法，则对于每个节点，函数 height 只会被调用一次。

  自底向上递归的做法类似于后序遍历，对于当前遍历到的节点，先递归地判断其左右子树是否平衡，再判断以当前节点为根的子树是否平衡。如果一棵子树是平衡的，则返回其高度（高度一定是非负整数），否则返回 -1。如果存在一棵子树不平衡，则整个二叉树一定不平衡。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public boolean isBalanced(TreeNode root) { return height(root) >= 0; } public int height(TreeNode root) { if (root == null) { return 0; } int leftHeight = height(root.left); int rightHeight = height(root.right); if (leftHeight == -1 || rightHeight == -1 || Math.abs(leftHeight - rightHeight) > 1) { return -1; } else { return Math.max(leftHeight, rightHeight) + 1; } } }

  复杂度分析

  • 时间复杂度：O(n)，其中 n 是二叉树中的节点个数。使用自底向上的递归，每个节点的计算高度和判断是否平衡都只需要处理一次，最坏情况下需要遍历二叉树中的所有节点，因此时间复杂度是 O(n)。
  • 空间复杂度：O(n)，其中 n 是二叉树中的节点个数。空间复杂度主要取决于递归调用的层数，递归调用的层数不会超过 n。

day58

1382. 将二叉搜索树变平衡

• 题目

  给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法，请你返回任意一种。

  如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

  示例 1：

  

  1 2 3

  输入：root = [1,null,2,null,3,null,4,null,null] 输出：[2,1,3,null,null,null,4] 解释：这不是唯一的正确答案，[3,1,4,null,2,null,null] 也是一个可行的构造方案。

  示例 2：

  

  1 2	输入: root = [2,1,3] 输出: [2,1,3]

  提示：

  • 树节点的数目在 [1, 104] 范围内。
  • 1 <= Node.val <= 105

• 解法

  • 贪心构造

day59

28. 找出字符串中第一个匹配项的下标

• 题目

  给你两个字符串 haystack 和 needle ，请你在 haystack 字符串中找出 needle 字符串的第一个匹配项的下标（下标从 0 开始）。如果 needle 不是 haystack 的一部分，则返回 -1 。

  示例 1：

  1 2 3 4

  输入：haystack = "sadbutsad", needle = "sad" 输出：0 解释："sad" 在下标 0 和 6 处匹配。 第一个匹配项的下标是 0 ，所以返回 0 。

  示例 2：

  1 2 3

  输入：haystack = "leetcode", needle = "leeto" 输出：-1 解释："leeto" 没有在 "leetcode" 中出现，所以返回 -1 。

  提示：

  • 1 <= haystack.length, needle.length <= 104
  • haystack 和 needle 仅由小写英文字符组成

• 解法

  KMP

day60

459. 重复的子字符串

• 题目

  给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成。

  示例 1:

  1 2 3

  输入: s = "abab" 输出: true 解释: 可由子串 "ab" 重复两次构成。

  示例 2:

  1 2	输入: s = "aba" 输出: false

  示例 3:

  1 2 3

  输入: s = "abcabcabcabc" 输出: true 解释: 可由子串 "abc" 重复四次构成。 (或子串 "abcabc" 重复两次构成。)

  提示：

  • 1 <= s.length <= 104
  • s 由小写英文字母组成

• 解法

  https://leetcode.cn/problems/repeated-substring-pattern/solution/zhong-fu-de-zi-zi-fu-chuan-by-leetcode-solution/

day61

50. Pow(x, n)

• 题目

  实现 pow(x, n) ，即计算 x 的整数 n 次幂函数（即，xn ）。

  示例 1：

  1 2	输入：x = 2.00000, n = 10 输出：1024.00000

  示例 2：

  1 2	输入：x = 2.10000, n = 3 输出：9.26100

  示例 3：

  1 2 3

  输入：x = 2.00000, n = -2 输出：0.25000 解释：2-2 = 1/22 = 1/4 = 0.25

  提示：

  • -100.0 < x < 100.0
  • -231 <= n <= 231-1
  • -104 <= xn <= 104

• 解法

  使用暴力迭代和暴力递归均会爆栈或超时

  • 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

    // 递归求解爆栈 public double myPow(double x, int n) { if(n==0) return 1.0; else if(n>0) return myPow(x,n-1)*x; else return myPow(x,n+1)*(1.0/x); } // 迭代超时 public double myPow(double x, int n) { if(n==0) return 1.0; else if(n>0) { double r=x; for(int i=0;i<n-1;i++){ r=r*x; } return r; }else { double r=(1.0/x); for(int i=0;i<-n-1;i++){ r =r*(1.0/x); } return r; } }

  方法一：快速幂+递归

  方法二：快速幂+迭代

  https://leetcode.cn/problems/powx-n/solution/powx-n-by-leetcode-solution/

day62

33. 搜索旋转排序数组

• 题目

  整数数组 nums 按升序排列，数组中的值 互不相同 。

  在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

  给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

  你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

  示例 1：

  1 2	输入：nums = [4,5,6,7,0,1,2], target = 0 输出：4

  示例 2：

  1 2	输入：nums = [4,5,6,7,0,1,2], target = 3 输出：-1

  示例 3：

  1 2	输入：nums = [1], target = 0 输出：-1

  提示：

  • 1 <= nums.length <= 5000
  • -104 <= nums[i] <= 104
  • nums 中的每个值都 独一无二
  • 题目数据保证 nums 在预先未知的某个下标上进行了旋转
  • -104 <= target <= 104

• 解法

  https://leetcode.cn/problems/search-in-rotated-sorted-array/solution/sou-suo-xuan-zhuan-pai-xu-shu-zu-by-leetcode-solut/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  func search(nums []int, target int) int { l:=0 r:=len(nums)-1 mid :=0 for l<=r { mid = (r-l)/2+l if nums[mid] == target { return mid } if nums[mid]<nums[0]{// 右边有序 if target<=nums[r]&&target>nums[mid]{ l = mid + 1 }else{ r = mid - 1 } }else{// 左边有序 if target>=nums[l]&&target<nums[mid]{ r = mid - 1 }else{ l = mid + 1 } } } return -1 }

day63

34. 在排序数组中查找元素的第一个和最后一个位置

• 题目

  给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

  如果数组中不存在目标值 target，返回 [-1, -1]。

  你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

  示例 1：

  1 2	输入：nums = [5,7,7,8,8,10], target = 8 输出：[3,4]

  示例 2：

  1 2	输入：nums = [5,7,7,8,8,10], target = 6 输出：[-1,-1]

  示例 3：

  1 2	输入：nums = [], target = 0 输出：[-1,-1]

  提示：

  • 0 <= nums.length <= 105
  • -109 <= nums[i] <= 109
  • nums 是一个非递减数组
  • -109 <= target <= 109

• 解法

  1. 官方题解

  2. 二分+暴力

     先二分找数，找到之后再两边扩展。

     问题：如果查找的数组重复度很高，而且刚好是target的重复，算法逐渐退化到O(n).

     1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

     func searchRange(nums []int, target int) []int { ans:=[]int{-1,-1} idx:=-1 l:=0 r:=len(nums)-1 mid:=0 for l<=r{ mid = (r-l)/2+l if nums[mid]==target{ idx = mid break }else if nums[mid]>target{ r = mid - 1 }else{ l = mid + 1 } } if idx!=-1{ l=idx r=idx for l>=0&&nums[l]==target { l-- } l++ for r<len(nums)&&nums[r]==target { r++ } r-- ans[0] = l ans[1] = r } return ans }

  3. 二分+二分

     针对问题二再进行优化：二分都是找到索引最小的那个值。第一次二分找target，第二次二分找target+1的索引再-1

     1 2 3 4 5 6 7 8

     func searchRange(nums []int, target int) []int { leftmost := sort.SearchInts(nums, target) if leftmost == len(nums) || nums[leftmost] != target { return []int{-1, -1} } rightmost := sort.SearchInts(nums, target + 1) - 1 return []int{leftmost, rightmost} }

day64

81. 搜索旋转排序数组 II

• 题目

  已知存在一个按非降序排列的整数数组 nums ，数组中的值不必互不相同。

  在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转 ，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

  给你 旋转后 的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

  你必须尽可能减少整个操作步骤。

  示例 1：

  1 2	输入：nums = [2,5,6,0,0,1,2], target = 0 输出：true

  示例 2：

  1 2	输入：nums = [2,5,6,0,0,1,2], target = 3 输出：false

  提示：

  • 1 <= nums.length <= 5000
  • -104 <= nums[i] <= 104
  • 题目数据保证 nums 在预先未知的某个下标上进行了旋转
  • -104 <= target <= 104

  进阶：

  • 这是 搜索旋转排序数组 的延伸题目，本题中的 nums 可能包含重复元素。
  • 这会影响到程序的时间复杂度吗？会有怎样的影响，为什么？

• 解法

  https://leetcode.cn/problems/search-in-rotated-sorted-array-ii/solution/sou-suo-xuan-zhuan-pai-xu-shu-zu-ii-by-l-0nmp/

day65

153. 寻找旋转排序数组中的最小值

• 题目

  已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次 旋转 后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：

  • 若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
  • 若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]

  注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

  给你一个元素值 互不相同 的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。

  你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

  示例 1：

  1 2 3

  输入：nums = [3,4,5,1,2] 输出：1 解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

  示例 2：

  1 2 3

  输入：nums = [4,5,6,7,0,1,2] 输出：0 解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

  示例 3：

  1 2 3

  输入：nums = [11,13,15,17] 输出：11 解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

  提示：

  • n == nums.length
  • 1 <= n <= 5000
  • -5000 <= nums[i] <= 5000
  • nums 中的所有整数 互不相同
  • nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

• 解法

  Leecode官方题解

day66

11. 盛最多水的容器

• 题目

  给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

  找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

  返回容器可以储存的最大水量。

  **说明：**你不能倾斜容器。

  示例 1：

  

  1 2 3

  输入：[1,8,6,2,5,4,8,3,7] 输出：49 解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

  示例 2：

  1 2	输入：height = [1,1] 输出：1

  提示：

  • n == height.length
  • 2 <= n <= 105
  • 0 <= height[i] <= 104

• 解法

  双指针解法

day67

45. 跳跃游戏 II

• 题目

  给你一个非负整数数组 nums ，你最初位于数组的第一个位置。

  数组中的每个元素代表你在该位置可以跳跃的最大长度。

  你的目标是使用最少的跳跃次数到达数组的最后一个位置。

  假设你总是可以到达数组的最后一个位置。

  示例 1:

  1 2 3 4

  输入: nums = [2,3,1,1,4] 输出: 2 解释: 跳到最后一个位置的最小跳跃数是 2。 从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

  示例 2:

  1 2	输入: nums = [2,3,0,1,4] 输出: 2

  提示:

  • 1 <= nums.length <= 104
  • 0 <= nums[i] <= 1000

• 解法

  两种贪心策略解决：一种是反向查找出发位置；另一种是正向查找可达到的最大位置。

  Leecode官方题解

day68

53. 最大子数组和

• 题目

  给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

  子数组 是数组中的一个连续部分。

  示例 1：

  1 2 3

  输入：nums = [-2,1,-3,4,-1,2,1,-5,4] 输出：6 解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

  示例 2：

  1 2	输入：nums = [1] 输出：1

  示例 3：

  1 2	输入：nums = [5,4,-1,7,8] 输出：23

  提示：

  • 1 <= nums.length <= 105
  • -104 <= nums[i] <= 104

  **进阶：**如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

• 解法

  官方题解：贪心、动态规划、分治

  贪心：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  public int maxSubArray(int[] nums) { int maxSum = Integer.MIN_VALUE;//最大和 int thisSum = 0;//当前和 int len = nums.length; for(int i = 0; i < len; i++) { thisSum += nums[i]; if(maxSum < thisSum) { maxSum = thisSum; } //如果当前和小于0则归零，因为对于后面的元素来说这些是减小的。于是归零，意即从此处算开始最大和 if(thisSum < 0) { thisSum = 0; } } return maxSum; }

day69

55. 跳跃游戏

• 题目

  给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。

  数组中的每个元素代表你在该位置可以跳跃的最大长度。

  判断你是否能够到达最后一个下标。

  示例 1：

  1 2 3

  输入：nums = [2,3,1,1,4] 输出：true 解释：可以先跳 1 步，从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。

  示例 2：

  1 2 3

  输入：nums = [3,2,1,0,4] 输出：false 解释：无论怎样，总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 ， 所以永远不可能到达最后一个下标。

  提示：

  • 1 <= nums.length <= 3 * 104
  • 0 <= nums[i] <= 105

• 解法

  解法一：贪心

  官方题解

  解法一：反向遍历

  不断地从最后一个位置开始往前找能到达当前位置的索引，然后再往前找。直到找到第一个位置可以到达为止

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  func canJump(nums []int) bool { if len(nums)<=1{ return true } if nums[0] == 0 { return false } idx:=len(nums)-1 for i:=len(nums)-2;i>=0;i--{ if i+nums[i]>=idx{ // fmt.Println(idx,nums[idx]) idx = i } } return idx == 0 }

day70

56. 合并区间

• 题目

  以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

  示例 1：

  1 2 3

  输入：intervals = [[1,3],[2,6],[8,10],[15,18]] 输出：[[1,6],[8,10],[15,18]] 解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

  示例 2：

  1 2 3

  输入：intervals = [[1,4],[4,5]] 输出：[[1,5]] 解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

  提示：

  • 1 <= intervals.length <= 104
  • intervals[i].length == 2
  • 0 <= starti <= endi <= 104

• 解法

  总的来说，就是找规律

  官方题解

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

  func merge(intervals [][]int) [][]int { sort.Slice(intervals,func(i,j int) bool{ return intervals[i][0]<intervals[j][0] }) merged := [][]int{{intervals[0][0],intervals[0][1]}} for i:=1;i<len(intervals);i++{ if intervals[i][0]>merged[len(merged)-1][1]{ merged = append(merged,intervals[i]) }else if merged[len(merged)-1][1]<intervals[i][1] { merged[len(merged)-1][1] = intervals[i][1] } } return merged }

day71

121. 买卖股票的最佳时机

• 题目

  给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

  你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

  返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

  示例 1：

  1 2 3 4

  输入：[7,1,5,3,6,4] 输出：5 解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

  示例 2：

  1 2 3

  输入：prices = [7,6,4,3,1] 输出：0 解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

  提示：

  • 1 <= prices.length <= 105
  • 0 <= prices[i] <= 104

• 解法

  暴力\动态规划(记录历史最小值)

  官方题解

day72

122. 买卖股票的最佳时机 II

• 题目

  给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

  在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售。

  返回 你能获得的 最大 利润 。

  示例 1：

  1 2 3 4 5

  输入：prices = [7,1,5,3,6,4] 输出：7 解释：在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。 随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。 总利润为 4 + 3 = 7 。

  示例 2：

  1 2 3 4

  输入：prices = [1,2,3,4,5] 输出：4 解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。 总利润为 4 。

  示例 3：

  1 2 3

  输入：prices = [7,6,4,3,1] 输出：0 解释：在这种情况下, 交易无法获得正利润，所以不参与交易可以获得最大利润，最大利润为 0 。

• 题解

  贪心\动态规划

  官方题解

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

  // dp class Solution { public int maxProfit(int[] prices) { // dp[i][0]表示第i天不持有股票的最大利润，dp[i][1]表示第i天持有股票的最大利润 int[][] dp = new int[prices.length][2]; // 初始化 dp[0][0] = 0; dp[0][1] = -prices[0]; // 状态转移 for(int i=1;i<prices.length;i++){ // 不持有股票的利润，应该是前一天不持有股票和持有股票但是今天要卖出的最大利润 dp[i][0] = Math.max(dp[i-1][0],dp[i-1][1]+prices[i]); // 持有股票的利润，应该是前一天不持有股票，今天买入的和前一天持有股票的最大利润 dp[i][1] = Math.max(dp[i-1][0]-prices[i],dp[i-1][1]); } return dp[prices.length-1][0]; } } // dp 优化 class Solution { public int maxProfit(int[] prices) { // 初始化 int dp0 = 0; int dp1 = -prices[0]; // 状态转移 for(int i=1;i<prices.length;i++){ // 不持有股票的利润，应该是前一天不持有股票和持有股票但是今天要卖出的最大利润 dp0 = Math.max(dp0,dp1+prices[i]); // 持有股票的利润，应该是前一天不持有股票，今天买入的和前一天持有股票的最大利润 dp1 = Math.max(dp0-prices[i],dp1); } return dp0; } }

  例如：7,1,2,5,4,6,4 找局部递增序列，局部递增序列最小值买入，最大值卖出 先找最小值，再找较大值，遇到小的值就结束，找下一个最小值 由于递增序列内的数字序列：5-2+2-1 = 5-1 所以，我们可以再遇到一个正的利润就可以直接把这个利润加上即可，当然，也可以找出递增区间的最值的差值就是利润

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  class Solution { public int maxProfit(int[] prices) { int min = Integer.MAX_VALUE;// 最小值 int w = 0;// 利润 for(int i=0;i<prices.length;i++){ if(prices[i]-min>0){ w += prices[i]-min; min = Integer.MAX_VALUE; // 重置 } if(min>prices[i]){ min = prices[i]; } } return w; } }

day73

134. 加油站

• 题目

  在一条环路上有 n 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

  你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

  给定两个整数数组 gas 和 cost ，如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1 。如果存在解，则 保证 它是 唯一 的。

  示例 1:

  1 2 3 4 5 6 7 8 9 10

  输入: gas = [1,2,3,4,5], cost = [3,4,5,1,2] 输出: 3 解释: 从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油 开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油 开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油 开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油 开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油 开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。 因此，3 可为起始索引。

  示例 2:

  1 2 3 4 5 6 7 8 9

  输入: gas = [2,3,4], cost = [3,4,3] 输出: -1 解释: 你不能从 0 号或 1 号加油站出发，因为没有足够的汽油可以让你行驶到下一个加油站。 我们从 2 号加油站出发，可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油 开往 0 号加油站，此时油箱有 4 - 3 + 2 = 3 升汽油 开往 1 号加油站，此时油箱有 3 - 3 + 3 = 3 升汽油 你无法返回 2 号加油站，因为返程需要消耗 4 升汽油，但是你的油箱只有 3 升汽油。 因此，无论怎样，你都不可能绕环路行驶一周。

  提示:

  • gas.length == n
  • cost.length == n
  • 1 <= n <= 105
  • 0 <= gas[i], cost[i] <= 104

• 解法

  数学证明，降低时间复杂度

day74

135. 分发糖果

• 题目

  n 个孩子站成一排。给你一个整数数组 ratings 表示每个孩子的评分。

  你需要按照以下要求，给这些孩子分发糖果：

  • 每个孩子至少分配到 1 个糖果。
  • 相邻两个孩子评分更高的孩子会获得更多的糖果。

  请你给每个孩子分发糖果，计算并返回需要准备的 最少糖果数目 。

  示例 1：

  1 2 3

  输入：ratings = [1,0,2] 输出：5 解释：你可以分别给第一个、第二个、第三个孩子分发 2、1、2 颗糖果。

  示例 2：

  1 2 3 4

  输入：ratings = [1,2,2] 输出：4 解释：你可以分别给第一个、第二个、第三个孩子分发 1、2、1 颗糖果。 第三个孩子只得到 1 颗糖果，这满足题面中的两个条件。

  提示：

  • n == ratings.length
  • 1 <= n <= 2 * 104
  • 0 <= ratings[i] <= 2 * 104

• 解法

  方法一：两次遍历

  我们可以将「相邻的孩子中，评分高的孩子必须获得更多的糖果」这句话拆分为两个规则，分别处理。

  • 左规则：当 $\textit{ratings}[i - 1] < \textit{ratings}[i]$ 时，i 号学生的糖果数量将比 i - 1 号孩子的糖果数量多。
  • 右规则：当 $\textit{ratings}[i] > \textit{ratings}[i + 1]$ 时，i 号学生的糖果数量将比 i + 1 号孩子的糖果数量多。

  我们遍历该数组两次，处理出每一个学生分别满足左规则或右规则时，最少需要被分得的糖果数量。每个人最终分得的糖果数量即为这两个数量的最大值。

  具体地，以左规则为例：我们从左到右遍历该数组，假设当前遍历到位置 i，如果有 $\textit{ratings}[i - 1] < \textit{ratings}[i]$ 那么 i 号学生的糖果数量将比 i - 1 号孩子的糖果数量多，我们令 $\textit{left}[i] = \textit{left}[i - 1] + 1$ 即可，否则我们令 $\textit{left}[i] = 1$。

  在实际代码中，我们先计算出左规则 $\textit{left}$ 数组，在计算右规则的时候只需要用单个变量记录当前位置的右规则，同时计算答案即可。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

  // 形式一 class Solution { public int candy(int[] ratings) { // 每人先发一个糖果 int sum = ratings.length; // 挨个比较相邻评分的大小，分高者糖果数+1 int[] matrix = new int[ratings.length]; for(int i=1;i<ratings.length;i++){ if(ratings[i]>ratings[i-1]&&matrix[i]<=matrix[i-1]){ matrix[i]=matrix[i-1]+1; } } // System.out.println(Arrays.toString(matrix)); for(int i=ratings.length-2;i>=0;i--){ if(ratings[i]>ratings[i+1]&&matrix[i]<=matrix[i+1]){ matrix[i]=matrix[i+1]+1; } } // System.out.println(Arrays.toString(matrix)); for(int i=0;i<matrix.length;i++){sum+=matrix[i];} return sum; } } // 形式二 class Solution { public int candy(int[] ratings) { int n = ratings.length; int[] left = new int[n]; for (int i = 0; i < n; i++) { if (i > 0 && ratings[i] > ratings[i - 1]) { left[i] = left[i - 1] + 1; } else { left[i] = 1; } } int right = 0, ret = 0; for (int i = n - 1; i >= 0; i--) { if (i < n - 1 && ratings[i] > ratings[i + 1]) { right++; } else { right = 1; } ret += Math.max(left[i], right); } return ret; } }

  方法二：常数空间遍历

  https://leetcode.cn/problems/candy/solution/fen-fa-tang-guo-by-leetcode-solution-f01p/

day75

376. 摆动序列

• 题目

  如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为 **摆动序列 。**第一个差（如果存在的话）可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。

  • 例如， [1, 7, 4, 9, 2, 5] 是一个 摆动序列 ，因为差值 (6, -3, 5, -7, 3) 是正负交替出现的。
  • 相反，[1, 4, 7, 2, 5] 和 [1, 7, 4, 5, 5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

  子序列 可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。

  给你一个整数数组 nums ，返回 nums 中作为 摆动序列 的 最长子序列的长度 。

  示例 1：

  1 2 3

  输入：nums = [1,7,4,9,2,5] 输出：6 解释：整个序列均为摆动序列，各元素之间的差值为 (6, -3, 5, -7, 3) 。

  示例 2：

  1 2 3 4

  输入：nums = [1,17,5,10,13,15,10,5,16,8] 输出：7 解释：这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ，各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。

  示例 3：

  1 2	输入：nums = [1,2,3,4,5,6,7,8,9] 输出：2

  提示：

  • 1 <= nums.length <= 1000
  • 0 <= nums[i] <= 1000

  **进阶：**你能否用 O(n) 时间复杂度完成此题?

• 解法

  动态规划\贪心算法

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  class Solution { public int wiggleMaxLength(int[] nums) { // 顺序遍历，“峰”才算上：一旦遇到非递增数据或者非递减数据，就算做最长子序列的一个元素 if(nums.length==1){ return 1; }else if(nums.length==2&&nums[0]!=nums[1]){ return 2; } int ans = 1; int state = 0; //表示先前的状态：0表示前面的两个数差为0，1表示差为正，-1表示差为负 // 只需计数“峰”的数量即可 for(int i=1;i<nums.length;i++){ if(nums[i]<nums[i-1]&&state==1){ ans++; state = -1; }else if(nums[i]>nums[i-1]&&state==-1){ ans++; state = 1; }else if(nums[i]>nums[i-1]&&state==0){ ans++; state = 1; }else if(nums[i]<nums[i-1]&&state==0){ ans++; state = -1; } } return ans; } }

day76

409. 最长回文串

• 题目

  给定一个包含大写字母和小写字母的字符串 s ，返回 通过这些字母构造成的 最长的回文串 。

  在构造过程中，请注意 区分大小写 。比如 "Aa" 不能当做一个回文字符串。

  示例 1:

  1 2 3 4

  输入:s = "abccccdd" 输出:7 解释: 我们可以构造的最长的回文串是"dccaccd", 它的长度是 7。

  示例 2:

  1 2	输入:s = "a" 输入:1

  示例 3：

  1 2	输入:s = "aaaaaccc" 输入:7

  提示:

  • 1 <= s.length <= 2000
  • s 只由小写 和/或 大写英文字母组成

• 解法

  解法一：数学规律

  题目要求仅仅只是需要根据给出的字符序列构造出最长回文串序列，回文串的长度如果是偶数那么前一半字符序列是后一半字符序列的“镜像”；如果是奇数，那么中间会有一个字符作为分隔，左右两边是“镜像”关系。针对“镜像”字符序列，也就是说，一个字符重复n次，如果n是偶数，那么可以将这些字符一半放在左边，一半放在右边；如果是奇数，那么可以去掉一个字符，然后将一半放左边，一半放右边。如果给的字符序列里存在奇数个重复字符，都可以作为“镜像”序列的地中情况；如果都是偶数，那么只能构造第一个“镜像”字符序列。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

  class Solution { public int longestPalindrome(String s) { if(s.length()==1) return 1; // 先字典排序 char[] chs = s.toCharArray(); Arrays.sort(chs); // System.out.println(Arrays.toString(chs)); char pre = chs[0]; int count = 1; int[] counts = new int[chs.length]; int countIdx = 0; for(int i=1;i<chs.length;i++){ if(chs[i]==pre){ count++; }else{ // 暂存 counts[countIdx] = count; countIdx++; count=1; pre = chs[i]; } } counts[countIdx]=count; // System.out.println(Arrays.toString(counts)); int Len = 1; boolean flag = false; for(int i=0;i<counts.length&&counts[i]!=0;i++){ if(counts[i]%2==0){ Len+=counts[i]; }else{ if(counts[i]>1){ Len+=counts[i]-1; } flag=true; } } return flag?Len:Len-1; } }

  解法二：官方解法

  https://leetcode.cn/problems/longest-palindrome/solution/zui-chang-hui-wen-chuan-by-leetcode-solution/

day77

435. 无重叠区间

• 题目

  给定一个区间的集合 intervals ，其中 intervals[i] = [starti, endi] 。返回 需要移除区间的最小数量，使剩余区间互不重叠 。

  示例 1:

  1 2 3

  输入: intervals = [[1,2],[2,3],[3,4],[1,3]] 输出: 1 解释: 移除 [1,3] 后，剩下的区间没有重叠。

  示例 2:

  1 2 3

  输入: intervals = [ [1,2], [1,2], [1,2] ] 输出: 2 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

  示例 3:

  1 2 3

  输入: intervals = [ [1,2], [2,3] ] 输出: 0 解释: 你不需要移除任何区间，因为它们已经是无重叠的了。

  提示:

  • 1 <= intervals.length <= 105
  • intervals[i].length == 2
  • -5 * 104 <= starti < endi <= 5 * 104

• 解法

  动态规划\贪心

day78

452. 用最少数量的箭引爆气球

• 题目

  有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

  一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 x``start，x``end， 且满足 xstart ≤ x ≤ x``end，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

  给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

  示例 1：

  1 2 3 4 5

  输入：points = [[10,16],[2,8],[1,6],[7,12]] 输出：2 解释：气球可以用2支箭来爆破: -在x = 6处射出箭，击破气球[2,8]和[1,6]。 -在x = 11处发射箭，击破气球[10,16]和[7,12]。

  示例 2：

  1 2 3

  输入：points = [[1,2],[3,4],[5,6],[7,8]] 输出：4 解释：每个气球需要射出一支箭，总共需要4支箭。

  示例 3：

  1 2 3 4 5

  输入：points = [[1,2],[2,3],[3,4],[4,5]] 输出：2 解释：气球可以用2支箭来爆破: - 在x = 2处发射箭，击破气球[1,2]和[2,3]。 - 在x = 4处射出箭，击破气球[3,4]和[4,5]。

  提示:

  • 1 <= points.length <= 105
  • points[i].length == 2
  • -231 <= xstart < xend <= 231 - 1

• 解法

  注意给出的数据有大数，所以涉及到运算，不能直接向加减乘除等。

  解法一：暴力

  问题可以看成是：我们删除一些重叠的区间，之后再统计这些没有删除的区间

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

  class Solution { public int findMinArrowShots(int[][] points) { if(points.length==1) return 1; // 按照右端点排序 Arrays.sort(points, new Comparator<int[]>() { public int compare(int[] point1, int[] point2) { if (point1[1] > point2[1]) { return 1; } else if (point1[1] < point2[1]) { return -1; } else { return 0; } } }); // 记录是否删除区间 boolean[] isDel = new boolean[points.length]; int ans = 0; // 基准区间的左右值 for(int i=0;i<points.length;i++){ if(!isDel[i]){ int pivotLeft = points[i][0]; int pivotRight = points[i][1]; for(int j=i+1;j<points.length;j++){ // 当前区间还在 if(!isDel[j]){ if(points[j][0]>pivotRight){} else{ isDel[j] = true; } } } } } for(int i=0;i<isDel.length;i++){ if(!isDel[i]){ ans++; } } return ans; } }

解法二：排序+贪心

day79

455. 分发饼干

• 题目

  假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

  对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

  示例 1:

  1 2 3 4 5 6

  输入: g = [1,2,3], s = [1,1] 输出: 1 解释: 你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。 虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。 所以你应该输出1。

  示例 2:

  1 2 3 4 5 6

  输入: g = [1,2], s = [1,2,3] 输出: 2 解释: 你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。 你拥有的饼干数量和尺寸都足以让所有孩子满足。 所以你应该输出2.

  提示：

  • 1 <= g.length <= 3 * 104
  • 0 <= s.length <= 3 * 104
  • 1 <= g[i], s[j] <= 231 - 1

• 解法

  排序+双指针+贪心

day80

605. 种花问题

• 题目

  假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

  给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。

  示例 1：

  1 2	输入：flowerbed = [1,0,0,0,1], n = 1 输出：true

  示例 2：

  1 2	输入：flowerbed = [1,0,0,0,1], n = 2 输出：false

  提示：

  • 1 <= flowerbed.length <= 2 * 104
  • flowerbed[i] 为 0 或 1
  • flowerbed 中不存在相邻的两朵花
  • 0 <= n <= flowerbed.length

• 解法

  解法一：模拟

  触雷首尾位置需要特殊处理，其余位置就是比较前一个和后一个是否都没种花，如果都没种花，再看当前位置是否种花，如果没，就种花，否则就需要迭代下一个花坛位置

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { public boolean canPlaceFlowers(int[] flowerbed, int n) { if(flowerbed.length==1){ if(flowerbed[0]==1) return n==0; else return n<=1; } for(int i=0;i<flowerbed.length;i++){ // 当碰到收尾时，需要收敛比较 if(i==0){ if(flowerbed[i]!=flowerbed[i+1]){}else { if(n==0) break; flowerbed[i]=1; n--; } }else if(i==flowerbed.length-1){ if(flowerbed[i]!=flowerbed[i-1]){}else { if(n==0) break; flowerbed[i]=1; n--; } }else{ if(flowerbed[i]!=flowerbed[i-1]||flowerbed[i]!=flowerbed[i+1]){} else { if(n==0) break; flowerbed[i]=1; n--; } } } // System.out.println(Arrays.toString(flowerbed)); return n==0; } }

  解法二：贪心

  https://leetcode.cn/problems/can-place-flowers/solution/chong-hua-wen-ti-by-leetcode-solution-sojr/

day81

738. 单调递增的数字

• 题目

  当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。

  给定一个整数 n ，返回 小于或等于 n 的最大数字，且数字呈 单调递增 。

  示例 1:

  1 2	输入: n = 10 输出: 9

  示例 2:

  1 2	输入: n = 1234 输出: 1234

  示例 3:

  1 2	输入: n = 332 输出: 299

  提示:

  • 0 <= n <= 109

• 解法

  解法一：数学规律

  我们只需要找到单调递增的最后一个数位上的数字，如果该数字是最后一个，那么整体都满足单调递增特性直接返回；如果不是，那么当前数位和前面的数位组成的数字减去1，再把后面的数位全部变成数字9，之后前面和后面凭借在一起返回即可

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56

  class Solution { public int monotoneIncreasingDigits(int n) { // 取位数 int Len = 0; int tmp = n; while(tmp!=0){ tmp=tmp/10; Len++; } // System.out.println("位数"+Len); // 如果是一位直接返回结果 if(Len==1) return n; // 其他位数，循环处理 tmp = n; // 保证单调递增 int preMax = 0; int curMax = 0; int index = 0; while(index<Len){ // 取出当前位 curMax = tmp/(int)Math.pow(10,Len-index-1)%10; // System.out.println("preMax="+preMax+"curMax="+curMax); if(curMax<preMax){ // 往前回溯分割点 int i = index-1; while(i>=0){ if(tmp/(int)Math.pow(10,Len-i-1)%10!=preMax){ break; } i--; } i++; // System.out.println("回溯次数="+i); // 将该位及以前的数据减去（该位数字+1），再和后面等位数的数字9拼接 // int lastCast = tmp/(int)Math.pow(10,Len-i-1); // System.out.println("lastCast="+lastCast); int front = tmp/(int)Math.pow(10,Len-i-1)-1; int back = 0; int j=Len-i-1; while(j>0){ back=back*10+9; j--; } // System.out.println("front="+front+"back="+back); return front*((int)Math.pow(10,Len-i-1))+back; } preMax = curMax; index++; } return n; } }

解法二：贪心

https://leetcode.cn/problems/monotone-increasing-digits/solution/dan-diao-di-zeng-de-shu-zi-by-leetcode-s-5908/

day82

1005. K 次取反后最大化的数组和

• 题目

  给你一个整数数组 nums 和一个整数 k ，按以下方法修改该数组：

  • 选择某个下标 i 并将 nums[i] 替换为 -nums[i] 。

  重复这个过程恰好 k 次。可以多次选择同一个下标 i 。

  以这种方式修改数组后，返回数组 可能的最大和 。

  示例 1：

  1 2 3

  输入：nums = [4,2,3], k = 1 输出：5 解释：选择下标 1 ，nums 变为 [4,-2,3] 。

  示例 2：

  1 2 3

  输入：nums = [3,-1,0,2], k = 3 输出：6 解释：选择下标 (1, 2, 2) ，nums 变为 [3,1,0,2] 。

  示例 3：

  1 2 3

  输入：nums = [2,-3,-1,5,-4], k = 2 输出：13 解释：选择下标 (1, 4) ，nums 变为 [2,3,-1,5,4] 。

  提示：

  • 1 <= nums.length <= 104
  • -100 <= nums[i] <= 100
  • 1 <= k <= 104

• 解法

  解法一：寻找数学规律

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57

  // 代码一 class Solution { public int largestSumAfterKNegations(int[] nums, int k) { Arrays.sort(nums); for(int i=0;i<nums.length;i++){ if(k<=0) break; if(nums[i]<0) { nums[i]*=-1; k--; } } // 可以通过找最值，省去第二次排序懒得写了 Arrays.sort(nums); int sum = 0; // System.out.println(Arrays.toString(nums)); // 找和 for(int i=0;i<nums.length;i++){ sum+=nums[i]; } return k%2==1?sum-2*nums[0]:sum; } } // 官方解法 class Solution { public int largestSumAfterKNegations(int[] nums, int k) { Map<Integer, Integer> freq = new HashMap<Integer, Integer>(); for (int num : nums) { freq.put(num, freq.getOrDefault(num, 0) + 1); } int ans = Arrays.stream(nums).sum(); for (int i = -100; i < 0; ++i) { if (freq.containsKey(i)) { int ops = Math.min(k, freq.get(i)); ans += (-i) * ops * 2; freq.put(i, freq.get(i) - ops); freq.put(-i, freq.getOrDefault(-i, 0) + ops); k -= ops; if (k == 0) { break; } } } if (k > 0 && k % 2 == 1 && !freq.containsKey(0)) { for (int i = 1; i <= 100; ++i) { if (freq.containsKey(i)) { ans -= i * 2; break; } } } return ans; } }

day83

1013. 将数组分成和相等的三个部分

• 题目

  给你一个整数数组 arr，只有可以将其划分为三个和相等的 非空 部分时才返回 true，否则返回 false。

  形式上，如果可以找出索引 i + 1 < j 且满足 (arr[0] + arr[1] + ... + arr[i] == arr[i + 1] + arr[i + 2] + ... + arr[j - 1] == arr[j] + arr[j + 1] + ... + arr[arr.length - 1]) 就可以将数组三等分。

  示例 1：

  1 2 3

  输入：arr = [0,2,1,-6,6,-7,9,1,2,0,1] 输出：true 解释：0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1

  示例 2：

  1 2	输入：arr = [0,2,1,-6,6,7,9,-1,2,0,1] 输出：false

  示例 3：

  1 2 3

  输入：arr = [3,3,6,5,-2,2,5,1,-9,4] 输出：true 解释：3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4

  提示：

  • 3 <= arr.length <= 5 * 104
  • -104 <= arr[i] <= 104

• 解法

  解法一：暴力法

  题目要求求出是否存在三个相等的划分。显而易见，我们可以暴力。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  class Solution { public boolean canThreePartsEqualSum(int[] arr) { // 先放第一个挡板 for(int i=0;i<arr.length-2;i++){ // 继续放第二个挡板 for(int j=i+1;j<arr.length-1;j++){ int firstPart = sum(0,i,arr); // System.out.println(firstPart+"-"+sum(i+1,j,arr)+"-"+sum(j+1,arr.length-1,arr)); if(firstPart==sum(i+1,j,arr)){ if(firstPart==sum(j+1,arr.length-1,arr)){ return true; } } } } return false; } public int sum(int l,int r,int[] arr){ int sum=0; for(;l<=r;l++){ sum+=arr[l]; } return sum; } }

  遗憾的是，暴力算法的时间复杂度为O(n^3^)。问题出现在，每次求和都需要重新计算和。可以使用前缀和的方式优化一下算法

  解法二：前缀和优化

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public boolean canThreePartsEqualSum(int[] arr) { int sum = 0; for(int i=0;i<arr.length;i++){ sum+=arr[i]; } int firstSum = 0; int secondSum = 0; // 先放第一个挡板 for(int i=0;i<arr.length-2;i++){ firstSum +=arr[i]; // 继续放第二个挡板 for(int j=i+1;j<arr.length-1;j++){ secondSum += arr[j]; // System.out.println(firstSum+"-"+secondSum+"-"+(sum-firstSum-secondSum)); if(firstSum==secondSum){ if(firstSum==sum-firstSum-secondSum){ return true; } } } secondSum=0; } return false; } }

  解法三：贪心

  发现数学规律，寻找切分点

day84

392. 判断子序列

• 题目

  给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

  字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

  进阶：

  如果有大量输入的 S，称作 S1, S2, … , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

  致谢：

  特别感谢 @pbrother 添加此问题并且创建所有测试用例。

  示例 1：

  1 2	输入：s = "abc", t = "ahbgdc" 输出：true

  示例 2：

  1 2	输入：s = "axc", t = "ahbgdc" 输出：false

  提示：

  • 0 <= s.length <= 100
  • 0 <= t.length <= 10^4
  • 两个字符串都只由小写字符组成。

• 解法

  解法一：双指针

  https://leetcode.cn/problems/is-subsequence/solution/pan-duan-zi-xu-lie-by-leetcode-solution/

  解法二：动态规划

  https://leetcode.cn/problems/is-subsequence/solution/shi-pin-jiang-jie-dong-tai-gui-hua-qiu-jie-is-subs/

  比官方题解稍微好理解一点

day85

62. 不同路径

• 题目

  一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

  机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

  问总共有多少条不同的路径？

  示例 1：

  

  1 2	输入：m = 3, n = 7 输出：28

  示例 2：

  1 2 3 4 5 6 7

  输入：m = 3, n = 2 输出：3 解释： 从左上角开始，总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下

  示例 3：

  1 2	输入：m = 7, n = 3 输出：28

  示例 4：

  1 2	输入：m = 3, n = 3 输出：6

  提示：

  • 1 <= m, n <= 100
  • 题目数据保证答案小于等于 2 * 109

• 解法

  动态规划/组合数学

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public int uniquePaths(int m, int n) { // 定义状态：dp[i][j]表示移动到i行j列位置有多少条路径 long[][] dp = new long[m][n]; // 初始状态：第一行和第一列都只有一条路径 for(int i=0;i<m;i++){ dp[i][0] = 1; } for(int i=0;i<n;i++){ dp[0][i] = 1; } // 状态转移方程：dp[i][j]显然是由dp[i-1][j]或dp[i][j-1]转移而来，那么结果应该取二者之和 for(int i=1;i<m;i++){ for(int j=1;j<n;j++){ dp[i][j] = dp[i-1][j]+dp[i][j-1]; } } return (int)dp[m-1][n-1]; } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  func uniquePaths(m int, n int) int { dp := make([][]int,m) for i:=0;i<m;i++{ dp[i] = make([]int,n) dp[i][0] = 1 } for j:=0;j<n;j++{ dp[0][j] = 1 } // 状态转移 for i:=1;i<m;i++{ for j:=1;j<n;j++{ dp[i][j] = dp[i-1][j]+dp[i][j-1] } } return dp[m-1][n-1] }

day86

63. 不同路径 II

• 题目

  一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

  机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

  现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

  网格中的障碍物和空位置分别用 1 和 0 来表示。

  示例 1：

  

  1 2 3 4 5 6

  输入：obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]] 输出：2 解释：3x3 网格的正中间有一个障碍物。 从左上角到右下角一共有 2 条不同的路径： 1. 向右 -> 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 -> 向右

  示例 2：

  

  1 2	输入：obstacleGrid = [[0,1],[0,0]] 输出：1

  提示：

  • m == obstacleGrid.length
  • n == obstacleGrid[i].length
  • 1 <= m, n <= 100
  • obstacleGrid[i][j] 为 0 或 1

• 解法

  解法一：动态规划

  思路和上一道题一样，都满足动态规划的几个条件

  官方动态规划题解

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36

  class Solution { public int uniquePathsWithObstacles(int[][] obstacleGrid) { int rowNum = obstacleGrid.length; int spanNum = obstacleGrid[0].length; int[][] dp = new int[rowNum][spanNum]; // 初始化dp for(int i=0;i<rowNum;i++){ if(obstacleGrid[i][0]==1){ break; } dp[i][0] = 1; } for(int i=0;i<spanNum;i++){ if(obstacleGrid[0][i]==1){ break; } dp[0][i] = 1; } // System.out.println(rowNum+"-"+spanNum); // 状态转移 for(int i=1;i<rowNum;i++){ for(int j=1;j<spanNum;j++){ if(obstacleGrid[i][j]==0){ dp[i][j]=dp[i-1][j]+dp[i][j-1]; // System.out.println(dp[i][j]+"="+dp[i-1][j]+"+"+dp[i][j-1]); } } } //最后结果 return dp[rowNum-1][spanNum-1]; } }

day87

64. 最小路径和

• 题目

  给定一个包含非负整数的 *m* x *n* 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

  **说明：**每次只能向下或者向右移动一步。

  示例 1：

  

  1 2 3

  输入：grid = [[1,3,1],[1,5,1],[4,2,1]] 输出：7 解释：因为路径 1→3→1→1→1 的总和最小。

  示例 2：

  1 2	输入：grid = [[1,2,3],[4,5,6]] 输出：12

  提示：

  • m == grid.length
  • n == grid[i].length
  • 1 <= m, n <= 200
  • 0 <= grid[i][j] <= 100

• 解法

  解法一：动态规划

  https://leetcode.cn/problems/minimum-path-sum/solution/zui-xiao-lu-jing-he-by-leetcode-solution/

  这题和不同的路径的状态转移方程有点类似

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  func minPathSum(grid [][]int) int { m:=len(grid) n:=len(grid[0]) dp := make([][]int,m) s:=0 for i:=0;i<m;i++{ dp[i] = make([]int,n) dp[i][0] = s + grid[i][0] s = dp[i][0] } s=0 for j:=0;j<n;j++{ dp[0][j] =s + grid[0][j] s = dp[0][j] } for i:=1;i<m;i++{ for j:=1;j<n;j++{ if dp[i-1][j]>dp[i][j-1]{ dp[i][j] = dp[i][j-1]+grid[i][j] }else{ dp[i][j] = dp[i-1][j]+grid[i][j] } } } // fmt.Println(dp) return dp[m-1][n-1] }

day88

70. 爬楼梯

• 题目

  假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

  每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

  示例 1：

  1 2 3 4 5

  输入：n = 2 输出：2 解释：有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶

  示例 2：

  1 2 3 4 5 6

  输入：n = 3 输出：3 解释：有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶

  提示：

  • 1 <= n <= 45

• 解法

  官方题解：动态规划/矩阵快速幂/通项公式/

  dp应该是最简单的

  https://leetcode.cn/problems/climbing-stairs/solution/pa-lou-ti-by-leetcode-solution/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public int climbStairs(int n) { if(n<=2) return n; // 状态表示：dp[i]表示爬第i层楼梯的方法总数 int[] dp = new int[n+1]; // 状态初始化 //dp[0] = 1;// 没有意义，为了凑数,也可以置为1；也可以当作非法状态看待 dp[1] = 1;// 当爬第一层时，只有一种方法：爬一个台阶 // 状态转移方程：dp[i]是由dp[i-1]或dp[i-2]转移过来，那么显然方法总数就是前两者之和; dp[2] = 2; for(int i=3;i<=n;i++){ dp[i] = dp[i-1] + dp[i-2]; } return dp[n]; } }

  还可以将这个问题看成是“物品的重量分别是1和2，背包的容量是n”的完全背包问题。

  二维DP解法：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  class Solution { public int climbStairs(int n) { if(n<=2) return n; // 状态表示：dp[i][j]表示取前i物品，装下容量j的方法数，注意此处要排列数 int[][] dp = new int[3][n+1]; int[] w = new int[]{1,2}; // 状态初始化：取前i个物品装容量为0，只有一种方法，那就是什么都不取 dp[0][0]=1; // 状态转移 // 二维dp的顺序无所谓 for(int i=1;i<=2;i++){ for(int j=0;j<=n;j++){ if(j>=w[i-1]) { // 每次可以放的时候，都是取前0-i个数的和，这样才是排列数。 // 可以画出dp转移表验证一下。 //（其实这是画表时候找到的规律。感觉是一种数学定律） for(int k=0;k<i;k++){ dp[i][j] += dp[i][j-w[k]]; } } else dp[i][j] = dp[i-1][j]; } } // System.out.println(Arrays.deepToString(dp)); return dp[2][n]; } }

  一维dp解法，这里的一维dp不再是优化二维得来的了。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public int climbStairs(int n) { if(n<=2) return n; // 状态表示：dp[j]表示装下容量j的方法数，注意此处要排列数 int[] dp = new int[n+1]; int[] w = new int[]{1,2}; // 状态初始化：装容量为0，只有一种方法，那就是什么都不取 dp[0]=1; // 状态转移 for(int j=0;j<=n;j++){ for(int i=1;i<=2;i++){ if(j>=w[i-1]) { dp[j] += dp[j-w[i-1]]; } } } // System.out.println(Arrays.toString(dp)); return dp[n]; } }

day89

72. 编辑距离

• 题目

  给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

  你可以对一个单词进行如下三种操作：

  • 插入一个字符
  • 删除一个字符
  • 替换一个字符

  示例 1：

  1 2 3 4 5 6

  输入：word1 = "horse", word2 = "ros" 输出：3 解释： horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')

  示例 2：

  1 2 3 4 5 6 7 8

  输入：word1 = "intention", word2 = "execution" 输出：5 解释： intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')

  提示：

  • 0 <= word1.length, word2.length <= 500
  • word1 和 word2 由小写英文字母组成

• 解法

  方法一：动态规划找编辑距离

  好理解的图表解法

  官方题解

day90

分解质因数

• 题目

  问题描述

  　　求出区间[a,b]中所有整数的质因数分解。

  输入格式

  　　输入两个整数a，b。

  输出格式

  　　每行输出一个数的分解，形如k=a1a2a3…(a1<=a2<=a3…，k也是从小到大的)(具体可看样例)

  样例输入

  1

  3 10

  样例输出

  1 2 3 4 5 6 7 8

  3=3 4=2*2 5=5 6=2*3 7=7 8=2*2*2 9=3*3 10=2*5

  提示

  　　先筛出所有素数，然后再分解。

  数据规模和约定

  　　2<=a<=b<=10000

• 解法

  思路：这道题的暴力解法思路显而易见：对区间内的每一个数都进行质因数分解。但是这样做显然做了很多的重复计算，我们可以利用空间换时间的原理，将第一次计算出来的结果保存好，这样第二次再计算时，直接拿出来用即可，这样就避免了大量的重复计算

  代码演示

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  import java.util.*; public class Main{ public static void main(String args[]){ Scanner sc = new Scanner(System.in); int a = sc.nextInt(); int b = sc.nextInt(); String[] dict = new String[b+1]; dict[2] = "2*"; dict[3] = "3*"; // System.out.println("2=2"); for(int i=2;i<=b;i++) { int tmp = i; boolean flag = true; // 算质因数 for(int n=2;n<i&&tmp>=1;n++) { // 找到的第一个最小因子n，就是质因数。再拆分剩余因子 if(tmp%n==0) { flag = false; // 将第一个因子拼凑在tmp位置上 if(dict[n]!=null) { dict[tmp]=dict[n]; }else { dict[tmp] = n+"*"; } // 剩余因子的记忆化搜索，降低时间复杂度 if(dict[tmp/n]!=null) { dict[tmp]=dict[tmp]+dict[tmp/n]; break; } // 迭代剩余因子的分解，需要重新开始 tmp = tmp/n; n=2; } } // 如果i为素数，那么i就没有因子，所以需要直接初始化dict if(flag) { dict[i] = i+"*"; } if(i>=a) { if(dict[i].length()>1&&dict[i].charAt(dict[i].length()-1)=='*') { System.out.println(i+"="+dict[i].substring(0, dict[i].length()-1)); }else System.out.println(i+"="+dict[i]); } } //System.out.print(Arrays.toString(dict)); sc.close(); }

day91

最大分解

• 题目

  问题描述

  　　给出一个正整数n，求一个和最大的序列a0，a1，a2，……，ap，满足n=a0>a1>a2>……>ap且ai+1是ai的约数，输出a1+a2+……+ap的最大值

  输入格式

  　　输入仅一行，包含一个正整数n

  输出格式

  　　一个正整数，表示最大的序列和，即a1+a2+……+ap的最大值

  样例输入

  10

  样例输出

  6

  数据规模和约定

  　　1<n<=10^6

  样例说明

  　　p=2 　　a0=10，a1=5，a2=1，6=5+1

• 解法

  主要采用dfs+贪心优化

  思路：这个题目本身就是不断得分解得到约数，显而易见应该使用递归编程求解；我们再思考题目：题目的意思是让我们找出约数序列和得最大值，可以验证这种贪心策略：每次都取最大约数，这样得到的结果总是当前最优，这样每一步的最优解的和自然是最终的最大值。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

  import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc =new Scanner(System.in); System.out.print(dfs(sc.nextInt())); sc.close(); } // dfs+贪心优化 public static int dfs(int num) { // 判断当前数是否是素数，是的话就停止当前分支递归 if(num<=3) return 1; boolean flag = false; for(int i=2;i<num;i++) { if(num%i==0) { flag =true; // 找到第一个约数i，也就是最小得那个约数i;就去递归最大得那个约数 // System.out.println(num+"|"+num/i+"|"+i); return dfs(num/i)+num/i; } } // 素数 if(!flag) { return 1; } return 1; } }

day92

46. 全排列

• 题目

  给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

  示例 1：

  1 2	输入：nums = [1,2,3] 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

  示例 2：

  1 2	输入：nums = [0,1] 输出：[[0,1],[1,0]]

  示例 3：

  1 2	输入：nums = [1] 输出：[[1]]

  提示：

  • 1 <= nums.length <= 6
  • -10 <= nums[i] <= 10
  • nums 中的所有整数 互不相同

• 解法

  解法一：dfs+回溯

  这个问题可以看作有 n 个排列成一行的空格，我们需要从左往右依此填入题目给定的 n 个数，每个数只能使用一次。那么很直接的可以想到一种穷举的算法，即从左往右每一个位置都依此尝试填入一个数，看能不能填完这 n 个空格，在程序中我们可以用「回溯法」来模拟这个过程。

  DFS+回溯

  解法二：dfs+回溯+哈希去重

  全排列可以从【组合数】里筛选出来，利用哈希表去重。同时，需要注意深度拷贝的问题

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { HashSet<Integer> hm; public Solution(){ hm = new HashSet<>(); } public List<List<Integer>> permute(int[] nums) { List<List<Integer>> lls = new ArrayList<>(); dfs(lls,new ArrayList<>(),nums,nums.length,0); return lls; } public void dfs(List<List<Integer>> lls,List<Integer> ls,int[] nums,int len,int step){ if(step==len){ // 核心关键: ls是引用类型,所以此处要深拷贝出来 lls.add(new ArrayList<>(ls)); return; } for(int i=0;i<len;i++){ if (hm.contains(nums[i])){ continue; } ls.add(nums[i]); hm.add(nums[i]); dfs(lls,ls,nums,len,step+1); hm.remove(nums[i]); ls.remove(ls.size()-1); } } } // 全排列不去重

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  func permute(nums []int) [][]int { ans := [][]int{} used := make([]bool,len(nums)) var dfs func(nums []int,item []int,step int) dfs = func(nums []int,item []int,step int){ if step==len(nums){ newItem:=make([]int,len(item)) copy(newItem,item) ans = append(ans,newItem) return } for i:=0;i<len(nums);i++{ if used[i] { continue } item = append(item,nums[i]) used[i] = true dfs(nums,item,step+1) used[i] = false item = item[:len(item)-1] } } dfs(nums,[]int{},0) return ans }

day93

马虎的算式

• 题目

  小明是个急性子，上小学的时候经常把老师写在黑板上的题目抄错了。有一次，老师出的题目是：36 x 495 = ? 他却给抄成了：396 x 45 = ?但结果却很戏剧性，他的答案竟然是对的！！因为 36 * 495 = 396 * 45 = 17820 类似这样的巧合情况可能还有很多，比如：27 * 594 = 297 * 54 假设 a b c d e 代表1~9不同的5个数字（注意是各不相同的数字，且不含0）能满足形如： ab * cde = adb * ce 这样的算式一共有多少种呢？请你利用计算机的优势寻找所有的可能，并回答不同算式的种类数。满足乘法交换律的算式计为不同的种类，所以答案肯定是个偶数。

• 解法

  解法一：暴力枚举

  题目的意思就是在1~9里找到五个不同的数字组合，满足题目的要求。直接五个for循环嵌套解决

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  public class Main { public static void main(String[] args){ int a,b,c,d,e; int count=0;//记录满足条件的个数 for(a=1;a<=9;a++) for(b=1;b<=9;b++) for(c=1;c<=9;c++) for(d=1;d<=9;d++) for(e=1;e<=9;e++){//abcde代表1-9各不同的5个数字 if(a!=b&&a!=c&&a!=d&&a!=e&&b!=c&&b!=d&&b!=e &&c!=d&&c!=e&&d!=e){ int sum1=(a*10+b)*(c*100+d*10+e); int sum2=(a*100+d*10+b)*(c*10+e); if(sum1==sum2) { count++; } } } System.out.println(count); } }

  解法二：优雅的DFS+回溯

  我们可以通过dfs搜索解决。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  import java.util.Arrays; public class Main { static int[] nums = {1,2,3,4,5,6,7,8,9}; static boolean[] vs = new boolean[9]; static int count = 0; public static void main(String[] args) { dfs(new int[5],0); System.out.print(count); } // DFS枚举: 找出五个数的所有组合 public static void dfs(int[] zuhe,int step) { if(step>4) { // 处理五个数 int a = zuhe[0]*10+zuhe[1]; int b = zuhe[2]*100+zuhe[3]*10+zuhe[4]; int c = zuhe[0]*100+zuhe[3]*10+zuhe[1]; int d = zuhe[2]*10+zuhe[4]; if(a*b==c*d) { // System.out.println(Arrays.toString(zuhe)); count++; } return; } for(int i=0;i<nums.length;i++) { // 取出没有被拿的数，保证每位数字都不一样 if(!vs[i]) { vs[i]=true; zuhe[step]=nums[i]; dfs(zuhe,step+1); vs[i]=false;// 回溯 zuhe[step]=0; // 回溯 } } } }

day94

振兴中华

• 题目

  小明参加了学校的趣味运动会，其中的一个项目是：跳格子。地上画着一些格子，每个格子里写一个字，如下所示：（也可参见p1.jpg）

  从我做起振 我做起振兴 做起振兴中 起振兴中华

  比赛时，先站在左上角的写着“从”字的格子里，可以横向或纵向跳到相邻的格子里，但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。 要求跳过的路线刚好构成“从我做起振兴中华”这句话。 请你帮助小明算一算他一共有多少种可能的跳跃路线呢？

• 解法

  解法一：DFS

  思路：只要每次都是往右或往左走，就一定满足题目要求。所以，就是求这样走的路径有多少。显然，可以通过DFS直接模拟这个过程。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  public class Main { static String[][] matrix = { {"从","我","做,","起","振"}, {"我","做,","起","振","兴"}, {"做,","起","振","兴","中"}, {"起","振","兴","中","华"} }; public static void main(String[] args) { System.out.print(dfs(0,0)); } public static int dfs(int i,int j) { if(i==3||j==4) { return 1; } // 下一步走,且回溯前面往下走的步数，换一种往右走 return dfs(i+1,j)+dfs(i,j+1); } }

day95

123. 买卖股票的最佳时机 III

• 题目

  给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

  设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

  **注意：**你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

  示例 1:

  1 2 3 4

  输入：prices = [3,3,5,0,0,3,1,4] 输出：6 解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。 随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天 （股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3 。

  示例 2：

  1 2 3 4 5

  输入：prices = [1,2,3,4,5] 输出：4 解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。 因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

  示例 3：

  1 2 3

  输入：prices = [7,6,4,3,1] 输出：0 解释：在这个情况下, 没有交易完成, 所以最大利润为 0。

  示例 4：

  1 2	输入：prices = [1] 输出：0

  提示：

  • 1 <= prices.length <= 105
  • 0 <= prices[i] <= 105

• 解法

  动态规划

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class Solution { public int maxProfit(int[] prices) { // 状态定义：dp[i][0]表示没有操作 // dp[i][1]表示前i天第一次持有股票的最大利润 // dp[i][2]表示前i天第一次卖出股票的最大利润 // dp[i][3]表示前i天第二次持有股票的最大利润 // dp[i][4]表示前i天第二次卖出股票的最大利润 int[][] dp = new int[prices.length+1][5]; // 初始化 dp[0][0] = 0; dp[0][2] =0; dp[0][1] = -prices[0]; dp[0][3] = -prices[0]; for(int i=1;i<=prices.length;i++){ dp[i][1] = Math.max(dp[i-1][0]-prices[i-1],dp[i-1][1]); dp[i][2] = Math.max(dp[i-1][1]+prices[i-1],dp[i-1][2]); dp[i][3] = Math.max(dp[i-1][2]-prices[i-1],dp[i-1][3]); dp[i][4] = Math.max(dp[i-1][3]+prices[i-1],dp[i-1][4]); } return dp[prices.length][4]; } }

day96

152. 乘积最大子数组

• 题目

  给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续子数组（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

  测试用例的答案是一个 32-位 整数。

  子数组 是数组的连续子序列。

  示例 1:

  1 2 3

  输入: nums = [2,3,-2,4] 输出: 6 解释: 子数组 [2,3] 有最大乘积 6。

  示例 2:

  1 2 3

  输入: nums = [-2,0,-1] 输出: 0 解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

  提示:

  • 1 <= nums.length <= 2 * 104
  • -10 <= nums[i] <= 10
  • nums 的任何前缀或后缀的乘积都 保证 是一个 32-位 整数

• 解法

  方法一：数学规律

  依题意不难看出：我们可以顺序连乘，直到遇到0时，我们需要重新连乘。每次连乘都要找到最大的乘积。我们需要正向和反向两个操作才能把所有组合全部遍历一遍。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  class Solution { public int maxProduct(int[] nums) { int ans = 1; int max = Integer.MIN_VALUE; if(nums.length==1) return nums[0]; // 正向求最大 for(int i=0;i<nums.length;i++){ if(nums[i]==0){ ans=1; continue; } ans*=nums[i]; if(ans>max){ max = ans; } } // 反向求最大 ans = 1; for(int i=nums.length-1;i>=0;i--){ if(nums[i]==0){ ans=1; continue; } ans*=nums[i]; if(ans>max){ max = ans; } } return max>0?max:0; } }

  方法二：动态规划

day97

416. 分割等和子集

• 题目

  给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

  示例 1：

  1 2 3

  输入：nums = [1,5,11,5] 输出：true 解释：数组可以分割成 [1, 5, 5] 和 [11] 。

  示例 2：

  1 2 3

  输入：nums = [1,2,3,5] 输出：false 解释：数组不能分割成两个元素和相等的子集。

  提示：

  • 1 <= nums.length <= 200
  • 1 <= nums[i] <= 100

• 解法

  每个元素只可以被选择1次，就是01背包问题 背包容量为sum/2，也就是在nums里挑选出刚好装满背包可能性

  01背包的应用

  二维DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public boolean canPartition(int[] nums) { if(nums.length<=1) return false; int sum = 0; for(int v:nums) sum+=v; if(sum%2!=0) return false; int bag = sum/2;// 背包容量 // 定义状态：dp[i][j]表示放入前i个物品时，是否可以凑出容量j boolean[][] dp = new boolean[nums.length+1][bag+1]; // 初始化 dp[0][0] = true; for(int i=1;i<=nums.length;i++){ for(int j=0;j<=bag;j++){ if(j>=nums[i-1]) dp[i][j] = dp[i-1][j]||dp[i-1][j-nums[i-1]]; else dp[i][j] = dp[i-1][j]; } } return dp[nums.length][bag]; } }

  滚动数组优化二维DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public boolean canPartition(int[] nums) { if(nums.length<=1) return false; int sum = 0; for(int v:nums) sum+=v; if(sum%2!=0) return false; int bag = sum/2;// 背包容量 // 定义状态：dp[j]表示是否可以凑出容量j boolean[] dp = new boolean[bag+1]; // 初始化 dp[0] = true; // 注意一维dp为了避免状态转移过程中状态的覆盖。需要先遍历物品再遍历背包； // 而且由于物品只放入一次，所以背包需要倒序遍历，否则就会放入多次物品，那这就不是01背包了，而是完全背包 for(int i=1;i<=nums.length;i++){ for(int j=bag;j>=0;j--){ if(j>=nums[i-1]) dp[j] = dp[j]||dp[j-nums[i-1]]; } } return dp[bag]; } }

  背包倒序遍历的解释：

  需要倒序遍历背包容量。如果是顺序放入，那么根据dp转移方程： 第j个状态可能是由前面的第j-w[i]个状态转移过来。 如果顺序遍历，那么就会先算出前面的值，算出前面的值过后，后面dp转移的时候又可能会用到， 那么也就是说，一个物品被放入了多次。这就不是01背包问题了，而是完全背包

day98

474. 一和零

• 题目

  给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

  请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

  如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

  示例 1：

  1 2 3 4

  输入：strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3 输出：4 解释：最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ，因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

  示例 2：

  1 2 3

  输入：strs = ["10", "0", "1"], m = 1, n = 1 输出：2 解释：最大的子集是 {"0", "1"} ，所以答案是 2 。

  提示：

  • 1 <= strs.length <= 600
  • 1 <= strs[i].length <= 100
  • strs[i] 仅由 '0' 和 '1' 组成
  • 1 <= m, n <= 100

• 解法

  解法一：01背包的变种

  https://leetcode.cn/problems/ones-and-zeroes/solution/yi-he-ling-by-leetcode-solution-u2z2/

  二维DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

  class Solution { public int findMaxForm(String[] strs, int m, int n) { // 统计1的个数 int[] ones = new int[strs.length]; int count = 0; for(int i=0;i<strs.length;i++){ for(int j=0;j<strs[i].length();j++){ if(strs[i].charAt(j)=='1') count++; } ones[i] = count; count = 0; } // 定义dp: 表示选择的字符串个数 int[][][] dp = new int[strs.length+1][m+1][n+1]; // 初始化状态：当i==0时，表示取零个串，当然dp[0][][] = 0 // 状态转移: 完全就是01背包问题，只不过背包的维度增加了。 for(int i=1;i<=strs.length;i++){ for(int j=m;j>=0;j--){ for(int k=n;k>=0;k--){ int a = strs[i-1].length()-ones[i-1]; int b = ones[i-1]; if(j>=a&&k>=b){ dp[i][j][k] = Math.max(dp[i-1][j][k],dp[i-1][j-a][k-b]+1); }else{ dp[i][j][k] = dp[i-1][j][k]; } } } } return dp[strs.length][m][n]; } }

  滚动数组优化为一维DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  class Solution { public int findMaxForm(String[] strs, int m, int n) { // 统计1的个数 int[] ones = new int[strs.length]; int count = 0; for(int i=0;i<strs.length;i++){ for(int j=0;j<strs[i].length();j++){ if(strs[i].charAt(j)=='1') count++; } ones[i] = count; count = 0; } // 定义dp: 表示选择的字符串个数 int[][] dp = new int[m+1][n+1]; // 初始化状态：为0 // 状态转移 for(int i=1;i<=strs.length;i++){ for(int j=m;j>=0;j--){// 倒序 for(int k=n;k>=0;k--){// 倒序 int a = strs[i-1].length()-ones[i-1]; int b = ones[i-1]; if(j>=a&&k>=b){ dp[j][k] = Math.max(dp[j][k],dp[j-a][k-b]+1); } } } } return dp[m][n]; } }

day99

494. 目标和

• 题目

  给你一个整数数组 nums 和一个整数 target 。

  向数组中的每个整数前添加 '+' 或 '-' ，然后串联起所有整数，可以构造一个 表达式 ：

  • 例如，nums = [2, 1] ，可以在 2 之前添加 '+' ，在 1 之前添加 '-' ，然后串联起来得到表达式 "+2-1" 。

  返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

  示例 1：

  1 2 3 4 5 6 7 8

  输入：nums = [1,1,1,1,1], target = 3 输出：5 解释：一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3

  示例 2：

  1 2	输入：nums = [1], target = 1 输出：1

  提示：

  • 1 <= nums.length <= 20
  • 0 <= nums[i] <= 1000
  • 0 <= sum(nums[i]) <= 1000
  • -1000 <= target <= 1000

• 解法

  方法一：DFS

  暴力DFS搜索所有解空间即可

  1 2 3 4 5 6 7 8 9 10 11 12 13

  class Solution { public int findTargetSumWays(int[] nums, int target) { return dfs(nums,target,0,0); } public int dfs(int[] nums, int target,int i,int next){ if(i==nums.length){ if(next==target) return 1; return 0; } return dfs(nums,target,i+1,next+nums[i])+dfs(nums,target,i+1,next-nums[i]); } }

  方法二：DP

  https://leetcode.cn/problems/target-sum/solution/mu-biao-he-by-leetcode-solution-o0cp/

  将nums分成两堆数字（s1,s2），使得这两堆数字的差值等于target s1-s2=target s1+s2=sum 2*s1 = sum+target s1 = (sum+target)/2 s2 = (sum-target)/2 也就是说需要分出一堆数字为和为s1或s2的堆 将问题转化为为了背包问题 这里的话还是选择填充容量为s2的背包 因为选择s1的背包的话，如果要求的target为负数的话，数组的索引初始化会溢出

  二维DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  class Solution { public int findTargetSumWays(int[] nums, int target) { if(nums.length<=1) return nums[0]==Math.abs(target)?1:0; int sum = 0; for(int v:nums) sum+=v; if((sum-target)%2!=0||target>sum) return 0; int bag = Math.abs((sum-target))/2; // 状态表示：dp[i][j]表示取第i个数后j容量背包的方法总数 int[][] dp = new int[nums.length+1][bag+1]; // 初始化 dp[0][0] = 1; // 状态转移 for(int i=1;i<=nums.length;i++){ for(int j=0;j<=bag;j++){ if(j>=nums[i-1]){ dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]]; }else if(j<nums[i-1]){ // 放不下，方法数不变 dp[i][j] = dp[i-1][j]; } } } return dp[nums.length][bag]; } }

  滚动数组优化为一维DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public int findTargetSumWays(int[] nums, int target) { if(nums.length<=1) return nums[0]==Math.abs(target)?1:0; int sum = 0; for(int v:nums) sum+=v; if((sum-target)%2!=0||target>sum) return 0; int bag = Math.abs((sum-target))/2; // 状态表示：dp[i][j]表示取第i个数后j容量背包的方法总数 int[] dp = new int[bag+1]; // 初始化 dp[0] = 1; // 状态转移 for(int i=1;i<=nums.length;i++){ for(int j=bag;j>=0;j--){// 倒序避免状态的覆盖，从而造成01背包，避免完全背包 if(j>=nums[i-1]){ dp[j] = dp[j] + dp[j-nums[i-1]]; } } } return dp[bag]; } }

day100

1049. 最后一块石头的重量 II

• 题目

  有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

  每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

  • 如果 x == y，那么两块石头都会被完全粉碎；
  • 如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

  最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

  示例 1：

  1 2 3 4 5 6 7

  输入：stones = [2,7,4,1,8,1] 输出：1 解释： 组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]， 组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]， 组合 2 和 1，得到 1，所以数组转化为 [1,1,1]， 组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

  示例 2：

  1 2	输入：stones = [31,26,33,21,40] 输出：5

  提示：

  • 1 <= stones.length <= 30
  • 1 <= stones[i] <= 100

• 解法

  方法一：动态规划

  https://leetcode.cn/problems/last-stone-weight-ii/solution/zui-hou-yi-kuai-shi-tou-de-zhong-liang-i-95p9/

  二维DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { public int lastStoneWeightII(int[] stones) { if(stones.length<=1) return stones[0]; int sum = 0; for(int v:stones) sum+=v; int bag = sum/2;// 直接向下取整 // 状态表示：dp[i][j]表示选取前i个石头，容量为j时，能放入的最大重量 int[][] dp = new int[stones.length][bag+1]; // 初始化 //dp[i][0] = 0; // dp[0][j] = stones[0]; 初始化i=0时的情况，装得下就可以取第0个石头 for(int j=0;j<=bag;j++){ if(j>=stones[0]){ dp[0][j] = stones[0]; } } for(int i=1;i<stones.length;i++){ for(int j=1;j<=bag;j++){ if(j>=stones[i]) dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-stones[i]]+stones[i]); else dp[i][j] = dp[i-1][j]; } } // System.out.println(Arrays.deepToString(dp)); return sum-2*dp[stones.length-1][bag]; } } // 将石头分成总重量最接近的两堆，这样碰撞后可以得到最小的堆 // 也就是要在一堆石头里找到可以最接近sum的half堆

  滚动数组优化的DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

  class Solution { public int lastStoneWeightII(int[] stones) { if(stones.length<=1) return stones[0]; int sum = 0; for(int v:stones) sum+=v; int bag = sum/2;// 直接向下取整 // 状态表示：dp[j]表示选取容量为j时，能放入的最大重量 int[] dp = new int[bag+1]; // 初始化 dp[0] = 0; // 初始化从0开始，因为第一行还没被填写 for(int i=0;i<stones.length;i++){ for(int j=bag;j>=stones[i];j--){// 倒序 if(j>=stones[i]) dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i]); } } // System.out.println(Arrays.deepToString(dp)); return sum-2*dp[bag]; } }

day101

139. 单词拆分

• 题目

  给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

  **注意：**不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

  示例 1：

  1 2 3

  输入: s = "leetcode", wordDict = ["leet", "code"] 输出: true 解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。

  示例 2：

  1 2 3 4

  输入: s = "applepenapple", wordDict = ["apple", "pen"] 输出: true 解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。 注意，你可以重复使用字典中的单词。

  示例 3：

  1 2	输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"] 输出: false

  提示：

  • 1 <= s.length <= 300
  • 1 <= wordDict.length <= 1000
  • 1 <= wordDict[i].length <= 20
  • s 和 wordDict[i] 仅有小写英文字母组成
  • wordDict 中的所有字符串 互不相同

• 解法

  解法一：DP

  https://leetcode.cn/problems/word-break/solution/dan-ci-chai-fen-by-leetcode-solution/

day102

279. 完全平方数

• 题目

  给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

  完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

  示例 1：

  1 2 3

  输入：n = 12 输出：3 解释：12 = 4 + 4 + 4

  示例 2：

  1 2 3

  输入：n = 13 输出：2 解释：13 = 4 + 9

  提示：

  • 1 <= n <= 104

• 解法

  解法一：DP

  https://leetcode.cn/problems/perfect-squares/solution/wan-quan-ping-fang-shu-by-leetcode-solut-t99c/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

  class Solution { public int numSquares(int n) { // dp[i][j]表示选取前i个完全平方数，和为j时的所选完全平方数最少数量 int num = 1; for(;num<n;num++){ if(num*num>=n) break; } int[][] dp = new int[num+1][n+1]; // 初始化：毫无疑问，求得最小值，为了避免初始状态的覆盖，需要初始化为n+1，因为最多的情况就是n个1 for(int[] one:dp) Arrays.fill(one,n+1); // 开始 dp[0][0] = 0; for(int i=1;i<=num;i++){ for(int j=0;j<=n;j++){ if(j>=i*i) dp[i][j] = Math.min(dp[i-1][j],dp[i][j-i*i]+1); else dp[i][j] = dp[i-1][j]; } } // System.out.println(Arrays.deepToString(dp)); return dp[num][n]; } }

  优化DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public int numSquares(int n) { // dp[j]表示所选完全平方数和为j时的最少数量 int num = 1; for(;num<n;num++){ if(num*num>=n) break; } int[] dp = new int[n+1]; // 初始化：毫无疑问，求得最小值，为了避免初始状态的覆盖，需要初始化为n+1，因为最多的情况就是n个1 Arrays.fill(dp,n+1); // 开始 dp[0] = 0; for(int i=1;i<=num;i++){ for(int j=0;j<=n;j++){ if(j>=i*i) dp[j] = Math.min(dp[j],dp[j-i*i]+1); } } // System.out.println(Arrays.toString(dp)); return dp[n]; } }

day103

322. 零钱兑换

• 题目

  给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

  计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

  你可以认为每种硬币的数量是无限的。

  示例 1：

  1 2 3

  输入：coins = [1, 2, 5], amount = 11 输出：3 解释：11 = 5 + 5 + 1

  示例 2：

  1 2	输入：coins = [2], amount = 3 输出：-1

  示例 3：

  1 2	输入：coins = [1], amount = 0 输出：0

  提示：

  • 1 <= coins.length <= 12
  • 1 <= coins[i] <= 231 - 1
  • 0 <= amount <= 104

• 解法

  方法一：记忆化搜索

  方法二：DP

  https://leetcode.cn/problems/coin-change/solution/322-ling-qian-dui-huan-by-leetcode-solution/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  class Solution { public int coinChange(int[] coins, int amount) { // 状态定义：dp[i][j]表示取前i种面额的硬币，容量为j，所需的最少硬币个数 int[][] dp = new int[coins.length + 1][amount + 1]; // 初始状态：因为状态方程是求最小值，所以这里需要初始化一个较大的数即可 // 不然结果全为0.当然初始化也有讲究，不能初始化一个特别大的数如Integer.MAX_VALUE， // 太大的数在状态转移过程中会溢出。我们知道硬币的面值最小是1，那么最多的硬币数量就是面值，所以初始化为面值+1 for (int[] ints : dp) { Arrays.fill(ints,amount+1); } // 注意因为状态转移取得是最小值，所以这里状态初始化，需要初始化为大于amount的数字才行。不然小了。就直接取那个小的数了。显然不正确，因为会被覆盖了 dp[0][0]=0; // 状态转移：如果当前硬币面额可以取出，既可以取也可以不取，取两种方式的最优解 for (int i = 1; i <= coins.length; i++) { for (int j = 0; j <= amount; j++) { if (coins[i - 1] <= j) dp[i][j] = Math.min(dp[i][j - coins[i - 1]] + 1, dp[i - 1][j]); else dp[i][j] = dp[i - 1][j]; } } // System.out.println(Arrays.deepToString(dp)); return dp[coins.length][amount]>amount?-1:dp[coins.length][amount]; } }

  优化DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public int coinChange(int[] coins, int amount) { // dp[j]表示凑出金额j的最少硬币个数 int[] dp = new int[amount+1]; // 初始化 Arrays.fill(dp,amount+1); dp[0]=0; // 状态转移 for(int i=1;i<=coins.length;i++){ for(int j=0;j<=amount;j++){ if(j>=coins[i-1]) dp[j] = Math.min(dp[j],dp[j-coins[i-1]]+1); } } // System.out.println(Arrays.deepToString(dp)); return dp[amount]>amount?-1:dp[amount]; } }

day104

377. 组合总和 Ⅳ

• 题目

  给你一个由 不同 整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。

  题目数据保证答案符合 32 位整数范围。

  示例 1：

  1 2 3 4 5 6 7 8 9 10 11 12

  输入：nums = [1,2,3], target = 4 输出：7 解释： 所有可能的组合为： (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1) 请注意，顺序不同的序列被视作不同的组合。

  示例 2：

  1 2	输入：nums = [9], target = 3 输出：0

  提示：

  • 1 <= nums.length <= 200
  • 1 <= nums[i] <= 1000
  • nums 中的所有元素 互不相同
  • 1 <= target <= 1000

  **进阶：**如果给定的数组中含有负数会发生什么？问题会产生何种变化？如果允许负数出现，需要向题目中添加哪些限制条件？

• 解法

  方法一：记忆化搜索

  方法二：DP

  https://leetcode.cn/problems/combination-sum-iv/solution/zu-he-zong-he-iv-by-leetcode-solution-q8zv/

day105

509. 斐波那契数

• 斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

  1 2	F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n > 1

  给定 n ，请计算 F(n) 。

  示例 1：

  1 2 3

  输入：n = 2 输出：1 解释：F(2) = F(1) + F(0) = 1 + 0 = 1

  示例 2：

  1 2 3

  输入：n = 3 输出：2 解释：F(3) = F(2) + F(1) = 1 + 1 = 2

  示例 3：

  1 2 3

  输入：n = 4 输出：3 解释：F(4) = F(3) + F(2) = 2 + 1 = 3

  提示：

  • 0 <= n <= 30

• 解法

  方法一：DFS暴搜

  斐波那契数的定义很符合递归函数，因此比较容易写出递归函数写法

  1 2 3 4 5 6

  class Solution { public int fib(int n) { if(n<=1) return n; return fib(n-1)+fib(n-2); } }

  方法二：DFS+记忆化搜索

  方法一还可以改进一下。我们很容易知道：斐波那契数是不断往两个分支递归，这样会出现一些数字的重复计算。我们可以在递归的过程中将这些数据记录下来，下次要用时，直接拿出来用即可，避免多余的递归。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

  class Solution { public int fib(int n) { int[] history = new int[n]; return dfs(n,history,0); } public int dfs(int n,int[] history,int i){ if(n<=1) return n; // 有记录，则直接拿 if(history[i]!=0) return history[i]; // 没有记录，需要计算 else { history[i] = fib(n-1)+fib(n-2); return history[i]; } } }

  方法三：DP

  这道题也容易想到动态规划的解法，因为题目的定义看着就很动态规划，状态转移方程已经很显然地给出了。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

  class Solution { public int fib(int n) { if(n<=1) return n; // 状态表示：dp[i]表示第i个斐波那契数 int[] dp = new int[n+1]; // 初始化dp dp[0] = 0; dp[1] = 1; for(int i=2;i<=n;i++){ dp[i] = dp[i-1] + dp[i-2]; } return dp[n]; } } // 由于当前状态只与前两个状态有关，所以可以利用滚动数组地思想优化为常数空间复杂度

day106

746. 使用最小花费爬楼梯

• 题目

  给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。

  你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。

  请你计算并返回达到楼梯顶部的最低花费。

  示例 1：

  1 2 3 4 5

  输入：cost = [10,15,20] 输出：15 解释：你将从下标为 1 的台阶开始。 - 支付 15 ，向上爬两个台阶，到达楼梯顶部。 总花费为 15 。

  示例 2：

  1 2 3 4 5 6 7 8 9 10

  输入：cost = [1,100,1,1,1,100,1,1,100,1] 输出：6 解释：你将从下标为 0 的台阶开始。 - 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。 - 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。 - 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。 - 支付 1 ，向上爬一个台阶，到达楼梯顶部。 总花费为 6 。

  提示：

  • 2 <= cost.length <= 1000
  • 0 <= cost[i] <= 999

• 解法

  方法一：DP

  https://leetcode.cn/problems/min-cost-climbing-stairs/solution/shi-yong-zui-xiao-hua-fei-pa-lou-ti-by-l-ncf8/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public int minCostClimbingStairs(int[] cost) { // 状态定义：dp[i]表示爬到第i阶台阶的最低花费 int[] dp = new int[cost.length+1]; // 状态初始化：题目说可以直接不花费任何费用到达1或0 dp[0] = 0; dp[1] = 0; // 状态转移方程：dp[i]状态是由dp[i-1]或dp[i-2]转移过来，选择费用最低的方案即可 for(int i=2;i<dp.length;i++){ dp[i] = Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]); } // System.out.println(Arrays.toString(dp)); return dp[cost.length]; } }

day107

17. 电话号码的字母组合

• 题目

  给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

  给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

  

  示例 1：

  1 2	输入：digits = "23" 输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

  示例 2：

  1 2	输入：digits = "" 输出：[]

  示例 3：

  1 2	输入：digits = "2" 输出：["a","b","c"]

  提示：

  • 0 <= digits.length <= 4
  • digits[i] 是范围 ['2', '9'] 的一个数字。

• 解法

  本题很容易想到DFS暴力搜索的方法，再加上题目给的数据集很小，所以DFS暴力搜索可以解决。依据题目输入digits字符串，找到其中每个数字字符匹配的一个字符之后再组合即是答案，于是，就可以不断地遍历digits，去搜索所有的字符情况，当然需要注意回溯。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

  class Solution { String[] ss; public List<String> letterCombinations(String digits) { ss = new String[]{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"}; List<String> ls = new ArrayList<>(); if(digits.length()==0) { return ls; } dfs(digits,digits.length(),"",ls); return ls; } public void dfs(String digits,int step,String ans,List<String> ls){ // 结束条件 if(step==0){ // System.out.println(ans); ls.add(ans); return; } // 开始放第sIdx个位置 int sIdx = Integer.parseInt(Character.toString(digits.charAt(digits.length()-step)),10); for(int j=0;j<ss[sIdx].length();j++){ // 先取第一个 ans+= ss[sIdx].charAt(j); dfs(digits,step-1,ans,ls); // 回溯到上一层 ans = ans.substring(0,ans.length()-1); } } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  func letterCombinations(digits string) []string { if len(digits) == 0 { return []string{} } table:=[]string{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"} return dfs(table,digits,0,"") } func dfs(table []string, digits string, step int, cur string) []string { if step == len(digits){ return []string{cur} } ans := []string{} // 依次取号 didx,_:=strconv.Atoi(string(digits[step])) // 遍历号对应所有字符 for i:=0;i<len(table[didx]);i++{ cur+=string(table[didx][i]) ans = append(ans,dfs(table,digits,step+1,cur)...) cur = string(cur[:len(cur)-1]) } return ans }

day108

22. 括号生成

• 题目

  数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

  示例 1：

  1 2	输入：n = 3 输出：["((()))","(()())","(())()","()(())","()()()"]

  示例 2：

  1 2	输入：n = 1 输出：["()"]

  提示：

  • 1 <= n <= 8

• 解法

  官方解法：暴力与回溯

  我这里的解法是暴力回溯。其实这个问题也是属于组合问题，但是组合是有条件限制的。必须满足括号匹配原则的组合才能追加到最后的结果里。那么我们怎样判断呢？

  可以通过栈这种数据结构来实现括号匹配：当栈空的时候就往里面加括号，如果非空，就看栈顶的括号与即将加入的括号是否配对，配对就pop掉栈顶的括号，否则就加入到栈中。最后如果栈空了，就表明括号匹配，否则不能追加到结果里。

  当然，其实这个过程可以优化一下：没必要等到所有括号处理完毕再判断，其实中间过程就可以提前判断出来，终止继续深度递归了，可以在一定程度优化时间复杂度。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46

  // 先dfs放下所有组合，然后用栈来判断dfs的过程是否合理 class Solution { String[] table; public Solution(){ table = new String[]{"(",")"}; } public List<String> generateParenthesis(int n) { List<String> list = new ArrayList<>(); Stack<String> st = new Stack<>(); dfs(list,0,n,"",st); return list; } public void dfs(List<String> list,int step,int n,String ans,Stack<String> st){ if(step==2*n){ if(st.empty()) list.add(ans); return; } for(int i=0;i<2;i++){ // 在放括号之前，需要保证括号配对 // 下面的变量用来记录当前深度的值，方便回溯 boolean op=false; String tmp =""; if(st.empty()){ st.push(table[i]); }else{ if(table[i]==")"&&st.peek()=="("){ tmp = st.pop(); op = true; }else{ st.push(table[i]); } } ans+=table[i]; dfs(list,step+1,n,ans,st); // 注意：这里借助栈来判断是否括号配对的同时也是dfs，所以需要注意回溯 ans = ans.substring(0,ans.length()-1); if(!op){ st.pop(); }else{ st.push(tmp); } } } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

  func generateParenthesis(n int) []string { stack :=[]byte{} return dfs(stack,"",0,n) } func dfs(stack []byte,cur string,step int,n int) []string{ if step==2*n { if len(stack)==0{ return []string{cur} }else{ return []string{} } } ans := []string{} for i:=0;i<2;i++{ next:=byte('(') if i==1{ next = ')' } flag:=false last :=byte(' ') if len(stack)!=0&&next==')'&&stack[len(stack)-1]=='('{ last = stack[len(stack)-1] stack = stack[:len(stack)-1] }else{ stack = append(stack,next) flag = true } ans = append(ans,dfs(stack,cur+string(next),step+1,n)...) // 回溯 栈 if flag{ stack = stack[:len(stack)-1] }else{ stack = append(stack,last) } } return ans }

day109

39. 组合总和

• 题目

  给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

  candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

  对于给定的输入，保证和为 target 的不同组合数少于 150 个。

  示例 1：

  1 2 3 4 5 6

  输入：candidates = [2,3,6,7], target = 7 输出：[[2,2,3],[7]] 解释： 2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。 7 也是一个候选， 7 = 7 。 仅有这两种组合。

  示例 2：

  1 2	输入: candidates = [2,3,5], target = 8 输出: [[2,2,2,2],[2,3,3],[3,5]]

  示例 3：

  1 2	输入: candidates = [2], target = 1 输出: []

  提示：

  • 1 <= candidates.length <= 30
  • 2 <= candidates[i] <= 40
  • candidates 的所有元素 互不相同
  • 1 <= target <= 40

• 解法

  题解

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90

  import java.util.ArrayDeque; import java.util.ArrayList; import java.util.Deque; import java.util.List; public class Solution { public List<List<Integer>> combinationSum(int[] candidates, int target) { int len = candidates.length; List<List<Integer>> res = new ArrayList<>(); if (len == 0) { return res; } Deque<Integer> path = new ArrayDeque<>(); dfs(candidates, 0, len, target, path, res); return res; } /** * @param candidates 候选数组 * @param begin 搜索起点 * @param len 冗余变量，是 candidates 里的属性，可以不传 * @param target 每减去一个元素，目标值变小 * @param path 从根结点到叶子结点的路径，是一个栈 * @param res 结果集列表 */ private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) { // target 为负数和 0 的时候不再产生新的孩子结点 if (target < 0) { return; } if (target == 0) { res.add(new ArrayList<>(path)); return; } // 重点理解这里从 begin 开始搜索的语意 for (int i = begin; i < len; i++) { path.addLast(candidates[i]); // 注意：由于每一个元素可以重复使用，下一轮搜索的起点依然是i，这里非常容易弄错 dfs(candidates, i, len, target - candidates[i], path, res); // 状态重置 path.removeLast(); } } } // 剪枝优化版 import java.util.ArrayDeque; import java.util.ArrayList; import java.util.Arrays; import java.util.Deque; import java.util.List; public class Solution { public List<List<Integer>> combinationSum(int[] candidates, int target) { int len = candidates.length; List<List<Integer>> res = new ArrayList<>(); if (len == 0) { return res; } // 排序是剪枝的前提 Arrays.sort(candidates); Deque<Integer> path = new ArrayDeque<>(); dfs(candidates, 0, len, target, path, res); return res; } private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) { // 由于进入更深层的时候，小于 0 的部分被剪枝，因此递归终止条件值只判断等于 0 的情况 if (target == 0) { res.add(new ArrayList<>(path)); return; } for (int i = begin; i < len; i++) { // 重点理解这里剪枝，前提是候选数组已经有序 // 已经为负数了，没有必要再搜索下去了，提前结束 if (target - candidates[i] < 0) { break; } path.addLast(candidates[i]); dfs(candidates, i, len, target - candidates[i], path, res); path.removeLast(); } } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

  func combinationSum(candidates []int, target int) [][]int { ans := [][]int{} var dfs func(candidates, subs []int, target, step int) dfs = func(candidates, subs []int, target, step int) { if target < 0 { return } tmp := make([]int, len(subs)) if target == 0 { copy(tmp, subs) ans = append(ans, tmp) return } for i := step; i < len(candidates); i++ { subs = append(subs, candidates[i]) dfs(candidates, subs, target-candidates[i], i) subs = subs[:len(subs)-1] } return } dfs(candidates, []int{}, target, 0) return ans }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27

  // 剪枝优化版 func combinationSum(candidates []int, target int) [][]int { ans := [][]int{} var dfs func(candidates, subs []int, target, step int) dfs = func(candidates, subs []int, target, step int) { tmp := make([]int, len(subs)) if target == 0 { copy(tmp, subs) ans = append(ans, tmp) return } for i := step; i < len(candidates); i++ { if target-candidates[i]<0{ break } subs = append(subs, candidates[i]) dfs(candidates, subs, target-candidates[i], i) subs = subs[:len(subs)-1] } return } sort.Ints(candidates) dfs(candidates, []int{}, target, 0) return ans }

day110

78. 子集

• 题目

  给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

  解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

  示例 1：

  1 2	输入：nums = [1,2,3] 输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

  示例 2：

  1 2	输入：nums = [0] 输出：[[],[0]]

  提示：

  • 1 <= nums.length <= 10
  • -10 <= nums[i] <= 10
  • nums 中的所有元素 互不相同

• 解法

  DFS

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  class Solution { public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> lls = new ArrayList<>(); List<Integer> ls = new ArrayList<>(); dfs(lls,ls,nums,0); return lls; } public void dfs(List<List<Integer>> lls,List<Integer> ls,int[] nums,int step){ if(step==nums.length){ lls.add(new ArrayList<>(ls)); return; } // System.out.println(ls.toString()); ls.add(ls.size(),nums[step]); // System.out.println("递归前："+ls.toString()); // 取下一个数 dfs(lls,ls,nums,step+1); // System.out.println("递归后："+ls.toString()); // 回溯 ls.remove(ls.size()-1); // 直接取下一个数，不取当前数 dfs(lls,ls,nums,step+1); } }

day111

343. 整数拆分

• 题目

  给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

  返回 你可以获得的最大乘积 。

  示例 1:

  1 2 3

  输入: n = 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1。

  示例 2:

  1 2 3

  输入: n = 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

  提示:

  • 2 <= n <= 58

• 解法

  代码随想录–dp

  官方题解

day112

96. 不同的二叉搜索树

• 题目

  给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

  示例 1：

  

  1 2	输入：n = 3 输出：5

  示例 2：

  1 2	输入：n = 1 输出：1

  提示：

  • 1 <= n <= 19

• 解法

  相比官方更容易看懂得解法

  官方题解

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  func numTrees(n int) int { if n==0 || n==1{ return 1 } if c,ok:=m[n];ok{ return c } count:=0 for i:=1;i<=n;i++{ l:=numTrees(i-1) r:=numTrees(n-i) count += l*r } m[n]=count return count } // 记忆化 var m = map[int]int{}

day113

518. 零钱兑换 II

• 题目

  给你一个整数数组 coins 表示不同面额的硬币，另给一个整数 amount 表示总金额。

  请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额，返回 0 。

  假设每一种面额的硬币有无限个。

  题目数据保证结果符合 32 位带符号整数。

  示例 1：

  1 2 3 4 5 6 7

  输入：amount = 5, coins = [1, 2, 5] 输出：4 解释：有四种方式可以凑成总金额： 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1

  示例 2：

  1 2 3

  输入：amount = 3, coins = [2] 输出：0 解释：只用面额 2 的硬币不能凑成总金额 3 。

  示例 3：

  1 2	输入：amount = 10, coins = [10] 输出：1

  提示：

  • 1 <= coins.length <= 300
  • 1 <= coins[i] <= 5000
  • coins 中的所有值 互不相同
  • 0 <= amount <= 5000

• 解法

  二维DP

  典型的完全背包问题，需要注意：这里的背包容量需要正序遍历，因为状态转移方程是不断地去拿左上角的值，我们要确保这个值肯定要被算过（这样才符合完全背包的定义）。所以需要正序遍历背包容量。

  状态转移方程也有不同

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public int change(int amount, int[] coins) { // 状态定义：dp[i][j]表示取1-i种硬币时，可以凑出面额为j的方法有多少种 int[][] dp = new int[coins.length+1][amount+1]; // 初始化：没有拿硬币时，可以凑出0的面额，方法有1种，就是什么都不做 dp[0][0] = 1; // 状态转移 for(int i=1;i<=coins.length;i++){ for(int j=0;j<=amount;j++){ if(j>=coins[i-1]) dp[i][j] = dp[i-1][j] + dp[i][j-coins[i-1]]; else dp[i][j] = dp[i-1][j]; } } // System.out.println(Arrays.deepToString(dp)); return dp[coins.length][amount]; } }

  滚动数组优化为一维DP

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public int change(int amount, int[] coins) { // 状态定义：dp[i]可以凑出面额为i的方法有多少种 int[] dp = new int[amount+1]; // 初始化：没有拿硬币时，可以凑出0的面额，方法有1种，就是什么都不做 dp[0] = 1; // 状态转移 for(int i=1;i<=coins.length;i++){ for(int j=coins[i-1];j<=amount;j++){// 枚举背包容量，当然最小肯定就是cons[i-1]了 if(j>=coins[i-1]) dp[j] = dp[j] + dp[j-coins[i-1]]; } } // System.out.println(Arrays.roString(dp)); return dp[amount]; } }

day114

多重背包

• 题目

  有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量，且价值总和最大。

• 解法

  多重背包和01背包是非常像的， 为什么和01背包像呢？

  每件物品最多有Mi件可用，把Mi件摊开，其实就是一个01背包问题了。

  例如：

  背包最大重量为10。

  物品为：

  	重量	价值	数量
  物品0	1	15	2
  物品1	3	20	3
  物品2	4	30	2

  问背包能背的物品最大价值是多少？

  和如下情况有区别么？

  	重量	价值	数量
  物品0	1	15	1
  物品0	1	15	1
  物品1	3	20	1
  物品1	3	20	1
  物品1	3	20	1
  物品2	4	30	1
  物品2	4	30	1

  毫无区别，这就转成了一个01背包问题了，且每个物品只用一次。

  • 时间复杂度：O(m × n × k)，m：物品种类个数，n背包容量，k单类物品数量

  也有另一种实现方式，就是把每种商品遍历的个数放在01背包里面在遍历一遍。

  毫无区别，这就转成了一个01背包问题了，且每个物品只用一次。

  • 时间复杂度：O(m × n × k)，m：物品种类个数，n背包容量，k单类物品数量

  从代码里可以看出是01背包里面在加一个for循环遍历一个每种商品的数量。 和01背包还是如出一辙的。

  当然还有那种二进制优化的方法，其实就是把每种物品的数量，打包成一个个独立的包。

  和以上在循环遍历上有所不同，因为是分拆为各个包最后可以组成一个完整背包，具体原理我就不做过多解释了，大家了解一下就行，面试的话基本不会考完这个深度了，感兴趣可以自己深入研究一波。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42

  public void testMultiPack1(){ // 版本一：改变物品数量为01背包格式 List<Integer> weight = new ArrayList<>(Arrays.asList(1, 3, 4)); List<Integer> value = new ArrayList<>(Arrays.asList(15, 20, 30)); List<Integer> nums = new ArrayList<>(Arrays.asList(2, 3, 2)); int bagWeight = 10; for (int i = 0; i < nums.size(); i++) { while (nums.get(i) > 1) { // 把物品展开为i weight.add(weight.get(i)); value.add(value.get(i)); nums.set(i, nums.get(i) - 1); } } int[] dp = new int[bagWeight + 1]; for(int i = 0; i < weight.size(); i++) { // 遍历物品 for(int j = bagWeight; j >= weight.get(i); j--) { // 遍历背包容量 dp[j] = Math.max(dp[j], dp[j - weight.get(i)] + value.get(i)); } System.out.println(Arrays.toString(dp)); } } public void testMultiPack2(){ // 版本二：改变遍历个数 int[] weight = new int[] {1, 3, 4}; int[] value = new int[] {15, 20, 30}; int[] nums = new int[] {2, 3, 2}; int bagWeight = 10; int[] dp = new int[bagWeight + 1]; for(int i = 0; i < weight.length; i++) { // 遍历物品 for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量 // 以上为01背包，然后加一个遍历个数 for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数 dp[j] = Math.max(dp[j], dp[j - k * weight[i]] + k * value[i]); } System.out.println(Arrays.toString(dp)); } } }

day115

198. 打家劫舍

• 题目

  你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

  给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

  示例 1：

  1 2 3 4

  输入：[1,2,3,1] 输出：4 解释：偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。 偷窃到的最高金额 = 1 + 3 = 4 。

  示例 2：

  1 2 3 4

  输入：[2,7,9,3,1] 输出：12 解释：偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。 偷窃到的最高金额 = 2 + 9 + 1 = 12 。

  提示：

  • 1 <= nums.length <= 100
  • 0 <= nums[i] <= 400

• 解法

  dp

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  class Solution { public int rob(int[] nums) { // dp[i]表示偷窃前i个房屋，得到的最高金额为多少 int[] dp = new int[nums.length+1]; // 初始化 dp[0] = 0; dp[1] = nums[0]; for(int i=2;i<=nums.length;i++){ dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i-1]); } //System.out.println(Arrays.toString(dp)); return dp[nums.length]; } }

day116

213. 打家劫舍 II

• 题目

  你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

  给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

  示例 1：

  1 2 3

  输入：nums = [2,3,2] 输出：3 解释：你不能先偷窃 1 号房屋（金额 = 2），然后偷窃 3 号房屋（金额 = 2）, 因为他们是相邻的。

  示例 2：

  1 2 3 4

  输入：nums = [1,2,3,1] 输出：4 解释：你可以先偷窃 1 号房屋（金额 = 1），然后偷窃 3 号房屋（金额 = 3）。 偷窃到的最高金额 = 1 + 3 = 4 。

  示例 3：

  1 2	输入：nums = [1,2,3] 输出：3

  提示：

  • 1 <= nums.length <= 100
  • 0 <= nums[i] <= 1000

• 解法

  dp

  这道题目和198.打家劫舍 (opens new window)是差不多的，唯一区别就是成环了。

  对于一个数组，成环的话主要有如下三种情况：

  • 情况一：考虑不包含首尾元素

  

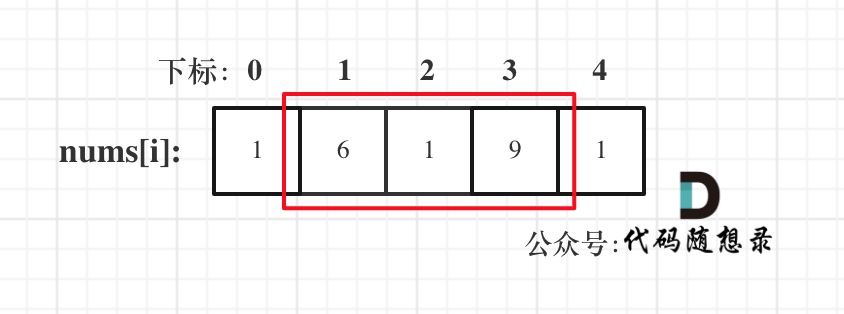
  • 情况二：考虑包含首元素，不包含尾元素

  

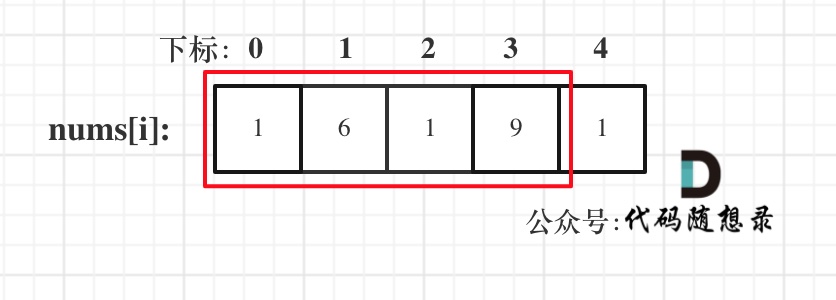
  • 情况三：考虑包含尾元素，不包含首元素

  

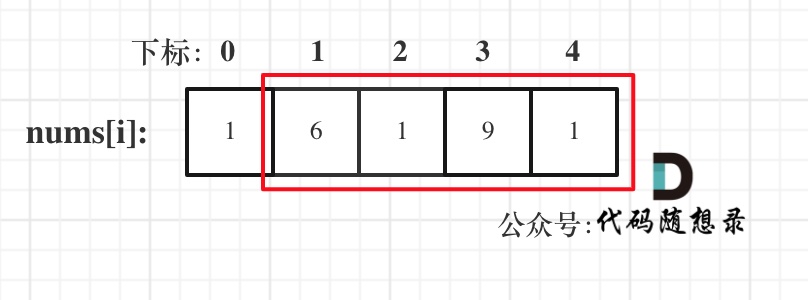
  注意我这里用的是"考虑"，例如情况三，虽然是考虑包含尾元素，但不一定要选尾部元素！ 对于情况三，取nums[1] 和 nums[3]就是最大的。

  而情况二 和 情况三 都包含了情况一了，所以只考虑情况二和情况三就可以了。

  分析到这里，本题其实比较简单了。 剩下的和198.打家劫舍 (opens new window)就是一样的了。

day117

337. 打家劫舍 III

• 题目

  小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

  除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

  给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

  示例 1:

  

  1 2 3

  输入: root = [3,2,3,null,3,null,1] 输出: 7 解释: 小偷一晚能够盗取的最高金额 3 + 3 + 1 = 7

  示例 2:

  

  1 2 3

  输入: root = [3,4,5,1,3,null,1] 输出: 9 解释: 小偷一晚能够盗取的最高金额 4 + 5 = 9

  提示：

  • 树的节点数在 [1, 104] 范围内
  • 0 <= Node.val <= 104

• 解法

  树形dp

day118

188. 买卖股票的最佳时机 IV

• 题目

  给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格，和一个整型 k 。

  设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

  **注意：**你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

  示例 1：

  1 2 3

  输入：k = 2, prices = [2,4,1] 输出：2 解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

  示例 2：

  1 2 3 4

  输入：k = 2, prices = [3,2,6,5,0,3] 输出：7 解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。 随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

  提示：

  • 0 <= k <= 100
  • 0 <= prices.length <= 1000
  • 0 <= prices[i] <= 1000

• 解法

  dp

  思路是"买卖股票最大利润Ⅲ"的变形思维。在原来基础上，由5个状态变为2*k+1个状态，遵循先买后卖原则，找到最大利润

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public int maxProfit(int k, int[] prices) { int[][] dp = new int[prices.length+1][2*k+1]; // 初始化 dp[0][0] = 0; dp[0][2] =0; for(int i=0;i<2*k+1;i++){ if(i%2==1) dp[0][i] = -prices[0]; } for(int i=1;i<=prices.length;i++){ for(int j=0;j<2*k;j++){ dp[i][1+j] = Math.max(dp[i-1][j]+(int)Math.pow(-1,j+1)*prices[i-1],dp[i-1][1+j]); } } return dp[prices.length][2*k]; } }

day119

300. 最长递增子序列

• 题目

  给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

  子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

  示例 1：

  1 2 3

  输入：nums = [10,9,2,5,3,7,101,18] 输出：4 解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

  示例 2：

  1 2	输入：nums = [0,1,0,3,2,3] 输出：4

  示例 3：

  1 2	输入：nums = [7,7,7,7,7,7,7] 输出：1

  提示：

  • 1 <= nums.length <= 2500
  • -104 <= nums[i] <= 104

  进阶：

  • 你能将算法的时间复杂度降低到 O(n log(n)) 吗?

• 解法

  官方题解

  比较容易想的应该是【贪心+二分搜索】

day120

309. 最佳买卖股票时机含冷冻期

• 题目

  给定一个整数数组prices，其中第 prices[i] 表示第 *i* 天的股票价格 。

  设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

  • 卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

  **注意：**你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

  示例 1:

  1 2 3

  输入: prices = [1,2,3,0,2] 输出: 3 解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

  示例 2:

  1 2	输入: prices = [1] 输出: 0

  提示：

  • 1 <= prices.length <= 5000
  • 0 <= prices[i] <= 1000

• 解法

  dp

day121

516. 最长回文子序列

• 题目

  给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。

  子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。

  示例 1：

  1 2 3

  输入：s = "bbbab" 输出：4 解释：一个可能的最长回文子序列为 "bbbb" 。

  示例 2：

  1 2 3

  输入：s = "cbbd" 输出：2 解释：一个可能的最长回文子序列为 "bb" 。

  提示：

  • 1 <= s.length <= 1000
  • s 仅由小写英文字母组成

• 解法

  dp

  这题的难点主要在于定义状态和找到状态转移方程。

day122

583. 两个字符串的删除操作

• 题目

  给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

  一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

  • 例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。

  两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

  示例 1：

  1 2 3

  输入：text1 = "abcde", text2 = "ace" 输出：3 解释：最长公共子序列是 "ace" ，它的长度为 3 。

  示例 2：

  1 2 3

  输入：text1 = "abc", text2 = "abc" 输出：3 解释：最长公共子序列是 "abc" ，它的长度为 3 。

  示例 3：

  1 2 3

  输入：text1 = "abc", text2 = "def" 输出：0 解释：两个字符串没有公共子序列，返回 0 。

  提示：

  • 1 <= text1.length, text2.length <= 1000
  • text1 和 text2 仅由小写英文字符组成。

• 题解

  可以将问题转化为求解【最长公共子序列问题】.

  dp

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

  class Solution { public int minDistance(String word1, String word2) { int m = word1.length(), n = word2.length(); int[][] dp = new int[m + 1][n + 1]; for (int i = 1; i <= m; i++) { char c1 = word1.charAt(i - 1); for (int j = 1; j <= n; j++) { char c2 = word2.charAt(j - 1); if (c1 == c2) { dp[i][j] = dp[i - 1][j - 1] + 1; } else { dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]); } } } return word1.length()+word2.length()-2*dp[m][n]; } }

day123

1143. 最长公共子序列

• 题目

  给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

  每步 可以删除任意一个字符串中的一个字符。

  示例 1：

  1 2 3

  输入: word1 = "sea", word2 = "eat" 输出: 2 解释: 第一步将 "sea" 变为 "ea" ，第二步将 "eat "变为 "ea"

  示例 2:

  1 2	输入：word1 = "leetcode", word2 = "etco" 输出：4

  提示：

  • 1 <= word1.length, word2.length <= 500
  • word1 和 word2 只包含小写英文字母

• 题解

  dp

day124

647. 回文子串

• 题目

  给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。

  回文字符串 是正着读和倒过来读一样的字符串。

  子字符串 是字符串中的由连续字符组成的一个序列。

  具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。

  示例 1：

  1 2 3

  输入：s = "abc" 输出：3 解释：三个回文子串: "a", "b", "c"

  示例 2：

  1 2 3

  输入：s = "aaa" 输出：6 解释：6个回文子串: "a", "a", "a", "aa", "aa", "aaa"

  提示：

  • 1 <= s.length <= 1000
  • s 由小写英文字母组成

• 解法

  dp+中心拓展

day125

674. 最长连续递增序列

• 问题

  给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

  连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。

  示例 1：

  1 2 3 4

  输入：nums = [1,3,5,4,7] 输出：3 解释：最长连续递增序列是 [1,3,5], 长度为3。 尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

  示例 2：

  1 2 3

  输入：nums = [2,2,2,2,2] 输出：1 解释：最长连续递增序列是 [2], 长度为1。

  提示：

  • 1 <= nums.length <= 104
  • -109 <= nums[i] <= 109

• 解法

  解法一：双指针

  不断地寻找连续递增子序列的长度，取最长。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public int findLengthOfLCIS(int[] nums) { if(nums.length<=1) return nums.length; int ans = 1; int tmp = 1; for(int l=0,r=1;l<nums.length&&r<nums.length;){ if(nums[r]>nums[l]){ l++;r++; tmp++; }else{ tmp = Math.max(tmp,ans); ans = tmp; tmp = 1; l = r; r++; } } // 额外检验递增序列 return tmp>ans?tmp:ans; } }

  解法二：贪心

  下面的算法其实和双指针本质上是一个东西。

  贪心

day126

714. 买卖股票的最佳时机含手续费

• 题目

  给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

  你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

  返回获得利润的最大值。

  **注意：**这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

  示例 1：

  1 2 3 4 5 6 7 8

  输入：prices = [1, 3, 2, 8, 4, 9], fee = 2 输出：8 解释：能够达到的最大利润: 在此处买入 prices[0] = 1 在此处卖出 prices[3] = 8 在此处买入 prices[4] = 4 在此处卖出 prices[5] = 9 总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8

  示例 2：

  1 2	输入：prices = [1,3,7,5,10,3], fee = 3 输出：6

  提示：

  • 1 <= prices.length <= 5 * 104
  • 1 <= prices[i] < 5 * 104
  • 0 <= fee < 5 * 104

• 解法

  解法一：dp

  本题只是在【188. 买卖股票的最佳时机 IV】的基础上再附加手续费。所以，我们直接在原来的动态规划转移方程上再加上“如果是买入股票，无需处理；如果是卖出股票，需增加手续费”。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

  class Solution { public int maxProfit(int[] prices, int fee) { // dp[i][j]表示第i天（从1开始），第j个状态的最大利润 int[][] dp = new int[prices.length+1][2*prices.length+1]; // 初始化 for(int i=0;i<2*prices.length+1;i++){ if(i%2==1) dp[0][i] = - prices[0]; } int s = 0; int fuhao = 0; for(int i=1;i<=prices.length;i++){ for(int j=0;j<2*prices.length;j++){ fuhao = (int)Math.pow(-1,j+1); if (fuhao==1 ){ s = fee; }else { s = 0; } dp[i][j+1] = Math.max(dp[i-1][j]+fuhao*prices[i-1] - s ,dp[i-1][j+1]); } } return dp[prices.length][2*prices.length]; } }

  上面的解法中，定义的状态太多，有较高的空间复杂度。leetcode提交中，显示“内存超出限制”。

  解法二：优化dp

  优化dp

day127

208. 实现 Trie (前缀树)

• 题目

  Trie（发音类似 “try”）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

  请你实现 Trie 类：

  • Trie() 初始化前缀树对象。
  • void insert(String word) 向前缀树中插入字符串 word 。
  • boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
  • boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

  示例：

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  输入 ["Trie", "insert", "search", "search", "startsWith", "insert", "search"] [[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]] 输出 [null, null, true, false, true, null, true] 解释 Trie trie = new Trie(); trie.insert("apple"); trie.search("apple"); // 返回 True trie.search("app"); // 返回 False trie.startsWith("app"); // 返回 True trie.insert("app"); trie.search("app"); // 返回 True

  提示：

  • 1 <= word.length, prefix.length <= 2000
  • word 和 prefix 仅由小写英文字母组成
  • insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次

• 解法

  解法一：模拟

  就是不断地去匹配寻找Trie树的下一个节点

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60

  class Trie { boolean isWord; // 单词是否以当前字符结尾 Trie[] nextNode; public Trie() { nextNode = new Trie[26]; } public void insert(String word) { Trie root = this; for(int i=0;i<word.length();i++){ int idx = word.charAt(i)-'a'; if(root.nextNode[idx]==null){ Trie n = new Trie(); root.nextNode[idx] = n; } root = root.nextNode[idx]; } root.isWord = true; return; } public boolean search(String word) { Trie root = this; for(int i=0;i<word.length();i++){ int idx = word.charAt(i)-'a'; if(root.nextNode[idx]==null){ return false; } root = root.nextNode[idx]; } return root.isWord; } public boolean startsWith(String prefix) { Trie root = this; for(int i=0;i<prefix.length();i++){ int idx = prefix.charAt(i)-'a'; if(root.nextNode[idx]==null){ return false; } root = root.nextNode[idx]; } return true; } } /** * Your Trie object will be instantiated and called as such: * Trie obj = new Trie(); * obj.insert(word); * boolean param_2 = obj.search(word); * boolean param_3 = obj.startsWith(prefix); */

day128

718. 最长重复子数组

• 题目

  给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

  示例 1：

  1 2 3

  输入：nums1 = [1,2,3,2,1], nums2 = [3,2,1,4,7] 输出：3 解释：长度最长的公共子数组是 [3,2,1] 。

  示例 2：

  1 2	输入：nums1 = [0,0,0,0,0], nums2 = [0,0,0,0,0] 输出：5

  提示：

  • 1 <= nums1.length, nums2.length <= 1000
  • 0 <= nums1[i], nums2[i] <= 100

• 代码

  解法一：暴力算法

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

  class Solution { public int findLength(int[] nums1, int[] nums2) { int maxLen = 0; for(int i=0;i<nums1.length;i++){ for(int j=0;j<nums2.length;j++){ int k=0; while(i+k<nums1.length&&j+k<nums2.length&&nums1[i+k]==nums2[j+k]){ k+=1; } if(maxLen<k) maxLen = k; } } return maxLen; } }

  解法二：动态规划

  思路及算法

  暴力解法的过程中，我们发现最坏情况下对于任意 i 与 j ，A[i] 与 B[j] 比较了 min⁡(i+1,j+1) 次。这也是导致了该暴力解法时间复杂度过高的根本原因。

  不妨设 A 数组为 [1, 2, 3]，B 两数组为为 [1, 2, 4] ，那么在暴力解法中 A[2] 与 B[2] 被比较了三次。这三次比较分别是我们计算 A[0:] 与 B[0:] 最长公共前缀、 A[1:] 与 B[1:] 最长公共前缀以及 A[2:] 与 B[2:] 最长公共前缀时产生的。

  我们希望优化这一过程，使得任意一对 A[i] 和 B[j] 都只被比较一次。这样我们自然而然想到利用这一次的比较结果。如果 A[i] == B[j]，那么我们知道 A[i:] 与 B[j:] 的最长公共前缀为 A[i + 1:] 与 B[j + 1:] 的最长公共前缀的长度加一，否则我们知道 A[i:] 与 B[j:] 的最长公共前缀为零。

  这样我们就可以提出动态规划的解法：令 dp[i][j] 表示 A[i:] 和 B[j:] 的最长公共前缀，那么答案即为所有 dp[i][j] 中的最大值。如果 A[i] == B[j]，那么 dp[i][j] = dp[i + 1][j + 1] + 1，否则 dp[i][j] = 0。

  这里借用了 Python 表示数组的方法，A[i:] 表示数组 A 中索引 i 到数组末尾的范围对应的子数组。

  考虑到这里 dp[i][j] 的值从 dp[i + 1][j + 1] 转移得到，所以我们需要倒过来，首先计算 dp[len(A) - 1][len(B) - 1]，最后计算 dp[0][0]。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public int findLength(int[] nums1, int[] nums2) { // dp[i][j]表示nums1[i:]和nums2[j:]的最长公共前缀长度 int[][] dp = new int[nums1.length+1][nums2.length+1]; int max =0; for(int i=nums1.length-1;i>=0;i--){ for(int j= nums2.length-1;j>=0;j--){ if(nums1[i]==nums2[j]){ dp[i][j] = dp[i+1][j+1]+1; } max = Math.max(dp[i][j],max); } } return max; } }

day129

1035. 不相交的线

• 题目

  在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

  现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

  • nums1[i] == nums2[j]
  • 且绘制的直线不与任何其他连线（非水平线）相交。

  请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

  以这种方法绘制线条，并返回可以绘制的最大连线数。

  示例 1：

  

  1 2 3 4

  输入：nums1 = [1,4,2], nums2 = [1,2,4] 输出：2 解释：可以画出两条不交叉的线，如上图所示。 但无法画出第三条不相交的直线，因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。

  示例 2：

  1 2	输入：nums1 = [2,5,1,2,5], nums2 = [10,5,2,1,5,2] 输出：3

  示例 3：

  1 2	输入：nums1 = [1,3,7,1,7,5], nums2 = [1,9,2,5,1] 输出：2

  提示：

  • 1 <= nums1.length, nums2.length <= 500
  • 1 <= nums1[i], nums2[j] <= 2000

• 解法

  解法一：动态规划

  其实这个问题本质上就是求解最长公共子序列问题

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  class Solution { public int maxUncrossedLines(int[] nums1, int[] nums2) { // dp[i][j]表示nums1[:i]与nums2[:j]中最长公共子序列的长度 int[][] dp = new int[nums1.length+1][nums2.length+1]; // 初始状态 dp[0][0] = 0; for(int i=1;i<=nums1.length;i++){ for(int j=1;j<=nums2.length;j++){ if(nums1[i-1]==nums2[j-1]){ dp[i][j] = dp[i-1][j-1]+1; }else{ dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]); } } } return dp[nums1.length][nums2.length]; } }

day130

1646. 获取生成数组中的最大值

• 题目

  给你一个整数 n 。按下述规则生成一个长度为 n + 1 的数组 nums ：

  • nums[0] = 0
  • nums[1] = 1
  • 当 2 <= 2 * i <= n 时，nums[2 * i] = nums[i]
  • 当 2 <= 2 * i + 1 <= n 时，nums[2 * i + 1] = nums[i] + nums[i + 1]

  返回生成数组 nums 中的 最大 值。

  示例 1：

  1 2 3 4 5 6 7 8 9 10 11 12

  输入：n = 7 输出：3 解释：根据规则： nums[0] = 0 nums[1] = 1 nums[(1 * 2) = 2] = nums[1] = 1 nums[(1 * 2) + 1 = 3] = nums[1] + nums[2] = 1 + 1 = 2 nums[(2 * 2) = 4] = nums[2] = 1 nums[(2 * 2) + 1 = 5] = nums[2] + nums[3] = 1 + 2 = 3 nums[(3 * 2) = 6] = nums[3] = 2 nums[(3 * 2) + 1 = 7] = nums[3] + nums[4] = 2 + 1 = 3 因此，nums = [0,1,1,2,1,3,2,3]，最大值 3

  示例 2：

  1 2 3

  输入：n = 2 输出：1 解释：根据规则，nums[0]、nums[1] 和 nums[2] 之中的最大值是 1

  示例 3：

  1 2 3

  输入：n = 3 输出：2 解释：根据规则，nums[0]、nums[1]、nums[2] 和 nums[3] 之中的最大值是 2

  提示：

  • 0 <= n <= 100

• 解法

  解法一：模拟

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  class Solution { public int getMaximumGenerated(int n) { if(n<=0) return 0; int max = 1; int[] nums = new int[n+1]; nums[1] = 1; for(int i=2;i<=n;i++){ if(i%2==0){ nums[i] = nums[i/2]; }else{ nums[i] = nums[(i-1)/2] + nums[(i+1)/2]; } max = Math.max(max,nums[i]); } // System.out.println(Arrays.toString(nums)); return max; } }

day131

79. 单词搜索

• 题目

• 解法

  解法一：二进制法和dfs法

  官方解法

  解法二：暴力dfs

  思路比较简单，对每一个位置进行四个方向的dfs，找到即可结束dfs了。

  结束条件：当前i处字符相等，且是word最后一个字符，可以return true了

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50

  class Solution { public boolean exist(char[][] board, String word) { boolean ok =false; boolean[][] v = new boolean[board.length][board[0].length]; for(int i=0;i<board.length;i++){ for(int j=0;j<board[0].length;j++){ ok = dfs(board,word,i,j,0,v); if(ok) return true; // System.out.println(ok); } } return false; } public boolean dfs(char[][] board,String word,int nextI,int nextJ,int i,boolean[][] v){ if(word.charAt(i)!=board[nextI][nextJ]){ return false; }else if (i == word.length() - 1) { return true; } // System.out.println(board[nextI][nextJ]); v[nextI][nextJ] = true; boolean ok = false; // 四个方向dfs if(ok_(board,nextI+1,nextJ)&&!v[nextI+1][nextJ]){// 右 ok = ok||dfs(board,word,nextI+1,nextJ,i+1,v); } if(ok_(board,nextI-1,nextJ)&&!v[nextI-1][nextJ]){// 左 ok = ok||dfs(board,word,nextI-1,nextJ,i+1,v); } if(ok_(board,nextI,nextJ+1)&&!v[nextI][nextJ+1]){// 下 ok = ok||dfs(board,word,nextI,nextJ+1,i+1,v); } if(ok_(board,nextI,nextJ-1)&&!v[nextI][nextJ-1]){// 上 ok = ok||dfs(board,word,nextI,nextJ-1,i+1,v); } v[nextI][nextJ] = false; return ok; } public boolean ok_(char[][] board,int newi,int newj){ return newi >= 0 && newi < board.length && newj >= 0 && newj < board[0].length; } }

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47

  func exist(board [][]byte, word string) bool { var dfs func(step,row,col int) v := make([][]bool,len(board)) m:=len(board) n:=len(board[0]) for i:=0;i<len(board);i++{ v[i]=make([]bool,len(board[0])) } check:=func(i,j int)bool{ return i>=0&&i<m&&j>=0&&j<n } ans:=false dfs = func(step,row,col int){ if board[row][col]!=word[step]{ return } if step==len(word)-1{ ans = true return } // fmt.Println(string(board[row][col]),string(word[step])) v[row][col]=true dir:=[][]int{{-1,0},{1,0},{0,1},{0,-1}} for i:=0;i<4;i++{ newrow:=row+dir[i][0] newcol:=col+dir[i][1] if check(newrow,newcol)&&!v[newrow][newcol]{ dfs(step+1,newrow,newcol) } } v[row][col]=false } for i:=0;i<m;i++{ for j:=0;j<n;j++{ if word[0]==board[i][j] { // 开始dfs dfs(0,i,j) if ans { return ans } } } } return false }

day132

36. 有效的数独

• 题目

  请你判断一个 9 x 9 的数独是否有效。只需要 根据以下规则 ，验证已经填入的数字是否有效即可。

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

  注意：

  • 一个有效的数独（部分已被填充）不一定是可解的。
  • 只需要根据以上规则，验证已经填入的数字是否有效即可。
  • 空白格用 '.' 表示。

  示例 1：

  

  1 2 3 4 5 6 7 8 9 10 11

  输入：board = [["5","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出：true

  示例 2：

  1 2 3 4 5 6 7 8 9 10 11 12

  输入：board = [["8","3",".",".","7",".",".",".","."] ,["6",".",".","1","9","5",".",".","."] ,[".","9","8",".",".",".",".","6","."] ,["8",".",".",".","6",".",".",".","3"] ,["4",".",".","8",".","3",".",".","1"] ,["7",".",".",".","2",".",".",".","6"] ,[".","6",".",".",".",".","2","8","."] ,[".",".",".","4","1","9",".",".","5"] ,[".",".",".",".","8",".",".","7","9"]] 输出：false 解释：除了第一行的第一个数字从 5 改为 8 以外，空格内其他数字均与 示例1 相同。 但由于位于左上角的 3x3 宫内有两个 8 存在, 因此这个数独是无效的。

  提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j] 是一位数字（1-9）或者 '.'

• 解法

  数组哈希法

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  class Solution { public boolean isValidSudoku(char[][] board) { int[][] rows = new int[9][9]; int[][] columns = new int[9][9]; int[][][] subboxes = new int[3][3][9]; for (int i = 0; i < 9; i++) { for (int j = 0; j < 9; j++) { char c = board[i][j]; if (c != '.') { int index = c - '0' - 1; rows[i][index]++; columns[j][index]++; subboxes[i / 3][j / 3][index]++; if (rows[i][index] > 1 || columns[j][index] > 1 || subboxes[i / 3][j / 3][index] > 1) { return false; } } } } return true; } }

day133

37. 解数独

• 题目

  编写一个程序，通过填充空格来解决数独问题。

  数独的解法需 遵循如下规则：

  1. 数字 1-9 在每一行只能出现一次。
  2. 数字 1-9 在每一列只能出现一次。
  3. 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图）

  数独部分空格内已填入了数字，空白格用 '.' 表示。

  示例 1：

  

  1 2 3

  输入：board = [["5","3",".",".","7",".",".",".","."],["6",".",".","1","9","5",".",".","."],[".","9","8",".",".",".",".","6","."],["8",".",".",".","6",".",".",".","3"],["4",".",".","8",".","3",".",".","1"],["7",".",".",".","2",".",".",".","6"],[".","6",".",".",".",".","2","8","."],[".",".",".","4","1","9",".",".","5"],[".",".",".",".","8",".",".","7","9"]] 输出：[["5","3","4","6","7","8","9","1","2"],["6","7","2","1","9","5","3","4","8"],["1","9","8","3","4","2","5","6","7"],["8","5","9","7","6","1","4","2","3"],["4","2","6","8","5","3","7","9","1"],["7","1","3","9","2","4","8","5","6"],["9","6","1","5","3","7","2","8","4"],["2","8","7","4","1","9","6","3","5"],["3","4","5","2","8","6","1","7","9"]] 解释：输入的数独如上图所示，唯一有效的解决方案如下所示：

  提示：

  • board.length == 9
  • board[i].length == 9
  • board[i][j] 是一位数字或者 '.'
  • 题目数据 保证 输入数独仅有一个解

• 解法

  解法一：dfs+回溯

  其实题目的解法很明显，dfs暴搜，主要是回溯的过程和以往的题目不太一样：填数独并不是挨着格子填的，所以回溯的时候也不是挨着格子回溯，先记录这些空格子的位置，回溯的时候按照记录来回溯即可

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40

  class Solution { private boolean[][] line = new boolean[9][9]; private boolean[][] column = new boolean[9][9]; private boolean[][][] block = new boolean[3][3][9]; private boolean valid = false; private List<int[]> spaces = new ArrayList<int[]>(); public void solveSudoku(char[][] board) { for (int i = 0; i < 9; ++i) { for (int j = 0; j < 9; ++j) { if (board[i][j] == '.') { spaces.add(new int[]{i, j}); } else { int digit = board[i][j] - '0' - 1; line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true; } } } dfs(board, 0); } public void dfs(char[][] board, int pos) { if (pos == spaces.size()) { valid = true; return; } int[] space = spaces.get(pos); int i = space[0], j = space[1]; for (int digit = 0; digit < 9 && !valid; ++digit) { if (!line[i][digit] && !column[j][digit] && !block[i / 3][j / 3][digit]) { line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = true; board[i][j] = (char) (digit + '0' + 1); dfs(board, pos + 1); line[i][digit] = column[j][digit] = block[i / 3][j / 3][digit] = false; } } } }

  其他解法

  https://leetcode.cn/problems/sudoku-solver/solutions/414120/jie-shu-du-by-leetcode-solution/

day134

51. N 皇后

• 题目

  按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

  n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

  给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

  每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

  示例 1：

  

  1 2 3

  输入：n = 4 输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]] 解释：如上图所示，4 皇后问题存在两个不同的解法。

  示例 2：

  1 2	输入：n = 1 输出：[["Q"]]

  提示：

  • 1 <= n <= 9

• 解法

  解法一：dfs+回溯

  https://leetcode.cn/problems/n-queens/solutions/398929/nhuang-hou-by-leetcode-solution/

day135

52. N 皇后 II

• 题目

  n 皇后问题 研究的是如何将 n 个皇后放置在 n × n 的棋盘上，并且使皇后彼此之间不能相互攻击。

  给你一个整数 n ，返回 n 皇后问题 不同的解决方案的数量。

  示例 1：

  

  1 2 3

  输入：n = 4 输出：2 解释：如上图所示，4 皇后问题存在两个不同的解法。

  示例 2：

  1 2	输入：n = 1 输出：1

  提示：

  • 1 <= n <= 9

• 解法

  解法一：dfs+回溯

  https://leetcode.cn/problems/n-queens-ii/solutions/449388/nhuang-hou-ii-by-leetcode-solution/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34

  class Solution { int total = 0; public int totalNQueens(int n) { int[] queens = new int[n]; Arrays.fill(queens,-1); Set<Integer> column = new HashSet<>(); Set<Integer> l = new HashSet<>(); Set<Integer> r = new HashSet<>(); dfs(n,0,column,l,r); return total; } public void dfs(int n,int k,Set<Integer> column,Set<Integer> l,Set<Integer> r){ if(k==n){ total++; return; } for(int i=0;i<n;i++){ if(column.contains(i)) continue; if(l.contains(k-i)) continue; if(r.contains(k+i)) continue; column.add(i); l.add(k-i); r.add(k+i); dfs(n,k+1,column,l,r); column.remove(i); l.remove(k-i); r.remove(k+i); } } }

day136

191. 位1的个数

• 题目

  编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

  提示：

  • 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
  • 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在 示例 3 中，输入表示有符号整数 -3。

  示例 1：

  1 2 3

  输入：n = 00000000000000000000000000001011 输出：3 解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 '1'。

  示例 2：

  1 2 3

  输入：n = 00000000000000000000000010000000 输出：1 解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 '1'。

  示例 3：

  1 2 3

  输入：n = 11111111111111111111111111111101 输出：31 解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 '1'。

  提示：

  • 输入必须是长度为 32 的 二进制串 。

  进阶：

  • 如果多次调用这个函数，你将如何优化你的算法？

• 解法

  解法一：位运算

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  public class Solution { // you need to treat n as an unsigned value public int hammingWeight(int n) { int cnt = 0; while(n!=0){ if(n<0) { // 取最高位 if(((n>>31)&1)==1) cnt++; n<<=1; }else { // 取最低位 if((n&1)==1) cnt++; n>>=1; } } return cnt; } }

day137

231. 2 的幂

• 题目

  给你一个整数 n，请你判断该整数是否是 2 的幂次方。如果是，返回 true ；否则，返回 false 。

  如果存在一个整数 x 使得 n == 2x ，则认为 n 是 2 的幂次方。

  示例 1：

  1 2 3

  输入：n = 1 输出：true 解释：20 = 1

  示例 2：

  1 2 3

  输入：n = 16 输出：true 解释：24 = 16

  示例 3：

  1 2	输入：n = 3 输出：false

  示例 4：

  1 2	输入：n = 4 输出：true

  示例 5：

  1 2	输入：n = 5 输出：false

  提示：

  • -231 <= n <= 231 - 1

  **进阶：**你能够不使用循环/递归解决此问题吗？

• 解法

  解法一：位运算

  32个bit位，最多只有一个bit位为1才是2的幂，否则不是。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  class Solution { public boolean isPowerOfTwo(int n) { boolean ok =false; if(n<=0) return false; int cnt =0; for(int i=0;i<32;i++){ if((n&(1<<i))!=0) { cnt++; if(cnt>1) return false; } } return true; } }

  进阶：O(1)实现

  https://leetcode.cn/problems/power-of-two/solutions/796201/2de-mi-by-leetcode-solution-rny3/

  1 2 3 4 5 6 7 8 9 10 11 12 13

  // n & (n - 1)移除最低位的1，这样还剩1的话，说明不满足 class Solution { public boolean isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; } } // n & -n 直接获取最低位1. 并且n>0，n & -n = n。所以n为2的幂 class Solution { public boolean isPowerOfTwo(int n) { return n > 0 && (n & -n) == n; } }

day138

200. 岛屿数量

• 题目

• 解法

  解法一：并查集

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70

  class Solution { public int numIslands(char[][] grid) { int m = grid.length,n = grid[0].length; int x = 0; for(int i=0;i<m;i++){ for(int j=0;j<n;j++){ if(grid[i][j]=='0') x++; } } Uf uf = new Uf(n*m); for(int i=0;i<m;i++){ for(int j=0;j<n;j++){ if(grid[i][j]=='1') { needUf(grid,i,j,m,n,uf); } } } return uf.count - x; } // 判断当前网格是否需要union. 是岛屿且与前面的连通 public void needUf(char[][] grid,int i,int j,int row,int col,Uf uf){ int[][] dirs = new int[][]{{0,-1},{0,1},{1,0},{-1,0}}; for(int[] dir:dirs){ int newi = i+dir[0],newj = j+dir[1]; if(newi<0||newi>=row||newj<0||newj>=col) continue; if(grid[newi][newj] == '1') { if(!uf.connected(newi*col+newj,i*col+j)){ uf.union(newi*col+newj,i*col+j); } } } return; } } class Uf{ int count; // 连通分量 int[] parents; // 存储每个节点的父节点 public Uf(int n){ count = n; parents = new int[n]; for(int i=0;i<n;i++){ parents[i] = i; } } // 将两个点连通 public void union(int p,int q){ int rootp = find(p); int rootq = find(q); if(rootp==rootq) return; parents[rootp] = rootq; count--; } public boolean connected(int p,int q){ return find(p)==find(q); } // 查找x的根节点 public int find(int x){ if(x!=parents[x]){ x = find(parents[x]); } return parents[x]; } }

day139

547. 省份数量

• 题目

  有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

  省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

  给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。

  返回矩阵中 省份 的数量。

  示例 1：

  

  1 2	输入：isConnected = [[1,1,0],[1,1,0],[0,0,1]] 输出：2

  示例 2：

  

  1 2	输入：isConnected = [[1,0,0],[0,1,0],[0,0,1]] 输出：3

  提示：

  • 1 <= n <= 200
  • n == isConnected.length
  • n == isConnected[i].length
  • isConnected[i][j] 为 1 或 0
  • isConnected[i][i] == 1
  • isConnected[i][j] == isConnected[j][i]

• 解法

  解法一：并查集

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49

  class Solution { public int findCircleNum(int[][] isConnected) { int n=isConnected.length; UF uf = new UF(n); for(int i=0;i<n;i++){ for(int j=i+1;j<n;j++){ // 剪枝：对称矩阵只需要对角线一半即可 if(isConnected[i][j]==1/*&&!uf.connected(i,j)*/){ uf.union(i,j); } } } return uf.cnt; } } class UF{ int cnt; // 连通分量个数 int[] parents; // 存储父节点 public UF(int n){ cnt = n; parents = new int[n]; for(int i=0;i<n;i++) parents[i] = i; } public void union(int a,int b){ int ra = find(a); int rb = find(b); if(ra==rb) return; // 已经连通 parents[ra] = rb; // 没连通，就将其中一个根节点拼上去 // parents[rb] = ra; cnt--; } // 判断a和b是否连通（是否含有相同根节点） public boolean connected(int a, int b){ return find(a)==find(b); } // 寻找根节点 public int find(int x){ if(x!=parents[x]){ parents[x] = find(parents[x]); } return parents[x]; } }

day140

2. 两数相加

• 题目

  给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

  请你将两个数相加，并以相同形式返回一个表示和的链表。

  你可以假设除了数字 0 之外，这两个数都不会以 0 开头。

  示例 1：

  

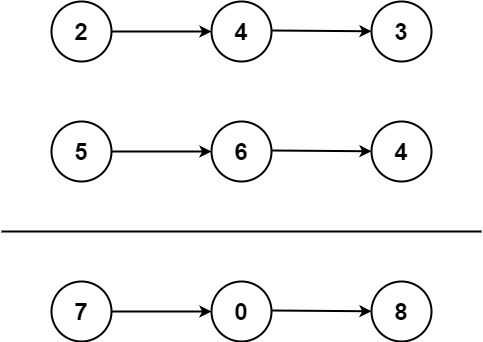
  1 2 3

  输入：l1 = [2,4,3], l2 = [5,6,4] 输出：[7,0,8] 解释：342 + 465 = 807.

  示例 2：

  1 2	输入：l1 = [0], l2 = [0] 输出：[0]

  示例 3：

  1 2	输入：l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9] 输出：[8,9,9,9,0,0,0,1]

  提示：

  • 每个链表中的节点数在范围 [1, 100] 内
  • 0 <= Node.val <= 9
  • 题目数据保证列表表示的数字不含前导零

• 解法

  解法一：模拟

  模拟数学上两数相加法则：低位相加大于10，减10得进位1，模10得本位。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53

  /** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func addTwoNumbers(l1 *ListNode, l2 *ListNode) *ListNode { jw := 0 l3 := &ListNode{} tmp := l3 rs := 0 for l1!=nil&&l2!=nil { rs = l1.Val+l2.Val+jw; tmp.Val = rs%10 jw = rs/10 if(l1.Next!=nil||l2.Next!=nil){ tmp.Next = new(ListNode) tmp = tmp.Next } l1 = l1.Next l2 = l2.Next } for(l1!=nil){ rs = l1.Val+jw tmp.Val = rs%10 jw = rs/10 if(l1.Next!=nil){ tmp.Next = new(ListNode) tmp = tmp.Next } l1=l1.Next } for(l2!=nil){ rs = l2.Val+jw tmp.Val = rs%10 jw = rs/10 if(l2.Next!=nil) { tmp.Next = new(ListNode) tmp = tmp.Next } l2=l2.Next } if(jw!=0){ tmp.Next = new(ListNode) tmp.Next.Val = jw } return l3 }

day141

3. 无重复字符的最长子串

• 题目

  给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

  示例 1:

  1 2 3

  输入: s = "abcabcbb" 输出: 3 解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

  示例 2:

  1 2 3

  输入: s = "bbbbb" 输出: 1 解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

  示例 3:

  1 2 3 4

  输入: s = "pwwkew" 输出: 3 解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。 请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

  提示：

  • 0 <= s.length <= 5 * 104
  • s 由英文字母、数字、符号和空格组成

• 解法

  解法一：滑动窗口

  https://leetcode.cn/problems/longest-substring-without-repeating-characters/solutions/227999/wu-zhong-fu-zi-fu-de-zui-chang-zi-chuan-by-leetc-2/

day142

4. 寻找两个正序数组的中位数

• 题目

  给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

  算法的时间复杂度应该为 O(log (m+n)) 。

  示例 1：

  1 2 3

  输入：nums1 = [1,3], nums2 = [2] 输出：2.00000 解释：合并数组 = [1,2,3] ，中位数 2

  示例 2：

  1 2 3

  输入：nums1 = [1,2], nums2 = [3,4] 输出：2.50000 解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

  提示：

  • nums1.length == m
  • nums2.length == n
  • 0 <= m <= 1000
  • 0 <= n <= 1000
  • 1 <= m + n <= 2000
  • -106 <= nums1[i], nums2[i] <= 106

• 解法

  解法一：双指针

  这个问题最核心的就是合并两个有序数组。我们使用双指针算法：一个指针指向数组nums1首部，另一个指向数组nums2首部，然后比较大小，最小的放到新数组最前面，然后移动那个最小指针再和其他数组指针比较。如果某个数组元素提前结束，将这个数组的后面元素附加过来

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28

  func findMedianSortedArrays(nums1 []int, nums2 []int) float64 { // 合并 nums := make([]int,len(nums1)+len(nums2)) i1:=0 i2:=0 for i:=0;i<len(nums);i++ { if i1<len(nums1)&&i2<len(nums2) { if nums1[i1]<nums2[i2]{ nums[i] = nums1[i1] i1++ }else{ nums[i] = nums2[i2] i2++ } }else if i1>=len(nums1) && i2 <len(nums2) { nums[i] = nums2[i2] i2++ }else if i1<len(nums1) && i2 >=len(nums2){ nums[i] = nums1[i1] i1++ } } if len(nums)%2==1{ return float64(nums[len(nums)/2]) } return (0.0 + float64(nums[len(nums)/2]+nums[len(nums)/2-1])) / 2 }

day143

5. 最长回文子串

• 题目

  给你一个字符串 s，找到 s 中最长的回文子串。

  如果字符串的反序与原始字符串相同，则该字符串称为回文字符串。

  示例 1：

  1 2 3

  输入：s = "babad" 输出："bab" 解释："aba" 同样是符合题意的答案。

  示例 2：

  1 2	输入：s = "cbbd" 输出："bb"

  提示：

  • 1 <= s.length <= 1000
  • s 仅由数字和英文字母组成

• 解法

  解法一：动态规划

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  func longestPalindrome(s string) string { len:=len(s) if len<2 { return s } maxlen:=1 begin:=0 dp := make([][]bool, len) // 初始化：长度为1的是回文串；长度为2的子串，但是两个字符相等的也是子串 for i := 0; i < len; i++ { dp[i] = make([]bool, len) dp[i][i] = true if i<len-1&&s[i]==s[i+1]{ dp[i][i+1] = true } } // 状态转移：P(i,j)=P(i+1,j−1)∧(Si==Sj) for L:=2;L<=len;L++{ for i:=0;i<len;i++{ j:=i+L-1 if j>=len { break } if s[i] == s[j] && j-i+1>2 { dp[i][j] = dp[i+1][j-1] } if dp[i][j] && maxlen<j-i+1{ maxlen = j-i+1 begin = i } } } return s[begin:begin+maxlen] }

day144

10. 正则表达式匹配

• 题目

  给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。

  • '.' 匹配任意单个字符
  • '*' 匹配零个或多个前面的那一个元素

  所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

  示例 1：

  1 2 3

  输入：s = "aa", p = "a" 输出：false 解释："a" 无法匹配 "aa" 整个字符串。

  示例 2:

  1 2 3

  输入：s = "aa", p = "a*" 输出：true 解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

  示例 3：

  1 2 3

  输入：s = "ab", p = ".*" 输出：true 解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

  提示：

  • 1 <= s.length <= 20
  • 1 <= p.length <= 20
  • s 只包含从 a-z 的小写字母。
  • p 只包含从 a-z 的小写字母，以及字符 . 和 *。
  • 保证每次出现字符 * 时，前面都匹配到有效的字符

• 解法

  解法一：动态规划

  https://leetcode.cn/problems/regular-expression-matching/solutions/296114/shou-hui-tu-jie-wo-tai-nan-liao-by-hyj8/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38

  func isMatch(s string, p string) bool { m, n := len(s), len(p) // if m==0||n==0 {return false} // dp[i][j]表示s[:i]是否与p[:j]匹配 dp := make([][]bool, m+1) for i:=0;i<=m;i++{ dp[i] = make([]bool,n+1) } matched := func(i,j int) bool { return s[i]==p[j]||p[j]=='.' } dp[0][0] = true for j:=1;j<=n;j++{ if p[j-1]=='*' { dp[0][j] = dp[0][j-2] } } for i:=1;i<m+1;i++{ for j:=1;j<n+1;j++{ if matched(i-1,j-1){ dp[i][j] = dp[i-1][j-1] }else{ if p[j-1]=='*'{ if matched(i-1,j-2){// 三种情况 dp[i][j] = dp[i-1][j-1]||dp[i][j-2]||dp[i-1][j] }else{ dp[i][j] = dp[i][j-2] } } } } } return dp[m][n] }

day145

21. 合并两个有序链表

• 题目

  将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

  示例 1：

  

  1 2	输入：l1 = [1,2,4], l2 = [1,3,4] 输出：[1,1,2,3,4,4]

  示例 2：

  1 2	输入：l1 = [], l2 = [] 输出：[]

  示例 3：

  1 2	输入：l1 = [], l2 = [0] 输出：[0]

  提示：

  • 两个链表的节点数目范围是 [0, 50]
  • -100 <= Node.val <= 100
  • l1 和 l2 均按 非递减顺序 排列

• 解法

  解法一：双指针

  两个指针分别指向两个链表首部，依次比较首部大小，将小的从所在链表移除并移入到新的链表中，如果某个链表为空，则将另一个非空链表直接拿过来

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  /** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func mergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode { dummpy:=&ListNode{} tmp:=dummpy for list1!=nil||list2!=nil { if list1!=nil&&list2!=nil{ if list1.Val>list2.Val { tmp.Next = list2 tmp = tmp.Next list2 = list2.Next }else{ tmp.Next = list1 tmp = tmp.Next list1 = list1.Next } }else if list1==nil&&list2!=nil { tmp.Next = list2 list2 = nil }else if list1!=nil&&list2==nil{ tmp.Next = list1 list1 = nil } } return dummpy.Next }

day146

23. 合并 K 个升序链表

• 题目

  给你一个链表数组，每个链表都已经按升序排列。

  请你将所有链表合并到一个升序链表中，返回合并后的链表。

  示例 1：

  1 2 3 4 5 6 7 8 9 10

  输入：lists = [[1,4,5],[1,3,4],[2,6]] 输出：[1,1,2,3,4,4,5,6] 解释：链表数组如下： [ 1->4->5, 1->3->4, 2->6 ] 将它们合并到一个有序链表中得到。 1->1->2->3->4->4->5->6

  示例 2：

  1 2	输入：lists = [] 输出：[]

  示例 3：

  1 2	输入：lists = [[]] 输出：[]

  提示：

  • k == lists.length
  • 0 <= k <= 10^4
  • 0 <= lists[i].length <= 500
  • -10^4 <= lists[i][j] <= 10^4
  • lists[i] 按 升序 排列
  • lists[i].length 的总和不超过 10^4

• 解法

  解法一：顺序地两两合并

  k个链表合并可以抽象出两个链表进行合并后再和第三个链表进行两两合并，如此往复

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48

  /** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func mergeKLists(lists []*ListNode) *ListNode { if len(lists)==0{ return nil }else if len(lists)==1{ return lists[0] } var tmp *ListNode for i:=0;i<len(lists);i++ { tmp = mergeTwoList(tmp,lists[i]) } return tmp } func mergeTwoList(l1,l2 *ListNode) *ListNode{ l:=&ListNode{} head :=l for l1!=nil&&l2!=nil{ if l1.Val<l2.Val{ l.Next = l1 l1 = l1.Next }else{ l.Next = l2 l2 = l2.Next } l = l.Next } for l1!=nil { l.Next = l1 l1 = nil } for l2!=nil{ l.Next = l2 l2 = nil } return head.Next }

  解法二：分治法

  不断将多个链表分成单个，然后两两配对合并

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52

  /** * Definition for singly-linked list. * type ListNode struct { * Val int * Next *ListNode * } */ func mergeKLists(lists []*ListNode) *ListNode { return split(lists,0,len(lists)-1) } func split(lists []*ListNode,l,r int) *ListNode { if l==r{ return lists[l] } if l>r{ return nil } mid :=(l+r)/2 l1:= split(lists,l,mid) l2:= split(lists,mid+1,r) return mergeTwoList(l1,l2) } func mergeTwoList(l1,l2 *ListNode) *ListNode{ l:=&ListNode{} head :=l for l1!=nil&&l2!=nil{ if l1.Val<l2.Val{ l.Next = l1 l1 = l1.Next }else{ l.Next = l2 l2 = l2.Next } l = l.Next } for l1!=nil { l.Next = l1 l1 = nil } for l2!=nil{ l.Next = l2 l2 = nil } return head.Next }

day147

31. 下一个排列

• 题目

  整数数组的一个 排列 就是将其所有成员以序列或线性顺序排列。

  • 例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

  整数数组的 下一个排列 是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的 下一个排列 就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

  • 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
  • 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。
  • 而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

  给你一个整数数组 nums ，找出 nums 的下一个排列。

  必须** 原地 **修改，只允许使用额外常数空间。

  示例 1：

  1 2	输入：nums = [1,2,3] 输出：[1,3,2]

  示例 2：

  1 2	输入：nums = [3,2,1] 输出：[1,2,3]

  示例 3：

  1 2	输入：nums = [1,1,5] 输出：[1,5,1]

  提示：

  • 1 <= nums.length <= 100
  • 0 <= nums[i] <= 100

• 解法

  解法一：找数学规律

  推导过程：

  1 2 3 4 5 6 7 8

  1,2,3->1,3,2 1,3,2->2,1,3 1,4,3,2->2,1,3,4 2,6,5,4,3,1->3,6,5,4,2,1->3,1,2,4,5,6-> 2,6,7,5,4,1->2,7,1,4,5,6 3,7,5,4,1->4,7,5,3,1->4,1,3,7,5 6,5,4,1->1,4,5,6 1,3,2,4,5,6,9,10,11,15,14,19,16->1,3,2,4,5,6,9,10,11,15,16,14,19

  从右往左看，碰到降序序列(两个就够了)，说明不需要修改降序序列前的顺序，只需要调整降序序列后，需要从后面的序列里挑出第一个大于当前降序序列首部的数字或没有也可以，然后再把后面的升序列反转。

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32

  func nextPermutation(nums []int) { if len(nums) <= 1 { return } i := len(nums) - 2 j := len(nums) - 1 k := len(nums) - 1 // 找降序序列（从右往左） for i >= 0 && j >= 0 { if nums[i] < nums[j] { break } i-- j-- } // i及其以后的序列是升序，i和j是降序（从右往左看） if i >= 0 { // 不是最后一个排列 // find: A[i]<A[k] for nums[i] >= nums[k] { k-- } // swap A[i], A[k] nums[i], nums[k] = nums[k], nums[i] } // 反转 for i,j:=j,len(nums)-1;i<j;i,j=i+1,j-1{ nums[i], nums[j] = nums[j], nums[i] } return }

day148

32. 最长有效括号

• 题目

  给你一个只包含 '(' 和 ')' 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

  示例 1：

  1 2 3

  输入：s = "(()" 输出：2 解释：最长有效括号子串是 "()"

  示例 2：

  1 2 3

  输入：s = ")()())" 输出：4 解释：最长有效括号子串是 "()()"

  示例 3：

  1 2	输入：s = "" 输出：0

  提示：

  • 0 <= s.length <= 3 * 104
  • s[i] 为 '(' 或 ')'

• 解法

  方法一：栈

  这个与普通括号匹配有点不一样，求解子串长度，因此我们只需要在栈中存放下标即可。为了分开不同连续子串括号，我们需要预留)作为分界线。

  https://leetcode.cn/problems/longest-valid-parentheses/solutions/314827/shou-hua-tu-jie-zhan-de-xiang-xi-si-lu-by-hyj8/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

  func longestValidParentheses(s string) int { stack := []int{-1} max:=0 for i:=0;i<len(s);i++{ if s[i]=='( stack = append(stack,i) }else{ stack = stack[:len(stack)-1] if len(stack)==0 { stack = append(stack,i) }else { l := i-stack[len(stack)-1] if l>max{ max = l } } } } return max }

  方法二：动态规划

  https://leetcode.cn/problems/longest-valid-parentheses/solutions/314683/zui-chang-you-xiao-gua-hao-by-leetcode-solution/

day149

42. 接雨水

• 题目

  给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

  示例 1：

  

  1 2 3

  输入：height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出：6 解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

  示例 2：

  1 2	输入：height = [4,2,0,3,2,5] 输出：9

  提示：

  • n == height.length
  • 1 <= n <= 2 * 104
  • 0 <= height[i] <= 105

• 解法

  官方三解法

  https://leetcode.cn/problems/trapping-rain-water/solutions/692342/jie-yu-shui-by-leetcode-solution-tuvc/

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37

  func trap(height []int) int { n:=len(height) ans:=0 if n<=1 { return ans } leftdp := make([]int,n) rightdp := make([]int,n) max := func(a,b int) int{ if a>b{ return a } return b } min := func(a,b int) int{ if a<b{ return a } return b } // 初始化 leftdp[0] = height[0] rightdp[n-1] = height[n-1] // 记录状态 for i:=1;i<n;i++{ leftdp[i] = max(leftdp[i-1],height[i]) } for i:=n-2;i>=0;i--{ rightdp[i] = max(rightdp[i+1],height[i]) } // 状态转移 for i:=0;i<n;i++{ ans += min(leftdp[i],rightdp[i]) - height[i] } return ans }

day150

48. 旋转图像

• 题目

• 解法

  解法一：找数学规律

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

  func rotate(matrix [][]int) { reverseColFunc := func(matrix [][]int,j int){ n:=len(matrix) for i:=0;i<n/2;i++{ matrix[i][j],matrix[n-i-1][j] = matrix[n-i-1][j],matrix[i][j] } } for j:=0;j<len(matrix[0]);j++{ reverseColFunc(matrix,j) } n:=len(matrix) m:=len(matrix[0]) for i:=0;i<n;i++{ for j:=i+1;j<m;j++{ matrix[i][j],matrix[j][i] = matrix[j][i],matrix[i][j] } } return } // 先按照列，对每一个列都进行反转 // 再进行矩阵对称变换

  反转还可以优化

  反转只需要O(n)

  1 2 3 4 5 6 7 8 9 10 11 12 13

  func rotate(matrix [][]int) { n := len(matrix) // 水平翻转 for i := 0; i < n/2; i++ { matrix[i], matrix[n-1-i] = matrix[n-1-i], matrix[i] } // 主对角线翻转 for i := 0; i < n; i++ { for j := 0; j < i; j++ { matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j] } } }

  其他解法

  https://leetcode.cn/problems/rotate-image/solutions/526980/xuan-zhuan-tu-xiang-by-leetcode-solution-vu3m/

day151

49. 字母异位词分组

• 题目

  给你一个字符串数组，请你将 字母异位词 组合在一起。可以按任意顺序返回结果列表。

  字母异位词 是由重新排列源单词的所有字母得到的一个新单词。

  示例 1:

  1 2	输入: strs = ["eat", "tea", "tan", "ate", "nat", "bat"] 输出: [["bat"],["nat","tan"],["ate","eat","tea"]]

  示例 2:

  1 2	输入: strs = [""] 输出: [[""]]

  示例 3:

  1 2	输入: strs = ["a"] 输出: [["a"]]

  提示：

  • 1 <= strs.length <= 104
  • 0 <= strs[i].length <= 100
  • strs[i] 仅包含小写字母

• 解法

  解法一：排序

  题目的核心在于如何判断两个字母是“字母异位词”？其实“字母异位词”排序后是相同字母，因此，我们可以借用哈希表来存储并去重：将排序后具有相同字符串的序列合并在一起即可

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  func groupAnagrams(strs []string) [][]string { ans := [][]string{} m := make(map[string][]string,0) for i:=0;i<len(strs);i++{ b:=[]byte(strs[i]) sort.Slice(b, func(i, j int) bool { return b[i] < b[j] }) key:=string(b) m[key] = append(m[key],strs[i]) } for _,v:=range m{ ans = append(ans,v) } return ans }

  解法二：计数

  https://leetcode.cn/problems/group-anagrams/solutions/520469/zi-mu-yi-wei-ci-fen-zu-by-leetcode-solut-gyoc/

day152

53. 最大子数组和

• 题目

  给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

  子数组 是数组中的一个连续部分。

  示例 1：

  1 2 3

  输入：nums = [-2,1,-3,4,-1,2,1,-5,4] 输出：6 解释：连续子数组 [4,-1,2,1] 的和最大，为 6 。

  示例 2：

  1 2	输入：nums = [1] 输出：1

  示例 3：

  1 2	输入：nums = [5,4,-1,7,8] 输出：23

  提示：

  • 1 <= nums.length <= 105
  • -104 <= nums[i] <= 104

  **进阶：**如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的 分治法 求解。

• 解法

  官方解法

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

  func maxSubArray(nums []int) int { dp := make([]int,len(nums)) max := func(a,b int) int{ if a>b { return a } return b } dp[0] = nums[0] ans := nums[0] for i:=1;i<len(nums);i++{ dp[i] = max(dp[i-1]+nums[i],nums[i]) ans = max(dp[i],ans) } return ans } // dp[i]表示第i个数结尾的连续子数组的最大和 // dp[i] = max(nums[i],dp[i-1]+nums[i]) // 第i个数可以加入连续子序列，也可以不加入连续子序列，新开始一个新的子序列，主要依据是看谁最大 // 然后，找出所有连续子数组的最大和

day153

75. 颜色分类

• 题目

• 解法

  解法一：排序

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31

  func sortColors(nums []int){ // 快速排序 // 分区 partition:=func(nums []int,start,end int)int{ pivot:=nums[end] left:=start right:=end for left<right{ for left<right&&nums[left]<=pivot{ left++ } for left<right&&nums[right]>=pivot{ right-- } // 交换 nums[left],nums[right] = nums[right],nums[left] } nums[left],nums[end] = nums[end],nums[left] return left } var qsort func(nums []int,left ,right int) qsort=func(nums []int,left,right int){ if left>=right{ return } p:=partition(nums,left,right) qsort(nums,left,p-1) qsort(nums,p+1,right) } qsort(nums,0,len(nums)-1) }

  解法二：单指针

  1 2 3 4 5 6 7 8 9 10 11 12 13 14

  func swapColors(colors []int, target int) (countTarget int) { for i, c := range colors { if c == target { colors[i], colors[countTarget] = colors[countTarget], colors[i] countTarget++ } } return } func sortColors(nums []int) { count0 := swapColors(nums, 0) // 把 0 排到前面 swapColors(nums[count0:], 1) // nums[:count0] 全部是 0 了，对剩下的 nums[count0:] 把 1 排到前面 }

  解法三：双指针

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18

  func sortColors(nums []int){ // 双指针 n0:=0 n1:=0 num:=0 for i:=0;i<len(nums);i++{ num=nums[i] nums[i]=2 if num<2{ nums[n1]=1 n1++ } if num<1{ nums[n0]=0 n0++ } } }

day154

76. 最小覆盖子串

• 题目

  给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

  注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。

  示例 1：

  1 2 3

  输入：s = "ADOBECODEBANC", t = "ABC" 输出："BANC" 解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

  示例 2：

  1 2 3

  输入：s = "a", t = "a" 输出："a" 解释：整个字符串 s 是最小覆盖子串。

  示例 3:

  1 2 3 4

  输入: s = "a", t = "aa" 输出: "" 解释: t 中两个字符 'a' 均应包含在 s 的子串中， 因此没有符合条件的子字符串，返回空字符串。

  提示：

  • m == s.length
  • n == t.length
  • 1 <= m, n <= 105
  • s 和 t 由英文字母组成

  **进阶：**你能设计一个在 o(m+n) 时间内解决此问题的算法吗？

• 解法

  解法一：滑动窗口+哈希表

  1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

  func minWindow(s string, t string) string { ori, cnt := map[byte]int{}, map[byte]int{} for i := 0; i < len(t); i++ { ori[t[i]]++ } sLen := len(s) len := math.MaxInt32 ansL, ansR := -1, -1 check := func() bool { for k, v := range ori { if cnt[k] < v { return false } } return true } for l, r := 0, 0; r < sLen; r++ { if r < sLen && ori[s[r]] > 0 { cnt[s[r]]++ } // 查看窗口是否覆盖t，若覆盖再移动左指针缩小窗口，否则继续移动右指针扩大窗口 for check() && l <= r { if (r - l + 1 < len) { len = r - l + 1 ansL, ansR = l, l + len } if _, ok := ori[s[l]]; ok { cnt[s[l]] -= 1 } l++ } } if ansL == -1 { return "" } return s[ansL:ansR] }